Косой изгиб призматического стержня

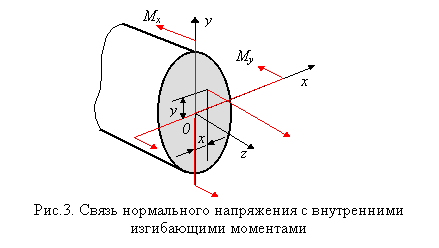
Известно, что косой изгиб имеет место, когда силы, его вызывающие, не лежат в одной из главных плоскостей инерции. Однако, если разложить внешние силы по главным осям инерции Ох и Оу, то получим две системы сил P_1x, P_2x,..., P_nx и P_1y, P_2y,..., P_ny, каждая из которых вызывает прямой изгиб с изгибающими моментами соответственно My и Мx (рис. 2). Применяя принцип независимости действия сил, нормальные напряжения s (рис. 3) определим как алгебраическую сумму напряжений от M_x и М_y:

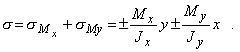
Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу. Прогибы балки определим как геометрическую сумму прогибов от прямых изгибов (рис. 2)

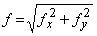
Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений и геометрическим суммированием прогибов.

 

В случае поперечных сечений, имеющих две оси симметрии и выступающие угловые точки (рис. 4) с равными по модулю и максимальными одноименными координатам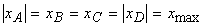и и напряжения в этих точках будут равны

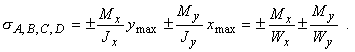
Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис. 5 верхний ряд знаков "+" и "-" соответствует напряжениям от М_x, а нижний ряд - от M_y, и напряжения в этих точках будут равны

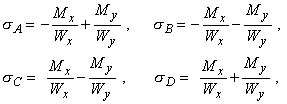
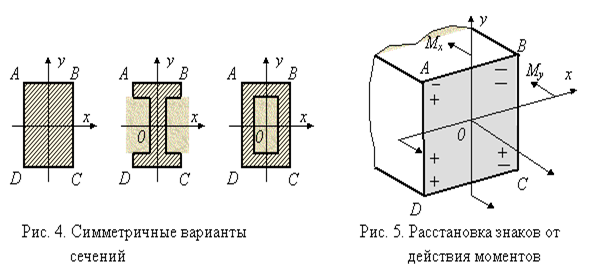
Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде

В остальных случаях для определения max а (или max dp и max | s_c | для хрупкого материала) необходимо по общей формуле проверить напряжения во всех подозрительных точках.

Есть и другой путь: положив s = 0, получим уравнение нейтральной линии. Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то max s будут возникать в наиболее удаленных от нее точках.

18 очетание изгиба и кручения призматического стержня

Ключевые слова: вал, эквивалентный момент, эквивалдентные напряжения, прочность.

Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения (рис. 1).

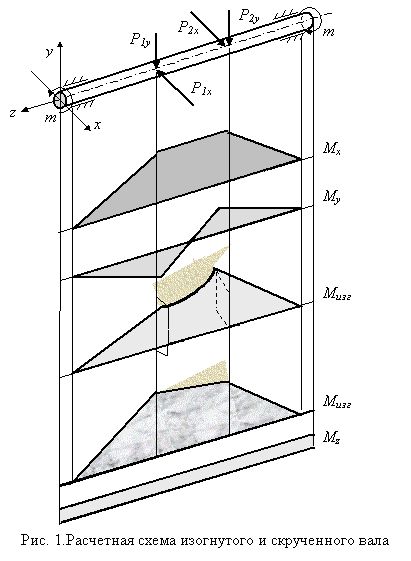
Примем следующий порядок расчета.

1. Разлагаем все внешние силы на составляющие

P_1x, P_2x,..., P_nx и P_1y, P_2y,..., P_ny

2. Строим эпюры изгибающих моментов M _y и M _y. от этих групп сил.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента Mx, и My а целесообразно их заменить результирующим (суммарным) изгибающим моментом

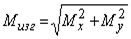
который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси n-n, перпендикулярной вектору М_изг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения прочности равноценны, то обычно эпюру М_изг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

3. Строится эпюра крутящего момента М_z.

Наибольшие напряжения изгиба возникают в точках k и k', наиболее удаленных от нейтральной оси (рис. 3),

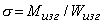
где W_изг - момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

где W_р - момент сопротивления при кручении.

Как следует из рис. 3, напряженное состояние является упрощенным плоским (сочетание одноосного растяжения и чистого сдвига). Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по критерию Треска-Сен-Венана имеем

Учитывая, что W_р=2W_изг, для эквивалентных напряжений получаем

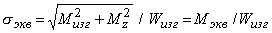
где - эквивалентный момент, с введением которого задача расчета вала на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.

Аналогично для М_экв по критерию Губера-Мизеса получаем

Тогда условие прочности для вала из пластичного материала будет иметь вид

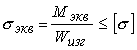
Для стержня из хрупкого материала условие прочности следует записать в виде

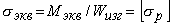
где М_экв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора

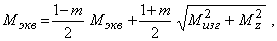
где m = [s_p] / [s_c].

Обратим внимание на особенности расчета при сочетании изгиба, растяжения и кручения стержня прямоугольного поперечного сечения (рис. 4). Для выявления опасной точки здесь должны быть сравнены напряжения косого изгиба с растяжением в точке А, с эквивалентными напряжениями в точках В и С.

Полученные соотношения приобретают крайнюю необходимость и востребованность при выполнении Вами курсового проекта по основам конструирования при расчете на прочность и жесткость валов передач.