Содержание
| Введение | |
| 1 Анализ характеристик разрабатываемой схемы и обзор устройств с подобными характеристиками | |
| 2 Синтез принципиальной схемы устройства и описание работы | |
| 3 Описание методики расчета. Расчет параметров элементов схемы, обоснование выбора элементов | |
| Вывод | |
| Перечень использованных литературных источников |
Введение
Фильтрация — преобразование сигналов с целью изменения соотношения между их различными частотными составляющими. Фильтры обеспечивают выделение полезной информации из смеси информационного сигнала с помехой с требуемыми показателями. Основная задача выбора типа фильтра и его расчета заключается в получении таких параметров, которые обеспечивают максимальную вероятность обнаружения информационного сигнала на фоне помех. Частотно-избирательная цепь, выполняющая обработку смеси сигнала и шума некоторым наилучшим образом, называется оптимальным фильтром. Критерием оптимальности принято считать обеспечение максимума отношения сигнал - шум. Это требование приводит к выбору такой формы частотного коэффициента передачи фильтра, которая обеспечивает максимум отношения сигнал-шум на его выходе. В задачах линейной фильтрации предполагается, что наблюдаемый реальный процесс представляет собой аддитивную смесь сигнала и помехи.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно - избирательных фильтров являются фильтры нижних частот (пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (пропускают высокие частоты и задерживают низкие частоты), полосовые фильтры (пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и режекторные фильтры (задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).

Рис. 1. Общее изображение электрического фильтра.
Диапазоны или полосы частот, в которых сигналы проходят, называются полосами пропускания и в них значение амплитудно-частотной характеристики ïH(jw)ç относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задерживания и в них значение амплитудно-частотной характеристики относительно мало, а в идеальном случае равно нулю. В качестве примера на рис. 2 штриховой линией показана амплитудно-частотная характеристика идеального фильтра нижних частот с единственной полосой пропускания 0<w<wc и полосой задерживания w>wc. Частота wc между двумя этими полосами определяется как частота среза. На практике невозможно реализовать эту идеальную характеристику. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной в лаборатории реальной характеристики с заданной степенью точности к идеальной.
В практическом случае полосы пропускания и задерживания четко не разграничены и должны быть формально определены. В качестве полосы пропускания выбирается диапазон частот, где значение амплитудно-частотной характеристики превышает некоторое заранее выбранное число, обозначенное A1 на рис. 2, а полосу задерживания образует диапазон частот, в котором амплитудно-частотная характеристика меньше определенного значения, например, A2. Интервал частот, в котором амплитудно-частотная характеристика постоянно спадает, переходя от полосы пропускания к полосе задерживания, называется переходной областью. Приведенный на рис. 2 пример имеет полосу пропускания 0<w<wc, полосу задерживания w>w1 и переходную область wc<w<w1.
Для частотно-избирательных фильтров наиболее важной является амплитудно-частотная характеристика, поскольку ее значение на некоторой частоте определяет прохождение сигнала этой частоты или его подавление.
По расположению полосы пропускания фильтры делятся на следующие типы:
-фильтры нижних частот (ФНЧ);
-фильтры верхних частот (ФВЧ);
-полосовые фильтры (ПФ);
- заграждающие фильтры (ЗФ);
- гребенчатые фильтры (ГФ), или многополосовые, имеющие несколько полос пропускания.
По наличию активных элементов различают активные фильтры и пассивные.
Активные фильтры способны усиливать проходящие через них сигналы по мощности. На эквивалентной схеме это свойство отражается наличием источника, за счет энергии которого и осуществляется усиление.
Анализ характеристик разрабатываемой схемы и обзор устройств с подобными характеристиками.
По наличию внутренних источников энергии различают:
- фильтры пассивные (RC или LC фильтры)
- фильтры активные (пассивные RC-цепи и активные элементы)
По полосе пропускаемых частот различают:
- фильтры высоких частот (ФВЧ)
- фильтры нижних частот (ФНЧ)
- фильтры полосовые (ПФ)
- фильтры заграждающие / режекторные (ЗФ / РФ)
Если последовательно соединить RC фильтры, то получим полосовой фильтр (рисунок 1).

Рисунок 1. Простейший полосовой RC фильтр
В RC фильтрах конденсатор С, шунтируя сопротивление нагрузки, пропускает сквозь себя самую большую часть переменной составляющей выпрямленного тока.
На рисунке 2 показаны амплитудно-частотные характеристики (АЧХ) фильтров нижних (а), верхних (б) частот, полосового фильтра (в) и заграждающего (г).

Рисунок 2. АЧХ фильтров: а – ФНЧ, б – ФВЧ, в – ПФ, г – ЗФ
(f0 – квазирезонансная частота)
В активных фильтрах используются четыре типа усилителей:
а) инвертирующие с очень большим (теоретически бесконечным) усилением;
б) неинвертирующие с конечным усилением, в частности, с коэффициентом усиления равным единице;
в) инвертирующие с конечным усилением;
г) дифференциальные.
Перечисленные типы усилителей реализуют с помощью интегрированных ОУ, которые сегодня являются практически единственными активными элементами в активных RC фильтрах.
На рисунке 3 приведена схема активного RC фильтра на ОУ с одноконтурной обратной связью. Она состоит из двух пассивных четырёхполюсников А и В и операционного инвертирующего усилителя. Четырёхполюсник А включен между входом фильтра и входом ОУ, а четырёхполюсник В включен в цепи обратной связи между входом и выходом ОУ. Для анализа схем будем считать ОУ идеальным и инвертирующим.

Рисунок 3. Схема активного RC фильтра на ОУ с одноконтурной обратной связью
Активный RC-фильтр с одноконтурной обратной связью в цепи идеального ОУ даёт возможность получать коэффициенты передачи практически с любыми нулями и полюсами.
Одним из ограничений во всех активных фильтрах было минимально возможное количество активных компонентов цепи. Но в современных условиях очень часто является нецелесообразным минимизирование числа активных элементов. Поэтому, если реализация фильтра при большом количестве ОУ может обеспечить более качественные показатели (чем на одном ОУ), предпочтение отдают фильтрам с большим количеством усиливаемых элементов. В таких фильтрах может использоваться два, а чаще три-четыре ОУ. Такие фильтры обозначают буквами KHN по начальным буквам фамилий авторов схемы: Кервина, Хюльсмана, Ньюкомба. Практические схемы активных полосовых фильтров на операционных усилителях строятся самым различным образом. Возможно применение как положительной, так и отрицательной обратной связи.
Для реализации фильтра можно принять схему с одноконтурной отрицательной обратной связью, в которой включен двойной Т-образный мост (рисунок 4).
Элементы С2, С5 и R2, R5 выбираются для такого фильтра попарно равными.
Такая схема позволяет получить высокую добротность, так как мост имеет на резонансной частоте довольно большое сопротивление. Для этого необходимо осуществить точную балансировку моста. Это возможно, если использовать в схеме прецизионные элементы.
Условия баланса моста имеют вид
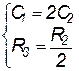 . (1)
. (1)
Обобщенная схема замещения фильтра представлена на рисунке 4.

Рисунок 4 - Схема полосового резонансного фильтра с двойным
Т-образным мостом в цепи ООС

Рисунок 5 - Схема замещения фильтра

Рисунок 6. Схема активного фильтра на трёх ОУ
Чаще всего используют схему, показанную на рисунке 6. В зависимости от используемого выхода, можно получить ФНЧ ил ФВЧ. Относительно ОУ1 фильтр имеет характеристики ФВЧ второго порядка, а относительно ОУ3 – ФНЧ второго порядка.
В качестве RC-цепей для активного полосового фильтра можно использовать:
для четырёхполюсника А



или


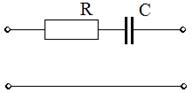
для четырёхполюсника В используют Т-образные мосты



 |
или

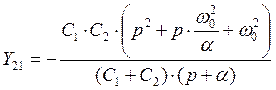


Полосовой фильтр (ПФ) с одноконтурной обратной связью предназначен для выделения сигналов, частота которых лежит в пределах некоторой полосы  . При этом он практически без ослабления пропускает сигналы, лежащие в этой полосе, и ослабляет сигналы, частоты которых лежат за пределами частоты пропускания.
. При этом он практически без ослабления пропускает сигналы, лежащие в этой полосе, и ослабляет сигналы, частоты которых лежат за пределами частоты пропускания.
Полосовые фильтры бывают двухполюсные (второго порядка) и многополюсные (высокого порядка). Передаточная характеристика ПФ второго порядка определяется выражением:
 (2)
(2)
которое имеет два комплексно-сопряженных полюса  и
и  .
.
Затухание фильтра (α) и его добротность (Q) имеют значения
 (3)
(3) 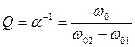 (4)
(4)
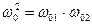 (5)
(5)
Максимальное усиление ПФ в полосе пропускания равно К0 на частоте  . Комплексная амплитудно-частотная характеристика ПФ в соответствии с (1.5) определяется выражением
. Комплексная амплитудно-частотная характеристика ПФ в соответствии с (1.5) определяется выражением
 , (6)
, (6)
откуда получаем значение модуля
 . (7)
. (7)

Рисунок 7.АЧХ полосового фильтра (Q1 > Q2)

Рисунок 8.Пример схемы полосового фильтра
График амплитудно-частотной характеристики ПФ для двух значений добротности (Q1 > Q2) приведён на рисунке 7. С повышением добротности полоса пропускания фильтра сужается, а максимальное усиление остаётся неизменным. Схема ПФ с последовательно соединёнными R и С элементами на входе и Т-образным мостом в цепи обратной связи приведена рисунке 8.
Для такого полосового фильтра:
- максимальное усиление по полосе пропускания К0
 , (8)
, (8)
- частота максимального усиления (квазирезонансная частота) ω0
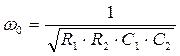 , (9)
, (9)
- добротность фильтра Q
 (10)
(10)
Полосовой фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг центральной частоты fo (Гц) или wo=2πfo (рад/с). На рисунке 9 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты wL и wU представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания wL≤w≤wU и ее ширину BW=wU.- wL
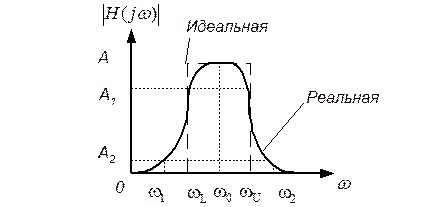
Рисунок 9. Идеальная и реальная амплитудно-частотные характеристики полосового фильтра.
В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определенного значения, например А1 на рисунке 9. Существует также две полосы задерживания 0≤w≤w1 и w≥w2, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, скажем A2. Диапазоны частот между полосами задерживания и полосой пропускания, а именно w1<w<wL и wU<w<w2, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.
Передаточные функции полосовых фильтров можно получить из нормированных функций нижних частот переменной s с помощью преобразования
 (11)
(11)
Отношение Q=wo/BW характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q — относительно широкая ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом K=│H(jwo)│.
В каждом случае центральная частота и частота среза связаны следующим соотношением:
 (12)
(12)
где
 (13)
(13)
Путем последовательного соединения ФНЧ и ФВЧ получаются полосовые фильтры с широкой полосой пропускания. При этом частота среза фильтра нижних частот должна быть выше частоты среза верхних частот и лишь в частном случае эти частоты могут быть взяты равными.
Достоинства полосовых фильтров.
Пассивные фильтры построены из катушек индуктивности, конденсаторов и сопротивлений. Большинство пассивных фильтров для работы в тех диапазонах частот, где они находят применение, нуждаются в больших по размеру, тяжелых и дорогих катушках индуктивности и ослабляют частоты в полосе пропускания, а не только в полосе подавления, хотя частоты в этой последней ослабляются сильнее. Используемые в пассивных фильтрах катушки индуктивности обладают активным сопротивлением, межвитковой ёмкостью и потерями в сердечнике, что делает их свойства далекими от идеальных.
По сравнению с пассивными активные фильтры имеют следующие преимущества:
1) в них используются только сопротивления и конденсаторы, т.е. компоненты, свойства которых ближе к идеальным, чем свойства катушек индуктивности;
2) относительно дешевы;
3) они могут обеспечивать усиление в полосе пропускания и редко вносят существенные потери;
4) использование в активных фильтрах операционных усилителей обеспечивает развязку входа от выхода (поэтому активные фильтры легко делать многокаскадными и тем самым улучшать их показатели);
5) активные фильтры относительно легко настраивать;
6) фильтры для очень низких частот могут быть построены из компонентов, имеющих умеренные значения параметров;
7) активные фильтры невелики по размерам и массе.
Недостатки полосовых фильтров
Они нуждаются в источнике питания, а их рабочий диапазон частот ограничен сверху максимальной рабочей частотой операционного усилителя. Это приводит к тому, что большинство активных фильтров может работать лишь на частотах, не превышающих нескольких мегагерц, хотя отдельные типы операционных усилителей могут обеспечить работу фильтров и на более высоких частотах. По мере улучшения изготовителями операционных усилителей их частотных характеристик будет увеличиваться и верхний частотный предел активных фильтров.






