Рассмотрим изгиб пластинки нагруженной поперечной силой, которая свободно опирается по контуру, то есть опорные реакции на краях должны быть нормальны к пластинке. Прогибы при этом примем малыми в сравнении с толщиной. При этих условиях можно пренебречь деформацией в срединной плоскости пластины.
Рассмотрим элемент, вырезанный из пластинки, как показано на рис.4.

|
Кроме изгибающих и крутящих моментов, в данном случае будут еще и вертикальные перерезывающие силы, приложенные по боковым граням элемента
 . (6)
. (6)
Так как моменты и перерезывающие силы являются функциями координат х и у, то при исследовании условий равновесия элемента мы должны будем принять во внимание малые изменения этих величин, обусловленные изменениями координат на малые величины dx и dy.
Срединная плоскость элемента представлена на рис.5, где указаны те направления сил и моментов, которые принимаются положительными.
|


Если нагрузка распределена по верхней поверхности пластинки, то интенсивность такой нагрузки q, или действующая на элемент поверхности q d x d y.
Проектируя все приложенные к элементу силы на ось z, получим следующее уравнение равновесия:
 ,
,
из которого
 , (7)
, (7)
Взяв моменты от всех действующих на элемент сил относительно оси х, получим другое уравнение равновесия
 . (8)
. (8)
Моментом нагрузки q и моментом, возникающим вследствие изменения силы  , пренебрегаем ввиду того, что они представляют собой величины более высокого порядка малости. Тогда после упрощений уравнение равновесия (8) принимает вид
, пренебрегаем ввиду того, что они представляют собой величины более высокого порядка малости. Тогда после упрощений уравнение равновесия (8) принимает вид
относительно оси х
 , (9)
, (9)
относительно оси у
 . (10)
. (10)
Так как в направлениях х и у сил нет, а относительно оси z нет моментов, то три уравнения (7), (9) и (10) полностью определяют равновесие элемента. Исключим из этих уравнений перерезывающие силы 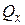 и
и  , определив их из уравнений (9), (10) и произведя подстановку их значений в уравнение (7) получим
, определив их из уравнений (9), (10) и произведя подстановку их значений в уравнение (7) получим
 . (11)
. (11)
С учетом  , вследствие того, что
, вследствие того, что  , представим уравнение равновесия (11) в окончательной форме:
, представим уравнение равновесия (11) в окончательной форме:
 . (12)
. (12)
Для определения зависимости изгибающих моментов от функции прогибов рассмотрим чистый изгиб пластинки (рис.6).
|
Выделим из пластинки элемент, как показано на рис.7. Пусть  и
и  обозначают кривизны этой нейтральной поверхности в сечениях, параллельных соответственно плоскостям xz и yz. В таком случае, как и для балки, мы можем найти относительные удлинения в направлениях x и y для элементарного слоя abcd, отстоящего от нейтрального слоя на расстояние z; они будут равны.
обозначают кривизны этой нейтральной поверхности в сечениях, параллельных соответственно плоскостям xz и yz. В таком случае, как и для балки, мы можем найти относительные удлинения в направлениях x и y для элементарного слоя abcd, отстоящего от нейтрального слоя на расстояние z; они будут равны.
 ,
,  . (13)
. (13)
 |
С учетом закона Гука (1) находим соответствующие напряжения в слое abcd
 (14)
(14)
Эти напряжения пропорциональны расстоянию  слоя abcd от нейтральной поверхности и зависят от величины кривизны изогнутой пластинки.
слоя abcd от нейтральной поверхности и зависят от величины кривизны изогнутой пластинки.
Так как эти нормальные растяжения распределены по боковым граням показанного на рис.7 элемента, то их можно привести к парам, величины которых, приходящиеся на единицу длины, должны быть, очевидно, равны внешним моментам  и
и  . Таким путем получаем уравнения
. Таким путем получаем уравнения
 (15)
(15)
Подставив в них вместо  и
и  выражение (14), получим соотношения для определения моментов
выражение (14), получим соотношения для определения моментов
 (16)
(16)
 . (17)
. (17)
Отметим, что в следствии малой толщины в сравнении с размерами пластинки пренебрегаем влиянием на изгиб перерезывающих сил 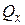 и
и  и сжимающего напряжения
и сжимающего напряжения 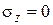 , вызванного нагрузкой q.
, вызванного нагрузкой q.
Подставляя эти выражения (16), (17) в уравнение (12) найдем дифференциальное уравнение изогнутой поверхности
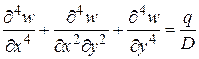 (18)
(18)
или в символической форме
 . (19)
. (19)
Это уравнение (18) было представлено Лагранжем в 19811г., когда он рассматривал доклад, представленный во Французскую Академию наук Софией Жермен.
Уравнениями (9), (10) воспользуемся для определения перерезывающих сил
 , (20)
, (20)
 , (21)
, (21)
Компоненты тензора напряжений при изгибе определяются
 , (22)
, (22)
или с учетом закона Гука 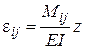 , (23)
, (23)
где 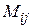 – изгибающий момент (рис.8);
– изгибающий момент (рис.8);  – момент инерции; z – расстояние до срединной поверхности. Тогда максимальные напряжения определяются в виде
– момент инерции; z – расстояние до срединной поверхности. Тогда максимальные напряжения определяются в виде
 , (24)
, (24)
в декартовой системе координат
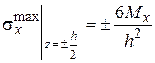 ,
,  , (25)
, (25)
 | |||
| |||
В случае действия касательных напряжений  сдвиговые деформации определяются как
сдвиговые деформации определяются как
 , (26)
, (26)
где G – модуль сдвига.
Максимальные касательные напряжения имеют вид:
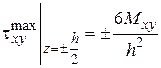 , (27)
, (27)
Для определения напряжений 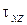 и
и 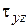 , предположим, что они распределены по толщине пластинки по параболическому закону. Тогда
, предположим, что они распределены по толщине пластинки по параболическому закону. Тогда
 ,
,  . (28)
. (28)
Таким образом, задача об изгибе пластинки поперечной нагрузкой сводится к интегрированию Уравнения Софии Жермен (18). Если для какого-либо частного случая решение этого уравнения найдено и оно удовлетворяет граничным условиям, то с учетом выражений (16), (17) для определения моментов могут быть вычислены нормальные и касательные напряжения, а также деформации
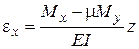 ;
;  ;
;  , (29)
, (29)
то есть определить напряженно деформированное состояние пластинки, которая находится под поперечной нагрузкой.
Деформации также можно выразить через моменты
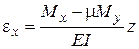 ;
;  ;
;  . (30)
. (30)
Кривизны в осевых направлениях
 ,
,  ,
,  , (31)
, (31)
где  – радиусы кривизны в соответствующих направлениях.
– радиусы кривизны в соответствующих направлениях.
Изгиб круглых пластин
 При изгибе круглой пластинки (рис.9) решение необходимо вести в цилиндрических координатах. Если начало координат поместить в центре не изогнутой пластинки, через r обозначим радиальные расстояния точек, лежащих в срединной плоскости. Тогда максимальный наклон изогнутой поверхности в некоторой точке А будет равен
При изгибе круглой пластинки (рис.9) решение необходимо вести в цилиндрических координатах. Если начало координат поместить в центре не изогнутой пластинки, через r обозначим радиальные расстояния точек, лежащих в срединной плоскости. Тогда максимальный наклон изогнутой поверхности в некоторой точке А будет равен 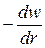 , кривизна же срединной поверхности пластинки в диаметральном сечении rz для малых прогибов выразится производной
, кривизна же срединной поверхности пластинки в диаметральном сечении rz для малых прогибов выразится производной
 , (32)
, (32)
где  – малый угол между нормалью к изогнутой поверхности в точке А и осью симметрии ОВ. Из условий симметрии заключаем, что
– малый угол между нормалью к изогнутой поверхности в точке А и осью симметрии ОВ. Из условий симметрии заключаем, что  представляет собой одну из главных кривизн изогнутой поверхности в точке А. Вторая главная кривизна лежит в сечении, проходящем через нормаль АВ и перпендикуляр к плоскости rz. заметив, что подобные АВ нормали для всех остальных точек срединной поверхности с радиальным расстоянием r образуют в своей совокупности коническую поверхность с вершиной в В, очевидно, что расстояние АВ представляет собой радиус кривизны, который мы обозначим через
представляет собой одну из главных кривизн изогнутой поверхности в точке А. Вторая главная кривизна лежит в сечении, проходящем через нормаль АВ и перпендикуляр к плоскости rz. заметив, что подобные АВ нормали для всех остальных точек срединной поверхности с радиальным расстоянием r образуют в своей совокупности коническую поверхность с вершиной в В, очевидно, что расстояние АВ представляет собой радиус кривизны, который мы обозначим через  . тогда из чертежа получим
. тогда из чертежа получим
 . (33)
. (33)
Имея выражения (32) и (33) для главных кривизн, мы можем получить и соответствующие значения изгибающих моментов, полагая, что между этими моментами и кривизнами остаются в силе соотношения (16), которые выведены в предположении незначительного влияния касательных напряжений на величину прогибов. Пользуясь этими соотношениями, получаем изгибающие моменты по окружным (тангенциальным) сечениям пластинки и диаметральному сечению rz.
 , (34)
, (34)

 . (35)
. (35)
Уравнения (34) и (35) содержат лишь одну переменную из двух, которая может быть определена из условий равновесия элемента пластинки, аналогичного, например, элементу abcd на рис.10, вырезанному из пластинки двумя цилиндрическими сечениями ab и cd и двумя диаметральными ad и bc.
Например, пара, действующая по грани cd элемента, равна

 (36)
(36)
соответствующая пара по грани ab выразится произведением
 . (37)
. (37)
Каждая из пар, приложенных по граням ad и bc элемента, равна 
 обе же вместе они дадут равнодействующую пару в плоскости rOz, равную
обе же вместе они дадут равнодействующую пару в плоскости rOz, равную

 . (38)
. (38)
Полная перерезывающая сила, действующая по грани cd элемента, будет  ; соответствующая же сила по грани ab равна
; соответствующая же сила по грани ab равна
 . (39)
. (39)
Пренебрегая малой разностью между перерезывающими силами по двум противоположным граням элемента, мы вправе утверждать, что эти силы дают пару в плоскости rz, равную
 . (40)
. (40)
Складывая с надлежащими знаками моменты (36), (37), (38), (40) и пренебрегая моментом от приходящейся на элемент внешней нагрузки, как малой величиной более высокого порядка, получим для элемента abcd следующее уравнение равновесия:
 ,
,
из которого, пренебрегая малой величиной более высокого порядка, находим
 . (41)
. (41)
Если вместо 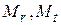 подставив сюда их выражения (34), (35), то уравнение (41) примет вид
подставив сюда их выражения (34), (35), то уравнение (41) примет вид
 (42)
(42)
или в другом виде
 . (43)
. (43)
В любом частном случае симметрично нагруженной круглой пластинки перерезывающая сила легко может быть вычислена путем деления распределенной по окружности радиуса r нагрузки на  . Тогда уравнениями (42) и (43) можно будет воспользоваться для определения наклона
. Тогда уравнениями (42) и (43) можно будет воспользоваться для определения наклона  и прогиба
и прогиба  пластинки. интегрирование этих уравнений упрощается, если мы заметим, что их можно представить следующим образом:
пластинки. интегрирование этих уравнений упрощается, если мы заметим, что их можно представить следующим образом:
 , (44)
, (44)
 . (45)
. (45)
В случае если, например, пластинка нагружена равномерно распределенной по поверхности нагрузкой инесивностью q, то величина перерезывающей силы Q на расстоянии r от центра пластинки определяется из уравнения
 ,
,  .
.
Таким образом, если  представлена в функции r, то уравнения (44), (45) без всяких затруднений можно будет проинтегрировать в любом частном случае, а постоянные интегрирования найти из граничных условий.
представлена в функции r, то уравнения (44), (45) без всяких затруднений можно будет проинтегрировать в любом частном случае, а постоянные интегрирования найти из граничных условий.
Граничные условия
1. В случае, когда край пластинки защемлен (рис.11) прогиб по этому краю равен нулю и плоскость, касательная к изогнутой срединной поверхности, совпадает на нем с начальным положением срединной плоскости пластинки (угол поворота равен нулю). Тогда граничные условия имеют вид

 . (46)
. (46)
2. Если край пластинки свободно оперт (рис.12), то его прогиб должен быть равен нулю. В то же время этот край может свободно поворачиваться относительно оси х; это значит, что изгибающие моменты  обращаются на нем в нуль
обращаются на нем в нуль

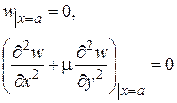 . (47)
. (47)
Также наряду с этим обращается в нуль  , поэтому уравнения (47) можно считать эквивалентным уравнениям
, поэтому уравнения (47) можно считать эквивалентным уравнениям
 , (48)
, (48)
не содержащим коэффициента Пуассона 
3. В том случае, край пластинки совершенно свободен (рис.13), то естественно принять, что поэтому краю нет ни изгибающих или крутящих моменнтов, ни вертикальных перерезывающих сил

 ,
,
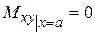 , (49)
, (49)
 .
.
В этой форме граничные условия для свободного края были выражены Пуассоном. Позднее Кирхгофф доказал, что трех условий слишком много и что для полного определения удовлетворяющих дифференциальному уравнению С. Жермен прогибов достаточно двух условий. На этом основании объединенное требование относительно крутящего момента  и перерезывающей силы
и перерезывающей силы 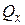 для свободного края принимает вид
для свободного края принимает вид
 (50)
(50)
подставив сюда вместо 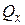 и
и  их выражения (20) и (17), получаем окончательно для свободного края
их выражения (20) и (17), получаем окончательно для свободного края  :
:
 . (51)
. (51)
Условие, чтобы изгибающие моменты на свободном крае были равны нулю, требует
 . (52)
. (52)
Уравнения (51) и (52) представляют собой два необходимых граничных условия для свободного края пластинки.
.
Применение энергетических методов к расчету пластин.
Примеры решения задач
В тех случаях, когда точное решение задач по определению напряжений и деформаций в пластинках невозможно, прибегают к приближенным методам.
Одними из них являются вариационные, они дают приближенное аналитическое выражение для искомой функции.
Это – метод Ритца, метод Галеркина, метод Треффца, метод Канторовича.
Вариационные методы базируются на экспериментальных свойствах потенциальной энергии.
Определение: Потенциальной энергией упругой системы называется та работа, которую совершают как внутренние, так и внешние силы системы, при переводе её из деформированного состояния в начальное состояние - недеформированное.
Э = U + V
Э – полная энергия системы; U – потенциальная энергия внутренних сил, линейно зависящих от деформации. Всегда положительна и вычисляется как половина произведения сил на соответствующие перемещения; V – потенциальная энергия внешних сил.
Потенциальная энергия работы внешних сил всегда отрицательна и определяется как полная величина произведения силы на путь:
V = –A н
где А н – работа внешних сил.
Потенциальная энергия действительного состояния системы имеет экстремальное значение, математически это можно записать следующим образом:
δЭ = 0
Потенциальная энергия в состоянии равновесия минимальна, т.е.:
δ2 Э > 0
Для решения согласно методу Ритца, необходимо найти такую функции прогиба ω(x), которая будет сообщать минимум функционалу
 ,
,
Если задать функцию ω(x) в виде ряда
 ,
,

где  – неопределенные параметры;
– неопределенные параметры;  – подходящие функции, удовлетворяющие граничным условиям задачи
– подходящие функции, удовлетворяющие граничным условиям задачи
и подставить её в функционал J, мы получим функцию от неизвестных параметров  .
.
После определения производных

из системы n уравнений находим определяющие коэффициенты  .
.
Потенциальная энергия пластинки
Потенциальная энергия пластинки  , в общем случае, выражается через перемещения:
, в общем случае, выражается через перемещения:

 (1)
(1)
где ω(x, y) – функция прогибов. Основная задача расчетов пластин – определение прогибов, т.к. по известным прогибам можно рассчитать напряжения в пластине и возникающие моменты.
Наиболее удобной формой выражения функции ω(x,y) – аппроксимирующей функции, является представление функции в виде ряда:
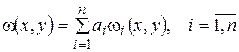
где  - удовлетворяющие граничным условиям функции, т.е. геометрическим условиям задачи.
- удовлетворяющие граничным условиям функции, т.е. геометрическим условиям задачи.
Пример

Рассмотрим изгиб свободно опертой прямоугольной пластинки, нагруженной равномерно распределенной по поверхности нагрузкой p = const.
 Задача:
Задача:
Выберем функцию прогибов, удовлетворяющую граничным условиям в виде тригонометрического ряда, ограничимся первым членом ряда

Найти
Определить вид прогибов и их максимальные значения
Решение
Функция удовлетворяет граничным условиям свободного закрепления пластинки:

а) Прогибы в местах закрепления равны нулю:

б) Изгибающие моменты на краях закрепления равны нулю:

В уравнении (1), D – цилиндрическая жесткость пластинки:
 ,
,
где Е – модуль упругости; μ – коэффициент Пуассона; h – толщина пластинки;
Находим производные:



Подставляем в уравнение (1), получаем:

 (2)
(2)
Интегрируем выражение (2) с учетом:

Получим:
 ;
;
Находим параметр а 1 из условия, что:
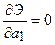
Получим:
 ,
,
Тогда:

очевидно, что максимальные прогибы будут в центре пластинки ( ), тогда
), тогда
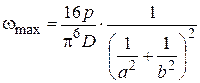 .
.


рис. 1
=================================================
Указания:
В решении необходимо учитывать:


ЛАБОРАТОРНАЯ РАБОТА № 1





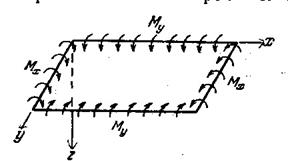 Рис.6
Рис.6

