Три точки  ,
,  ,
,  лежат на одной прямой тогда и только тогда, когда определитель
лежат на одной прямой тогда и только тогда, когда определитель
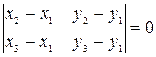 . .
| (13) |
Равенство нулю определителя (13) означает, что площадь «треугольника» 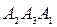 равна нулю.
равна нулю.
Взаимное расположение прямой и пары точек
Пусть заданы точки 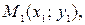
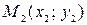 и общее уравнение некоторой прямой: Ax + By + C = 0. Вычислим значения величин
и общее уравнение некоторой прямой: Ax + By + C = 0. Вычислим значения величин 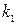 и
и  по формулам:
по формулам:

| (14) | 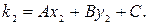
| (15) |
Взаимное расположение точек  и
и 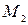 относительно заданной прямой можно определить по следующим признакам:
относительно заданной прямой можно определить по следующим признакам:
1) числа 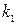 и
и  имеют одинаковые знаки, в этом случае точки
имеют одинаковые знаки, в этом случае точки 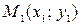 и
и 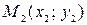 лежат по одну сторону от прямой;
лежат по одну сторону от прямой;
2) числа 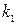 и
и  имеют противоположные знаки, в этом случае точки
имеют противоположные знаки, в этом случае точки  и
и 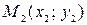 лежат по разные стороны от прямой;
лежат по разные стороны от прямой;
3) одно из чисел 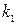 ,
,  равно нулю (или оба равны нулю), в этом случае точка
равно нулю (или оба равны нулю), в этом случае точка  или
или 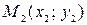 соответственно (или обе) принадлежит прямой.
соответственно (или обе) принадлежит прямой.
Расстояние от точки до прямой
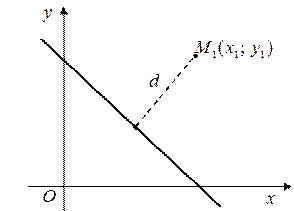 Рис. 5
Рис. 5
| Расстояние d от точки 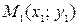 до прямой Ax + By + C = 0 (рис. 5) вычисляется по формуле: до прямой Ax + By + C = 0 (рис. 5) вычисляется по формуле:
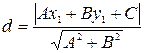 . (16) . (16)
|
Пучок прямых
Через одну фиксированную точку  (рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком (пучком) прямых, а точка
(рис. 6) на плоскости можно провести бесконечное множество прямых. Это множество называется цент-ральным пучком (пучком) прямых, а точка  называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
называется центром пучка. Каждую из прямых пучка (кроме той, которая параллельна оси
ординат) можно представить уравнением:

| (17) |
где  tg tg  – угловой коэффициент прямой (см. рис. 6).
Уравнение вида (17) называется уравнением пучка прямых с центром в точке – угловой коэффициент прямой (см. рис. 6).
Уравнение вида (17) называется уравнением пучка прямых с центром в точке 
|  Рис. 6
Рис. 6
|
Угол между прямыми
Если пара прямых на плоскости задана общими уравнениями:  (рис. 7, прямая f) и (рис. 7, прямая f) и 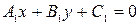 (рис. 7, прямая g), то косинус угла между этими прямыми может быть вычислен по формуле: (рис. 7, прямая g), то косинус угла между этими прямыми может быть вычислен по формуле:
|  Рис. 7
Рис. 7
|
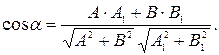
| (18) |
Если пара прямых на плоскости задана уравнениями «с угловым коэффициентом»: 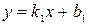 и
и 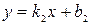 , то тангенс угла между этими прямыми рассчитывается по уравнению:
, то тангенс угла между этими прямыми рассчитывается по уравнению:
tg 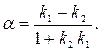
| (19) |
Если пара прямых на плоскости задана своими каноническими уравнениями: 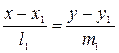 и
и 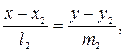 то косинус угла между этими прямыми определяется по формуле:
то косинус угла между этими прямыми определяется по формуле:

| (20) |
Условия параллельности и перпендикулярности прямых
Прямые, заданные общими уравнениями: 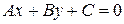 и
и 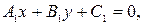 взаимно перпендикулярны тогда и только тогда, когда
взаимно перпендикулярны тогда и только тогда, когда  Данные прямые параллельны тогда и только тогда, когда
Данные прямые параллельны тогда и только тогда, когда 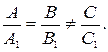
Прямые на плоскости, заданные в виде: 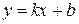 и
и 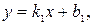 перпендикулярны только том случае, когда
перпендикулярны только том случае, когда 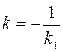 (при
(при  ). Данные прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т. е.
). Данные прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны, т. е. 
Прямые, заданные своими каноническими уравнениями: 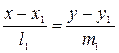 и
и 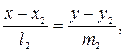 взаимно перпендикулярны тогда и только тогда, когда
взаимно перпендикулярны тогда и только тогда, когда  Данные прямые параллельны, если только выполнено условие:
Данные прямые параллельны, если только выполнено условие: 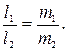
Точка пересечения непараллельных прямых
Если на плоскости заданы две прямые:  и
и 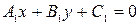 , то согласно утверждению 2 координаты
, то согласно утверждению 2 координаты 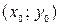 точки пересечения этих прямых можно вычислить по формулам:
точки пересечения этих прямых можно вычислить по формулам:

| (21) | 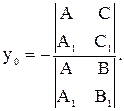
| (22) |
1. ТИПЫ КРИВЫХ ВТОРОГО ПОРЯДКА
Основные понятия
Кривой второго порядка называется линия, имеющая в некоторой декартовой системе координат уравнение второй степени относительно x и y
 , ,
| (1) |
где 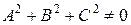 .
.
Можно показать, что уравнение (1) может задавать только эллипс, параболу или гиперболу. Остальные случаи будем называть вырожденными. Ниже рассмотрим подробнее все перечисленные типы кривых второго порядка.
Эллипс
Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.
Обозначим фокусы эллипса через F 1 и F 2, расстояние между ними назовем фокусным расстоянием и обозначим 2 c, а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокуса, через 2 a (по условию  ).
).
Введем декартову систему координат так, чтобы фокусы F 1 и F 2 оказались на оси абсцисс, а начало координат совпало с серединой отрезка F 1 F 2. В выбранной таким образом системе координат левый фокус имеет координаты  , а правый – , а правый –  (рис. 1) (рис. 1)
|  Рис. 1 Рис. 1
|
Пусть  – произвольная точка эллипса. По определению сумма расстояний от этой точки до фокусов равна 2 a. Исходя из этого факта и введя обозначение
– произвольная точка эллипса. По определению сумма расстояний от этой точки до фокусов равна 2 a. Исходя из этого факта и введя обозначение 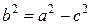 , получим уравнение эллипса:
, получим уравнение эллипса:

| (2) |
Оно называется каноническим уравнением эллипса. Здесь a и b – большая и малая полуоси эллипса. Оси координат будут являться также осями симметрии эллипса.
В описанном выше случае  . Если фокусы F 1 и F 2 располагаются на оси ординат симметрично относительно начала координат, т.е. имеют координаты . Если фокусы F 1 и F 2 располагаются на оси ординат симметрично относительно начала координат, т.е. имеют координаты  и и 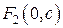 , то обозначив сумму расстояний от любой точки эллипса до фокусов 2 b и введя , то обозначив сумму расстояний от любой точки эллипса до фокусов 2 b и введя 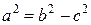 , вновь получим уравнение (2), но при этом , вновь получим уравнение (2), но при этом  (рис. 2)
Точка (рис. 2)
Точка 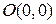 называется центром, а точки с координатами называется центром, а точки с координатами 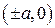 и и  – вершинами эллипса. – вершинами эллипса.
| 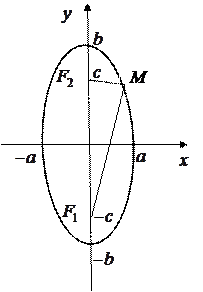 Рис. 2 Рис. 2
|
Отношение величины расстояния между фокусами к длине большей оси называется эксцентриситетом эллипса и обозначается e.

| (3а) | или | 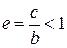
| (3б) |
Отсюда и возникло название кривой: в переводе с греческого эллипс означает «недостаток».
При построении эллипс вписывают в «опорный» прямоугольник, т.е прямоугольник с центром в начале координат и длинами сторон 2 a и2 b.
В случае равенства осей 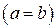 уравнение принимает вид
уравнение принимает вид

| (4) |
и мы получаем частный случай эллипса – окружность. У окружности расстояние между фокусами равно нулю  , оба фокуса при этом совпадают с центром окружности.
, оба фокуса при этом совпадают с центром окружности.
Обычно для построения эллипса на осях координат откладывают полуоси и строят прямоугольник со сторонами, параллельными осям координат. При этом длины сторон 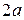 и
и  , а серединами сторон являются точки
, а серединами сторон являются точки 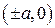 и
и 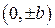 . Затем в полученный прямоугольник вписывают эллипс.
. Затем в полученный прямоугольник вписывают эллипс.
Гипербола
Гиперболой называется геометрическое место точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Введем декартову систему координат аналогично случаю, описанному выше для эллипса, т.е. фокусы имеют координаты  и
и  (рис. 3). Каноническое уравнение гиперболы в этом случае будет иметь вид:
(рис. 3). Каноническое уравнение гиперболы в этом случае будет иметь вид:
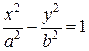
| (5) |

Рис. 3
Здесь  или
или 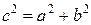 . При этом a называется действительной, а b – мнимой полуосью гиперболы.
. При этом a называется действительной, а b – мнимой полуосью гиперболы.
При  гипербола называется равнобочной.
гипербола называется равнобочной.
Если же декартова система координат выбрана таким образом, что фокусы имеют координаты  и
и 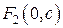 (рис.4), то каноническое уравнение гиперболы принимает вид:
(рис.4), то каноническое уравнение гиперболы принимает вид:

| (6) |
В этом случае b называется действительно полуосью, а a – мнимой.
Объединив формулы (5) и (6), получим каноническое уравнение гиперболы в виде:
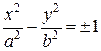
| (7) |
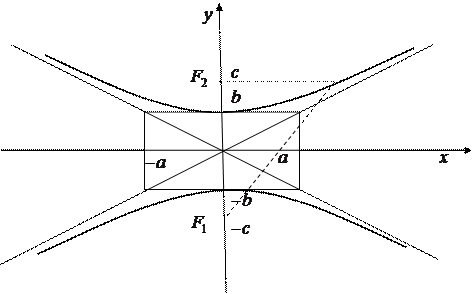 Рис. 4
Рис. 4
Как и в случае с эллипсом, координатные оси являются осями симметрии, а точка 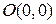 – центром симметрии гиперболы. Прямые
– центром симметрии гиперболы. Прямые 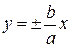 обладают следующим свойством: точки гиперболы при удалении от начала координат (при
обладают следующим свойством: точки гиперболы при удалении от начала координат (при  ) подходят сколь угодно близко к этим прямым. Прямые с таким свойством называются асимптотами.
) подходят сколь угодно близко к этим прямым. Прямые с таким свойством называются асимптотами.
Точка 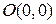 называется центром гиперболы. Точки с координатами
называется центром гиперболы. Точки с координатами 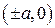 в случае, описанномуравнением (5), и точки с координатами
в случае, описанномуравнением (5), и точки с координатами  в случае, описанномуравнением (6), называются вершинами гиперболы.
в случае, описанномуравнением (6), называются вершинами гиперболы.
Отношение величины расстояния между фокусами к длине действительной полуоси называется эксцентриситетом гиперболы

| (8а) | или | 
| (8б) |
Отсюда и возникло название кривой: в переводе с греческого гипербола означает «избыток».
Для построения гиперболы сначала строим опорный прямоугольник со сторонами длины 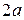 и
и  , параллельными осям координат, и серединами сторон
, параллельными осям координат, и серединами сторон 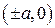 и
и 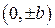 . Каждая из двух ветвей гиперболы вписана в бесконечную область, ограниченную продолжением диагоналей опорного прямоугольника и парой его сторон. Положение ветвей определяется знаком в правой части уравнения (7): если он отрицательный, то ветви вписаны в верхнюю и нижнюю область (вершины – точки
. Каждая из двух ветвей гиперболы вписана в бесконечную область, ограниченную продолжением диагоналей опорного прямоугольника и парой его сторон. Положение ветвей определяется знаком в правой части уравнения (7): если он отрицательный, то ветви вписаны в верхнюю и нижнюю область (вершины – точки 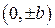 ); если же положительный, то в правую и левую (соответственно вершинами являются точки
); если же положительный, то в правую и левую (соответственно вершинами являются точки 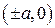 ).
).
Парабола
Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.
Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Пусть фокус имеет координаты  , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 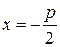 . Тогда уравнение параболы запишется в виде:
. Тогда уравнение параболы запишется в виде:
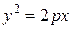
| (9) |
Данное уравнение называется каноническим уравнением параболы. Ось абсцисс будет являться осью симметрии параболы, заданной уравнением (9). При  все точки такой параболы располагаются в правой полуплоскости (рис. 5), а при все точки такой параболы располагаются в правой полуплоскости (рис. 5), а при  – в правой. – в правой.
| 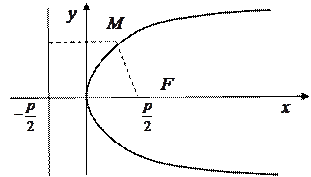 Рис. 5
Рис. 5
|
Если же мы поместим фокус на оси ординат, т.е. он будет иметь координаты 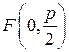 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид  , то канонической уравнение параболы выглядит так:
, то канонической уравнение параболы выглядит так:

| (10) |
Для параболы, заданной уравнением (10), осью симметрии является ось ординат. При  все точки такой параболы располагаются в верхней полуплоскости, а при все точки такой параболы располагаются в верхней полуплоскости, а при  – в нижней. – в нижней.
|
 Рис. 6 Рис. 6
|
2. ПРИВЕДЕНИЕ УРАВНЕНИЙ КРИВЫХ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ КООРДИНАТ






