Ціль:
• Аналіз роботи схем для моделювання операцій множення.
• Аналіз роботи схем для моделювання операцій розподілу.
З наявних у програмі EWB бібліотечних компонентів у якості універсального функціонального перетворювача, за допомогою якого можна моделювати операції множення й розподілу, може бути використане кероване поліноміальне джерело (надалі - блок), вихідний сигнал якого описується поліномом наступного виду
Y=A+B*V1+C*V2+D*V3+E(V1)2+F*V1*V2+G*V1*V3+H(V2)2+I*V2*V3+J(V3)2+K*V1*V2*V3
Коефіцієнти полінома А...До задаються за допомогою діалогового вікна. Наприклад, для випадку перетворювача із квадратичною передатною характеристикою, схема якого показана на мал. 1, параметри діалогового вікна мають значення, наведені на мал. 2
Як треба з мал. 1, джерело вхідного сигналу підключений до входу 1 перетворювача, тобто у вищенаведеній формулі Vl=Ui. У такому випадку на підставі дані вікна (мал. 2) вираження для вихідної напруги моделі може бути записане в наступному виді:
U0=A+(Ui)2
Постійна А в діалоговому вікні задається у вольтах, вхідна напруга (див. лицьову панель генератора на мал. 1)
Ui=2sinωt
З огляду на відоме із тригонометрії вираження
sin2ά=0,5(1-cos2ά)
U0+4-2cosωt
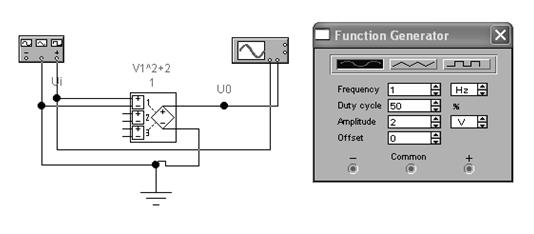
Рис.1.

Рис.2.
Результати моделювання розглянутого перетворювача показані на мал. 3, звідки видно, що на виході перетворювача дійсно формується сигнал відповідно до вираження.
Передатна характеристика перетворювача (мал. 4) дійсно має квадратичний характер, однак її зображення перекручене. Перекручування носять гістерезисний характер і порозуміваються тремтінням фази коливань функціонального генератора, оскільки формування передатної характеристики відбувається протягом декількох періодів його коливань.

Рис3.

Рис.4
Розглянемо перетворювач із кубічною передатною характеристикою (мал. 5 а). Перетворювач містить два поліноміальних блоки Р1 і Р2. У першому блоці реалізується розглянута вище квадратична функція (при А=0), а в другому - функція перемножування вхідного сигналу Ui і вихідного сигналу першого блоку (для Р2 обране А=0 й F=1, див. мал. 2). Таким чином, для цього перетворювача Uo=(Ui)^3. Передатна характеристика перетворювача показана на мал. 5 б.
Таким чином, на базі керованого поліноміального джерела напруги (блоку) можна створювати різноманітні функціональні перетворювачі для моделювання елементів систем автоматичного керування (на жаль, їх не можна вбудовувати в реальні системи).
a)
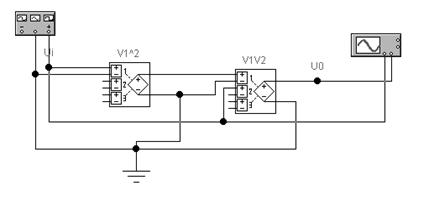
b)

Рис.5.
Хід роботи.
1. Змоделюйте за допомогою керованого поліноміального джерела наступні залежності:
· Y=5*x+2x^2-x^3
· Y=x1^2-x2^2
· Y=2*(x1+3*x2)
2. Внесіть до протоколу результати моделювання:
· Схеми;
· Властивості поліноміальних джерел;
· Передатні характеристики.






