Если представить ствол дерева, выросший в насаждении, рассеченным по сердцевине вертикальной плоскостью, то в сечении получится фигура, ограниченная некоторой кривой, которая определяет и форму, и объем древесного ствола. На поперечных разрезах, она располагается симметрично по отношению к вертикальной оси дерева. Но обычно под влиянием многообразных факторов кривая — «образующая» — древесного ствола сильно варьирует даже в пределах одной древесной породы, и лишь на основе изучения большого экспериментального материала достоверно выявляется представление о некоторой средней ее форме.
Результаты исследований таксаторов в области формы стволов лесных деревьев дают возможность:
· представить ее в виде форм правильных стереометрических тел вращения, полных и усеченных;
· объяснить ее особенности на основе законов физики и механики;
· установить вид математического аналога «образующей» древесного ствола;
Использование законов механики и физики для объяснения формы древесного ствола нашло отражение в исследованиях Метцгера, Козицына П. Д., Гогенадля и др. По гипотезе Метцгера (1898) и Козицына П. Д. (1909) формирование древесного ствола происходит согласно законам строительной механики, и дерево должно противостоять опрокидывающей силе ветра, направленной на точку приложения силы в центре кроны. Отсюда, по заключению Метцгера, кубы диаметров стволов, замеренных на различном расстоянии от точки приложения силы, должны быть пропорциональны расстоянию до точки приложения опрокидывающей силы.
Гогенадль предположил, что главным фактором, обусловливающим форму стволов, является их собственный вес и вес кроны, а не изгибающая сила ветра, т. е. ствол должен быть телом равного сопротивления раздавливанию своим весом. На основе такого заключения Гогенадль пришел к выводу, что образующая древесного ствола должна быть логарифмической кривой и выражена в общем виде равенством: D2 = Aef(x), где
А — постоянный коэффициент, различный для отдельных пород;
е — основание натуральных логарифмов (2,71828);
f(x) — функция расстояния от вершины ствола до искомого диаметра.
Так как кривая древесного ствола имеет два перегиба (в верхней и особенно в нижней части), она не укладывается в логарифмическую кривую и лишь в средней части напоминает ее.
Жаккард, Гуттенберг и другие исследователи утверждали, что живой организм — дерево нельзя приравнивать к простому брусу, находящемуся под влиянием сил только внешнего воздействия, что на формирование древесного ствола, помимо механических факторов, оказывают влияние анатомическое строение, физиологические процессы и т. д.
Однако симметричное строение древесного ствола на вертикальных и поперечных разрезах логически приводит к возможности приравнивания их формы к правильным стереометрическим фигурам – полным и усеченным телам вращения. Вершину древесного ствола можно рассматривать как конус; комлевую часть с корневыми наплывами — как усеченный нейлоид; наконец, большую часть средины ствола в виде усеченного параболоида, а на отдельных коротких секциях форма близка к цилиндру.
Иное направление имеют исследования Менделеева Д. И., Бе-лоновского И. Г., Хойера и других, которые поставили перед собой задачу установить вид «образующей» древесного ствола и выразить ее соответствующими математическими уравнениями, не исследуя факторы, под влиянием которых происходит формирование древесного ствола.
При этом они исходили из общей зависимости диаметра ствола Д и его высотой Н, выражаемой уравнением общего вида: Д = f(Н) ипредложили для «образующей» древесных стволов использовать наиболее простую форму этой функции в виде уравнений параболы. Так как образующая ствола имеет эсобразный характер, то лучшие результаты были получены при использовании уравнения третьей степени:
Y = А + Вх + Сх2 + Dx3,
где А, В, С, D — некоторые постоянные;
х — расстояние от шейки корня до рассматриваемого сечения;
В частности, Менделеев Д. И. использовал формулу для определения объемов древесных стволов при изучении лесосырьевой базы металлургических заводов Урала еще в 90 годах 19 века.
Вимменауэр К. (1918), учитывая влияние корневых наплывов и конусовидной вершины на форму образующей ствола, использовал уравнение четвертой степени: Y = А + Вх + Сх2 + Dx3 + Ex4,
Ряд авторов (Хойер, Гогенадль и др.) предложили выражать вид образующей древесного ствола при помощи уравнения логарифмической кривой.
 |
Для установления объема ствола на основе величины диаметра на высоте 1,3 м и высоты дерева в таксации введено понятие - видовое число f, которое представляет соотношение объема ствола с объемом одномерного цилиндра, имеющего со стволом одинаковую высоту Н и площадь сечения g, взятую на высоте 1,3 м.
Это соотношение получило название «старого видового числа» (от немецкого слова Formzahl) и определяется математически следующим соотношением: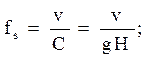 
. Откуда v = Cfs = gHf = 
где: v – объем ствола; С – объем одномерного цилиндра.
Из формулы видно, что объем ствола равен произведению объема цилиндра на видовое число. Таким образом, видовое число является переводным коэффициентом для перехода от объема цилиндра к объему ствола.
Таким же образом вычисляется видовое число для всего дерева, т.е. объема ствола с кроной fB = 
Разность между видовыми числами объема дерева fB и объема стволa fs составит видовое число объема сучьев fa, т.е. fa - fB = fs.
Видовые числа древесных стволов, характеризующие соотношения объемов ствола и одномерного цилиндра, дают представление о полнодревесности стволов. Например: при величине видового числа от 0,35 до 0,4 стволы характеризуются малой полнодревесностью; при видовом числе равном 0,5– средней полнодревесностью; и наиболее полнодревесные стволы имеют видовое число от 0,6 до0,7.
Для характеристики формы древесных стволов, отражающей их сбег Шиффель (1899) предложил взаимосвязи коэффициентов формы q2 с видовыми числами и высотами, выраженные эмпирическими формулами.
Например, взаимосвязь f и q2 . Объем ствола по простой формуле срединного сечения равен: V = g H.
Объем одномерного цилиндра C = g1,3 H,
где q1,3 — площадь сечения на высоте 1,3 м. Видовое число определяется следующим образом 
где d ½ - диаметр ствола на половине высоты. Это соотношение получило название формулы Вейзе.
Таким образом, видовое число f равно квадрату коэффициента формы g2.
Точность величины f определяемой по этому способу обусловливается точностью нахождения объема стволов по простой формуле срединного сечения и для отдельных стволов может давать отклонения до ±10% и больше. Если брать средние величины f для нескольких стволов, то может быть получена более высокая точность.
Изучая изменения видовых чисел по высотам и коэффициентам формы q2, Шиффель пришел к выводу, что изменения видовых чисел выражаются уравнением следующего вида: f = a + bq2 + 
,
где: f — видовое число ствола;
q2 — коэффициент формы – q2= 
;
Н – высота ствола;
а, b, с — некоторые постоянные коэффициенты.
А. Шиффелем были установлены цифровые параметры для вычисления видовых чисел лиственницы, сосны, пихты, ели. Однако в дальнейшем при использовании этой взаимосвязи для одинаковых q2, H и d1,3 влияние древесной породы на величину видового числа и объема древесных стволов оказалось практически незначительным. Для всех древесных пород объем ствола им рекомендовалось определять по формуле
V = g1,3H(0,14+0,66q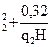 
).
Из формулы видно, что величина f является функцией двух переменных величин q2 и Н. При неизменности величины Н и повышении q2 видовое число увеличивается. Наоборот, при одинаковых q2 видовое число находится в обратной зависимости от Н, т.е. уменьшается.
Поэтому опираясь на последующие исследования этих соотношений М.Е. Ткаченко сформулировал закон формы древесных стволов.
Стволы хвойных и лиственных пород, взятые из древостоев, растущих при любых естественноисторических условиях, подчиняются одному и тому же закону формы стволов: при равных высотах, диаметрах и коэффициентах формы q2 стволы всех древесных пород имеют близко равные видовые числа, а следовательно, и близко равные объемы.
Основываясь на таких выводах, проф. М.Е. Ткаченко предложил таблицу всеобщих видовых чисел в зависимости от высот и коэффициентов формы q2.
Значения видовых чисел по классам коэффициента формы q2
| Высота, м | Значения видовых чисел по классам коэффициента формы, 0,001 | ||||
| 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | |
Из таблицы видно, что с увеличением видовых чисел повышаются значения q2 при данной высоте и, наоборот, при одинаковых q2 видовые числа уменьшаются по мере увеличения высот H.
Таким образом, основной недостаток предложений А. Шиффеля заключается в том, что коэффициенты формы хотя и дают общее представление о строении древесных стволов, но, находясь в зависимости от высоты стволов, искажают представление о действительной их форме.
Например, для Н=2,6 м, q2=1, а для стволов с высотой меньше 2,6 м q2 получается меньше единицы.
Из сделанного обзора методов изучения формы древесных стволов можно видеть, что эта проблема не получила еще окончательного разрешения и нуждается в дальнейших исследованиях таксаторов.
Чтобы исключить влияние высоты дерева и его диаметра на высоте 1,3 м на характер формы стволов, проф. В. К. Захаров предложил методические приемы, заключающиеся в следующем: древесный ствол делится на десять одинаковых по длине секций, равных 0,1 Н; измеряется диаметр ствола в коре и без коры, начиная от шейки корня на относительных высотах: 0—0,1—0,2—0,3—0,4—0,5—0,6—0,7—0,8—0,9—1,0, дополнительно измеряется диаметр на высоте 1,3 м. При последующих расчетах диаметры ствола на 0,1 Н принимаются за 100%, а диаметры на остальных относительных высотах выражаются в процентах от исходного диаметра на 0,1 Н.
Взятие в качестве опорной величины диаметра на 0,1 Н объясняется тем, что на уровне этой высоты практически не заметно влияние корневых наплывов, благодаря этому ствол приобретает более правильную форму.
Для получения среднего значения сбега стволов с точностью до одного процента необходимо измерить по этой методике для каждой ступени толщины 8—10 стволов, а всего для насаждения — до 150 стволов.
Как показали последующие исследования, средние проценты сбега на одинаковых относительных высотах в пределах одной породы оказались статистически достоверными и не зависящими от диаметра ствола на 1,3м и его высоты, а также условий среды и носят стабильный характер. Вычисляемые средние значения сбега по относительным высотам на основе 150 обмеров определяются с точностью в пределах одного процента.
Изложенным методом исследована средняя форма относительного сбега по относительным высотам семи древесных пород: березы, дуба, ясеня, сосны, ольхи, черной, осины, ели.
Результаты исследований позволили профессору В.К. Захарову выдвинуть гипотезу о единстве средней формы отдельных древесных пород, выраженной в относительных величинах, как по высотам, так и по диаметрам.
Влияние условий местопроизрастания (бонитета, типа леса) при одинаковом возрасте деревьев четко выражается в различной величине их средних диаметров, высотах и других таксационных признаков, однако при этом сохраняется стабильная форма стволов данной породы.
Зная величину диаметра на 0,1 Н и средние проценты сбега по относительным высотам для исследуемой породы, можно осуществить переход от относительных величин сбега к абсолютным. С этой целью абсолютную величину диаметра на 0,1 Н каждой ступени толщины последовательно умножают на средние коэффициенты сбега данной породы по относительным высотам. Этот прием позволяет восстановить параметры формы стволов необходимые для последующего определения его объема.
