Указания к выполнению индивидуальной работы 1
| Вариант | Номера задач | |||||||
Индивидуальная работа № 1
Дифференциальное исчисление функции одной переменной
1-10. Найти производные функции:
1. 
2. 
3. 
4. 
5. 
6. 
7. 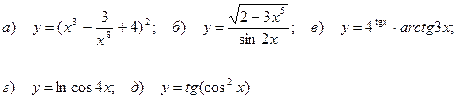
8. 
9. 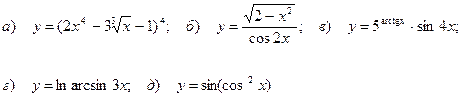
10. 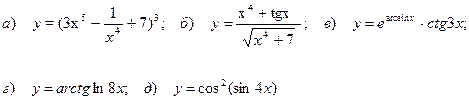
11-20. Найти производные второго порядка от функций:
11. а) у = cos3х · еsinх б) у = lnarctg 2x
12. а) у = 23х · tg2х б) у = cosln 5х
13. а) у = еtgх · ln2х б) у = cos 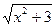
14. а) у = 28х · tg3х б) у = arcsin ln4х
15. а) у = еtgх · sin4х б) у = sin ln5х
16. а) у = 3ctgх · arcsin (х2) б) у = lnsin 6х
17. а) у = есtgх · cos6х б) у = sin ln2х
18. а) у = 4cosх · arctg2х б) у = lncos 5х
19. а) у = ех² · tg7х б) у = arcsin ln2х
20. а) у = 2sinх · arcsin2х б) у = lncos 7х
21-30. Найти пределы, раскрывая неопределенности по правилу Лопиталя.
21. 
22. 
23. 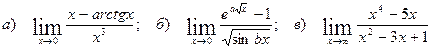
24. 
25. 
26. 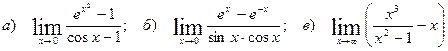
27. 
28. 
29. 
30. 
Применения дифференциального исчисления
31-40. Исследовать функции и построить их графики.
31. а) у = 2х3 + 3х2 – 36х – 21; 
в) у = 2sin2 2х +1, 0 £ x £ p/2
32. а) у = 2х3 + 15х2 + 36 + 32; 
в) у = –cos2 2х +2, p/4 £ x £ p/4
33. а) у = 2х3 – 15х2 + 24х + 4; 
в) у = – ln2 |х|
34. а) у = 2х3 – 9х2 – 24х + 61; 
в) у = e sinx – 2, 0 £ x £ p
35. 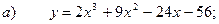

в) у = 2cosx, – p £ x £ p
36. 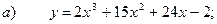

в) у = – arcsin|x| + p/2, –1£ x £ 1
37. 

в) у = – arccos|x| – p
38. 

в) у = – 2arctgx2
39. 

в) у = – 2xsinх, p/2 £ x £ p/2
40. 

в) у = 3–sinx, – p/2 £ x £ p
41-50. Найти наибольшее и наименьшее значения функции у = f(х) на отрезке [α; β] и написать уравнения касательной и нормали к кривой у = f(х) в точке х0:
41.  , х0=1
, х0=1
42.  , х0=–1
, х0=–1
43.  , х0=2
, х0=2
44.  , х0=–2
, х0=–2
45.  , х0=1
, х0=1
46. 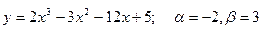 , х0=–1
, х0=–1
47.  , х0=3
, х0=3
48.  , х0=–3
, х0=–3
49.  , х0=1
, х0=1
50.  , х0=2
, х0=2
Неопределенный интеграл
51-60. Вычислить неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
51.  ;
;  ;
;  ;
;
 ;
; 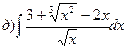 ;
; 
52.  ;
;  ;
;  ;
;  ;
;  ;
; 
53.  ;
;  ;
; 
 ;
;  ;
; 
54.  ;
;  ;
;  ;
; 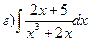 ;
;  ;
; 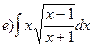
55.  ;
;  ;
;  ;
;  ;
;  ;
; 
56. 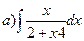 ;
;  ;
; 
 ;
;  ;
; 
57.  ;
;  ;
; 
 ;
;  ;
; 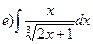
58. 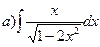 ;
;  ;
; 
 ;
; 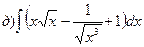 ;
; 
59.  ;
;  ;
; 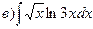
 ;
;  ;
; 
60. 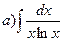 ;
;  ;
; 
 ;
;  ;
; 
Определенный интеграл
61-70. Вычислить определенные интегралы:
61. 

62. 
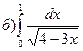
63. 

64. 

65. 

66. 

67. 

68. 

69. 

70. 
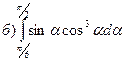
71-80. Вычислить площадь фигуры, ограниченной заданными кривыми:
71. a)  б)
б)  в)
в) 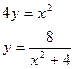
72. a)  б)
б)  в)
в) 
73. а)  б)
б)  в)
в) 
74. а)  б)
б)  в)
в) 
75. а)  б)
б)  в)
в) 
76. а)  б)
б)  в)
в) 
77. а)  б)
б)  в)
в) 
78. а) 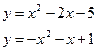 б)
б)  в)
в) 
79. а)  б)
б)  в)
в) 
80. а)  б)
б)  в)
в) 
Индивидуальная домашняя работа № 2
Указания к выполнению индивидуальной работы 2
| Вариант | Номера задач | ||||||
Функции нескольких переменных
1-10. Вычислить частные производные и полные дифференциалы от заданной функции
1. а)  б)
б) 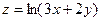
2. а)  б)
б) 
3. а)  б)
б) 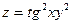
4. а)  б)
б) 
5. а)  б)
б) 
6. а)  б)
б) 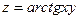
7. а)  б)
б) 
8. а)  б)
б) 
9. а) 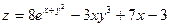 б)
б) 
10. а)  б)
б) 
11-20. Найти экстремумы функций двух переменных.
11. 
12. 
13. 
14. 
15. 
16. 
17. 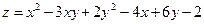
18. 
19. 
20. 
21-30. I. Найти двумя способами производную функции у = f(х), заданной в неявном виде уравнением F(x,y)=0 (1): а) путем дифференцирования по х обеих частей уравнения (1), б) пользуясь правилом дифференцирования сложной функции, по формуле 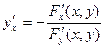 . II. Вычислить f/(x0), если f (x0)=y0.
. II. Вычислить f/(x0), если f (x0)=y0.
21. 
22. 
23. 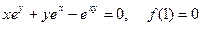
24. 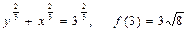
25. 
26. 
27. 
28. 
29. 
30. 
Обыкновенные дифференциальные уравнения
31-40. Найти, какая из функций y=f(x), y=j(x) является решением данного дифференциального уравнения;
31. 
32. 
33. 
34. 
35. 
36. 
37. 
38. 
39. 
40. 
41-50. Найти общее решение дифференциального уравнения первого порядка;
41. а)  б)
б) 
в)  г)
г) 
42. а)  б)
б) 
в)  г)
г) 
43. а) 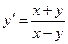 б)
б) 
в)  г)
г) 
44. а)  б)
б) 
в)  г)
г) 
45. а)  б)
б) 
в)  г)
г) 
46. а)  б)
б) 
в) 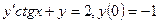 г)
г) 
47. а) 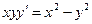 б)
б) 
в)  г)
г) 
48. а)  б)
б) 
в)  г)
г) 
49. а)  б)
б) 
в)  г)
г) 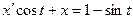
50. а)  б)
б) 
в)  г)
г) 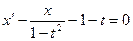
51-60. Найти частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям.
51. а) 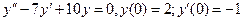 б)
б) 
52. а)  б)
б) 
53. а)  б)
б) 
54. а)  б)
б) 
55. а)  б)
б) 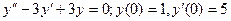
56. а)  б)
б) 
57. а)  б)
б) 
58. а)  б)
б) 
59. а)  б)
б) 
60. а)  б)
б) 
61-70. Найти общее решение неоднородного линейного уравнения второго порядка с постоянными коэффициентами.
61. 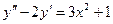
62. 
63. 
64. 
65. 
66. 
67. 
68. 
69. 
70. 






