Тема 5.1 Производная функции.
№1. Найти производную функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  д)
д)  ; е)
; е)  ;
;
ж) 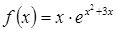 ; з)
; з)  .
.
№2. Напишите уравнение касательной к графику функции  в точке
в точке  .
.
№3. Составить уравнение касательной к кривой  ,которая проходит параллельно прямой
,которая проходит параллельно прямой 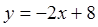 .
.
№4. Скорость точки, которая движется прямолинейно, задана уравнением  . В какой момент времени ускорение точки будет равно 2м/с2?
. В какой момент времени ускорение точки будет равно 2м/с2?
№5. Точка движется по координатной прямой по закону  . В какой момент времени скорость точки будет равна 19? (
. В какой момент времени скорость точки будет равна 19? ( - координата точки в момент времени
- координата точки в момент времени  ).
).
№6. Вращение тела вокруг оси происходит по закону  . Найти, в какой момент времени тело остановится (t- время в секундах,
. Найти, в какой момент времени тело остановится (t- время в секундах,  - угол поворота в радианах)
- угол поворота в радианах)
№7. По прямой движутся две материальные точки по законам  и
и  . В какой момент времени их скорости будут равны?
. В какой момент времени их скорости будут равны?
Тема 5.2. Исследование функций с помощью производной.
№1. Проведите полное исследование функции  по данной схеме и постройте его график.
по данной схеме и постройте его график.
Схема исследования функции для построения ее графика:
1.Найти область определения функции.
2.Выяснить, является ли функция четной и нечетной (или периодической)
3.Точки пересечения графика с осями координат (если их можно найти).
4.Производная и критические точки функции.
5.промежутки возрастания и убывания, точки экстремума и значения функции в этих точках.
6.Поведение функции на концах промежутков области определения и асимптоты графика функции (вертикальные, горизонтальные и наклонные).
7.Вторая производная и исследование функции на выпуклость и точки перегиба (и значения функции в этих точках)
8.Найти координаты дополнительных точек графика функции (если нужно уточнить его поведение).
9. На основании полученного исследования построить график функции.
№2. Разбейте число 18 на два положительных слагаемых так, чтобы сумма удвоенного первого слагаемого и квадрата второго слагаемого была наименьшей.
№3. Площадь прямоугольника равна 25 см2. Найдите наименьший возможный периметр этого прямоугольника.
№4. Периметр равнобедренного треугольника равен 60 см. При каком значении высоты, проведенной к основанию треугольника, площадь треугольника наибольшая?
№5. На странице текст занимает 384 см2. Верхнее и нижнее поля должны быть по 2 см, правое и левое – по 3 см. Какими должны быть размеры страницы с точки зрения экономии бумаги?
Тема 6.1 Неопределенный интеграл; решение задач.
№1. Найдите неопределенный интеграл:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; тд)
; тд) 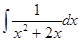 ; е)
; е)  ; ж)
; ж)  ;
;
з)  ; и)
; и)  ; к)
; к)  ; л)
; л)  ;
;
м) 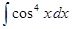 ; н)
; н) 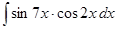 ; о)
; о) 
Тема 6.2. Определенный интеграл.
№1. Подготовить реферат на одну из тем:
1)Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла.
2)Интеграл и его применение.
3)Общее понятие определенного интеграла, его геометрический и механический смысл.
4)Применение определенного интеграла к решению физических задач.
5) Применение определенного интеграла к вычислению площадей плоских фигур.
6) Применение определенного интеграла к вычислению объемов.
7)Свойства определенного интеграла.
8)Методы интегрирования.
9)Интегральное исчисление. Исторический очерк.
10)Лейбниц Готфрид Вильгельм.
№2. Вычислить интеграл:
а)  ; б)
; б)  ;
;
№3. Дана функция  .
.
Вычислить: а)  ; б)
; б)  .
.
№4. Вычислите площадь фигуры, ограниченной линиями  и
и 
№5. Вычислите площадь фигуры, ограниченной графиком функции  , касательной к этой параболе в ее вершине и прямой
, касательной к этой параболе в ее вершине и прямой  .
.
№6. Найдите объем тела, полученного вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
а)  ,
,  ,
, 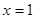 ,
,  ; б)
; б)  ,,
,, 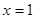 ,
,  ;
;
№7. Найдите объем тела, полученного вращением вокруг оси абсцисс фигуры, ограниченной линиями:
а)  ,
,  ; б)
; б) 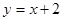 ,,
,,  ,
,  ,
,  ;
;
№8. Скорость движения точки меняется по закону  , где
, где  - скорость, м/с; t - время, с. Найдите:
- скорость, м/с; t - время, с. Найдите:
а) путь пройденный точкой за первые три секунды движения;
б) путь, пройденный точкой за третью секунду;
в) путь, пройденный точкой от начала движения t=0 до ее остановки.
№9. Вычислить работу, которую надо затратить, чтобы растянуть
пружину, находящуюся в положении равновесия, на 10 см. Известно, что при
растяжении пружины на 1 см сила натяжения равна 5 Н.
№10. Дан прямоугольный неоднородный стержень, плотность в точке  определяется по формуле
определяется по формуле  . Найдите массу
. Найдите массу  стержня длиной
стержня длиной  .
.






