Методика изучения основного уравнения МКТ ИГ

Выводу основного уравнения молекулярно-кинетической теории идеального газа должно предшествовать изучение таких понятий, как давление газа в МКТ и средний квадрат скорости теплового движения молекул. Изучение этих вопросов позволяет подготовить учащихся к восприятию вывода основного уравнения МКТ.

На данный момент существует несколько вариантов вывода основного уравнения МКТ, которые отличаются незначительными деталями при общем принципе, положенном в основу вывода: рассматривается изменение импульса стенки, с которой сталкиваются молекулы и вычисляют силу, с которой молекулы действуют на эту стенку.

v

v

v y

vy

vx

vx

A

B

C

D

Y

X

При выводе основного уравнения МКТ газов рассматривают абсолютно упругие соударения молекул идеального газа с некоторой массивной стенкой (на рисунке стенка СD). Прежде чем приступить к выводу основного уравнения МКТ, необходимо повторить те основные понятия, которые придется использовать при выводе. К таким понятиям в первую очередь относится понятие идеального газа. Важно подчеркнуть, что движение каждой молекулы подчиняется законам Ньютона и взаимодействие их между собой и со стенками сосуда происходит по закону абсолютно упругого удара. При повторении теплового движения молекул необходимо еще раз обратить внимание учащихся на хаотичность данного движения, что позволит считать все направления движения равноправными и принять равными средние значения квадратов проекций скоростей на координатные оси. Целесообразно повторить понятие среднего квадрата скорости. Кроме того, при выводе основного уравнения МКТ используют ряд понятий и законов механики, которые также необходимо актуализировать: импульс тела, импульс силы, давление, второй и третий законы Ньютона.

Некоторую методическую трудность создает тот факт, что давление и импульс обозначаются одной буквой р, поэтому приходится подробно записывать все рассуждения. Логика рассуждений должна быть ясна и понятна учащимся.

Согласно ранее изученному, давление газа на стенку обусловлено ударами молекул. При ударе молекул о стенку, они передают ей импульс. Импульс, полученный стенкой равен суммарному изменению импульса всех молекул, которые ударились об неё.

В первую очередь вспоминается известная учащимся формула для нахождения давления тела на опору .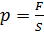

Затем из механики вспомиинается формула, связывающая импульс силы с изменением импульса тела.

,

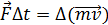Откуда можно сделать вывод, что сила равна изменению импульса стенки за единицу времени.

Каждая молекула массой m ₀, подлетающая к стенке со скоростью v, проекция которой на ось ох равна v_х, передает стенке при абсолютно упругом ударе импульс 2 m₀v_x.

Все молекулы, ударившиеся о стенку передадут ей суммарный импульс, равный

2 m₀v_xz, где z – число столкновений.

На основе качественных рассуждений, учащимся необходимо показать, что число столкновений z пропорционально концентрации молекул, их скорости, а также площади поверхности стенки.

Исходя из того, что движение молекул хаотично, поэтому все направления равновероятны и в каждый момент времени в среднем в противоположных направлениях движется одинаковое количество частиц, значит нужно учесть, что в каждый момент времени примерно половина молекул движется в сторону стенки, и половина в противоположную, то есть число ударов молекул о стенку за единицу времени равно

.

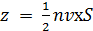Тогда полный импульс, переданный стенке за 1 с, равен:

2 m₀v_xz = m₀v²_xnS.

А значит сила, действующая на стенку со стороны молекул равна

F = m₀v²_xnS.

Учитывая, что

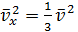, и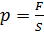

Окончательно выводится основное уравнение молекулярно-кинетической теории идеального газа

.

Если учесть понятие средней кинетической энергии молекул газа, то уравнение можно записать в виде

При анализе уравнения необходимо обратить внимание учащихся на то, что оно связывает макроскопический параметр состояния газа - давление с характеристиками отдельных молекул. Это уравнение имеет смысл только для совокупности молекул и носит статистический характер.

Основное уравнение молекулярно-кинетической теории идеального газа следует проиллюстрировать числовыми примерами.

Методика формирования термодинамических понятий

В термодинамике основным понятием является понятие «внутренняя энергия». Внутренняя энергия системы – это суммарная энергия всех составных частей системы и их взаимодействий. Это кинетическая энергия хаотического теплового движения частиц системы, потенциальная энергия их взаимодействия, обусловленная структурой системы, энергия электронов на атомных и молекулярных орбиталях, энергия связи в атомных ядрах, энергия элементарных частиц. Она не включает кинетической и потенциальной энергии системы как целого. Внутренняя энергия является однозначной функцией состояния тела, которое определяется рядом параметров (давление, объем, температура). Это означает, что в каждом состоянии тело (или система) облада­ет лишь одним значением внутренней энергии. Следовательно, изменение внутренней энергии системы при переходе из одного состояния в другое не зависит от этогопере­хода, т.e. внутренняя энергия является функцией состояния сис­темы, а не функцией процесса.

Если рассматривать идеальный газ, то его внутренняя энергия представляет собой только суммарную кинетическую энергию теплового движения его молекул. Именно такое понимание и должно быть сформировано у учащихся. В этом случае все-таки методически верно показать учащимся, откуда берется формула для расчета внутренней энергии. Термодинамическая трактовка понятия внутренней энергии не полностью раскрывает его смысл. Для более полного определения этого понятия необходимо рассмотреть его молекулярно-кинетическую трактовку.

Это можно сделать на основе следующих рассуждений.

Внутренняя энергия равна суммарной кинетической энергии молекул идеального газа

.

Где – 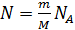число молекул в газе, а – средняя кинетическая энергия одной молекулы одноатомного газа. Тогда

. Учитывая, что 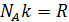окончательно

Последующий анализ этого уравнения позволяет сделать вывод о том, что внутренняя энергия идеального газа прямо пропорциональна абсолютной температуре и зависит только от температуры.

Переход к изучению понятий «работа» и «количество теплоты» связан с актуализацией знаний из курса физики основной школы о способах изменения внутренней энергии. В 8 классе был фактически на качественном уровне сформулирован первый закон термодинамики: внутреннюю энергию можно изменить либо теплопередачей, либо совершением работы.

Вначале необходимо записать формулу изменения внутренней энергии

Внутренняя энергия может изменяться под действием каких-либо внешних факторов: либо при совершении работы, либо в процессе теплопередачи. В первом случае мерой изменения внут­ренней энергии является работа, во втором - количество переданной теплоты. Работа, так же как и количество теплоты, зависит не только от конечного и начального состояний системы, но и от того, при каком процессе происходило изменение состояния. Количество теплоты и работа характеризуют процесс изменения состояния и не являются функциями состояния.

Следует разъяснить школьникам, что работа и теплопередача - неравноценные способы изменения энергии. Работа - изменение энергии упорядоченного движения, совершение работы может привести к изменению как механической, так и внутренней энер­гии. При теплопередаче изменяется энергия хаотического движения частиц системы, а это ведет лишь к изменению ее внутренней энергии.