Справочный материал
1. Дифференциальным уравнением называют уравнение, содержащее независимую переменную х, искомую функцию у и ее производные различных порядков 
.
Наивысший порядок производной, входящей в дифференциальное уравнение, называют его порядком.
– дифференциальное уравнение n-го порядка.
– дифференциальное уравнение первого порядка.
– диф. уравнение первого порядка, разрешенное относительно производной.
2. Решением дифференциального уравнения называют всякую функцию, которая обращает уравнение в тождество.
Общим решением дифференциального уравнения 1 порядка называют такую функцию 
, 
, которая является решением дифференциального уравнения при каждом фиксированном с.
Частным решением дифференциального уравнения 1 порядка называют функцию 
, полученную из общего решения при конкретном значении 
.
Общее решение дифференциального уравнения, записанное в неявном виде 
, называется общим интегралом, тогдауравнение 
– частный интеграл.
Задача отыскание частного решения дифференциального уравнения, удовлетворяющего заданному начальному условию 
, называется задачей Коши.
3. Дифференциальным уравнением с разделяющимися переменными называют уравнение вида
(1)
(1/)
Правило решения:
1) разделить переменные;
2) интегрируя уравнение почленно, найти общий интеграл дифференциального уравнения;
3) выяснить имеет ли уравнение (1) особые решения, не входящие в общий интеграл;
4) если требуется, найти частные решения.
4. Однородным дифференциальным уравнением 1 порядка называют уравнение вида
(2)
где 
– однородная функция нулевого порядка, т.е.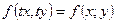 
, 
.
Однородное уравнение можно представить в дифференциальной форме:
, (2/)
где 
– однородные функции одного порядка.
При решении однородного уравнения его можно записать в виде: 
(2//)
и с помощью замены 
или 
, где 
– искомая функция, преобразовать в уравнение с разделяющимися переменными. Дифференцируя равенство , имеем 
. Подставляя у и 
в уравнение (2//), получим
– уравнение с разделяющимися переменными, решив которое и заменив u на 
, получим решение однородного уравнения (2//).
5. Линейное дифференциальное уравнение 1 порядка имеет вид:
(3)
Линейное уравнение содержит искомую функцию 
и ее производную 
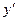и не содержит их произведений.
Линейное уравнение сводится к двум уравнениям с разрешающимися переменными при помощи подстановки 
, где , 
– функции от х, одну из которых можно выбрать произвольно. Тогда, дифференцируя подстановку, получаем 
Подставляя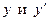 
в уравнение (3) и группируя относительно u, имеем
(3/)
Выбирая функцию v, так, чтобы выражение в скобках обращалось в нуль, получаем 
– уравнение с разделяющимися переменными, имеющее частное решение 
.
Подставляя 
в уравнение (3/), имеем 
– уравнение с разделяющимися переменными, откуда находим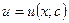 
. Тогда общее решение уравнения (3) имеет вид 
.
6. Уравнением Бернулли называют уравнение вида
(4)
Решают уравнение также как линейное, т.е. с помощью подстановки 
приводят к уравнению с разделяющимися переменными.
Задачи
1. Проверить, являются ли решениями (интегралами) дифференциальных уравнений данные функции
а) 
; б) 
;
в) 
; г) 
.
2. Найти общее (частное) решение дифференциального уравнения с разделяющимися переменными
а) 
; б) 
;
в) 
; г) 
;
д) 
; е) 
.
3. Найти общий интеграл однородного дифференциального уравнения
а) 
; б) 
;
в) 
; г) 
.
4. Найти общий (частный) интеграл линейного дифференциального уравнения
а) 
; б) 
;
в) 
; г) 
.
5. Решить уравнение Бернулли
а) 
; б) 
;
в) 
; г) 
.
6. Определить тип дифференциального уравнения и найти его общее (частное) решение
а) 
; б) 
;
в) 
; г) 
;
д) 
; е) ;
ж) 
; з) 
.
