Глава 3. Транспортная логистика

Транспорт является одним из важнейших звеньев материального потока. Транспортные расходы, при определенных условиях, могут достигать 20% цены продукции. Поэтому одним из важнейших аспектов транспортной логистики является сокращение затрат, связанных с перемещением товара.

Традиционно в литературе рассматривается ряд классических транспортных задач и методов их решения.

1. Транспортная задача. Основная цель данной задачи разработать матрицу перевозок от m поставщиков к n потребителям с наименьшими суммарными затратами на транспортировку.

2. Задача о назначениях. Имеется n работ и n претендентов на данные работы. Известна производительность претендентов на каждой работе. Необходимо распределить работы среди претендентов таким образом, чтобы суммарная производительность была максимальной. Решение данной задачи предполагает выполнение условий: количество работ должно равняться количеству работников; каждому работнику может быть назначена только одна работа и наоборот.

3. Задача о коммивояжере. Имеется n городов. Коммивояжер, выехав из первого города должен объехать все города по одному разу и вернуться в исходный пункт. Известны расстояния между городами. Цель данной задачи – определить кратчайший маршрут движения.

Помимо основных классических задач транспортная логистика также решает вопросы подбора транспортных средств, определения загрузки, количества и производительности транспорта и др.

Транспортная задача

В общем случае транспортная задача рассматривается как разработка наиболее экономичной структуры перевозки однотипной продукции из нескольких пунктов отправления в несколько пунктов назначения. Величина транспортных расходов задается с помощью тарифов на перевозку единицы груза. Транспортную задачу можно представить в виде сети с n пунктами отправления и m пунктами назначения.

 

a2

 

 

a_n n m

 

 

На приведенной иллюстрации используются следующие обозначения:

- а_1, …, а_n – объемы предложений;

- b₁, …, b_m – объемы спроса;

- с_i,j – стоимость перевозки единицы груза из пункта i в пункт j;

- х_i,j – объем перевозки единицы груза из пункта i в пункт j.

Цель задачи – найти план перевозок Х =(х_i,j), минимизирующий суммарные затраты. Приведем математическую модель транспортной задачи:

при ограничениях

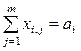, i = 1, …, n,

, j = 1, …, m,

х_{i , j} ³ 0, i = 1, …, n; j = 1, …, m.

 

Для решения транспортной задачи исходные данные удобно представлять в виде матрицы планирования.

 

Пункты предложения	Пункты назначения	Предложение (ед. продукции)
		...	m
	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	a1
	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	a2
…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	an
Спрос (ед.продукции)	b1	b2	…	bm

 

В соответствии с приведенной математической моделью, имеет место равенство суммарных предложения и спроса:

.

Очевидно, в реальности такая ситуация встречается далеко не всегда. Однако для решения любой транспортной задачи следует добиться этого равенства (искусственно, специальным образом). Если данное равенство выполняется, то такая задача называется сбалансированной (закрытой), в противном случае – несбалансированной (открытой). В том случае, если исходная транспортная задача не является сбалансированной, ее следует сбалансировать, то есть привести к закрытой форме. Для этого необходимо ввести фиктивные пункты назначения или предложения.

В ситуации, когда суммарное предложение превышает суммарный спрос, необходимо ввести фиктивный (реально не существующий) пункт назначения, который будет формально потреблять излишнее предложение:

 

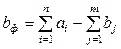
Пункты предложения	Пункты назначения	Предложение ед. продукции
		...	m	Фиктивный
	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	сф xф1,m	a1
	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	сф xф2,m	a2
…	…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	сф xфn,m	an
Спрос ед.продукции	b1	b2	…	bm	bф

 

Стоимость доставки единицы груза из любого пункта предложения в фиктивный пункт назначения принимают равной 0: сф = 0.

Если суммарный спрос превышает суммарное предложение, то вводят фиктивный пункт предложения, который формально восполняет недостаток предложения:

 

Пункты предложения	Пункты назначения	Предложение ед. продукции
		...	m
	с1,1 х1,1	с1,2 х1,2	…	с1,m x1,m	a1
	c2,1 x2,1	c2,2 x2,2	…	c2,m x2,m	a2
…	…	…	…	…	…
n	cn,1 xn,1	cn,2 xn,2	…	cn,m xn,m	an
Фиктивный	сф хфn,1	сф хфn,2		сф хфn,m	аф
Спрос ед.продукции	b1	b2	…	bm

 

Стоимость доставки единицы груза из фиктивного пункта предложения в любой пункт назначения принимают равной 0: сф = 0.

Решение транспортных задач проводится в два этапа: первоначальный и основной. На первоначальном этапе получают допустимое базисное решение, которое также называют опорным планом перевозок. Допустимое базисное решение удовлетворяет всем условиям задачи, кроме, быть может, оптимальности. Опорный план перевозок предполагает выполнение не более чем m + n – 1 поставок (заметим, что m + n – 1 – число линейно независимых ограничений системы ограничений). Можно показать, что всегда найдется такое оптимальное решение транспортной задачи, в котором количество поставок (занятых клеток в матрице планирования) также не превосходит числа m + n – 1. Поэтому оптимальный план перевозок ищут среди опорных планов.

Для нахождения первоначального решения используют методы северо-западного угла, наименьшей стоимости, Фогеля и др. Все эти методы предполагают решение одной задачи – построение начального опорного плана. Однако качество начального решения зависит от того, какой метод был использован для его получения. Как правило, метод северо-западного угла (очень простой в применении) дает решение, более далекое от оптимального плана поставок, по сравнению с методами наименьшей стоимости и Фогеля.

На основном этапе проводится последовательное улучшение начального опорного плана перевозок. В результате получается оптимальное базисное решение (оптимальный план перевозок), которое и является окончательным результатом для поставленной транспортной задачи. На основном этапе применяются распределительный метод, метод потенциалов и др.