Лекция 4.
Модели, построенные по временным данным, представляют модели временных рядов. Временной ряд – ряд значений какого-либо показателя, характеризующий один и тот же объект за несколько последовательных моментов или периодов времени. Уровень временного ряда складывается из следующих основных компонентов:
· трендовой компоненты, характеризующей основную тенденцию ряда (Т);
· циклической компоненты, характеризующей циклические колебания изучаемого явления (S);
· случайной компоненты, которая является результатом воздействия множества случайных факторов (Е).
При различных сочетаниях этих факторов зависимость уровней ряда от времени может принимать разные формы.
Во-первых, большинство временных экономических показателей имеют тенденцию, которая характеризует совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. По всей видимости, эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию (рис. 4.1).
yt
t
Рис. 4.1 Возрастающая тенденция временного ряда
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой бизнес-цикла, в которой находится страна.
уt
 |  |  | |||
t
Рис. 4.2. Сезонная компонента временного ряда
Некоторые временные ряды не содержат тенденции и циклическую компоненту, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательный) случайной компоненты.
уt
 | |||||
| |||||
 | |||||
t
Рис. 4.3. Случайная компонента временного ряда
Очевидно, что реальные данные не соответствуют полностью ни одной из описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных и случайной компоненты.
Фактический уровень временного ряда можно представить как функцию от этих компонент: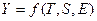 
. В зависимости от вида связи между этими компонентами может быть построена либо аддитивная модель: 
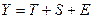, либо мультипликативная модель: 
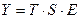ряда динамики.
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент, с тем чтобы использовать полученную информацию для прогнозирования будущих значений ряда или построении моделей взаимосвязи двух или более временных рядов.
При наличии тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих значений. Автокорреляция уровней ряда – корреляционная связь между последовательными уровнями одного и того же ряда динамики. Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов.
Пример. Пустьимеются следующие условные данные предприятия о средних расходах на конечное потребление за 8 лет (табл. 4.1).
Таблица 4.1
| Год, t | ||||||||
| Расходы на потребление, yt |
Можно предположить, что расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет.
Определим коэффициент корреляции между рядами уt и уt-1.
Одна из рабочих формул для расчета коэффициента корреляции имеет вид:
.
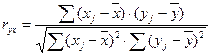В качестве переменной х рассмотрим ряд у2, у3,…,у8; в качестве переменной у – у1, у2,…,у7. Тогда приведенная выше формула примет вид:
,
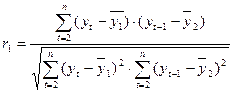где
; 
.
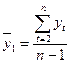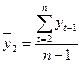Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда у t и у t-1, т.е. при лаге 1.
Таблица 4.2
Расчетные данные
| t | yt | yt-1 |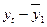 
| 
| ()*()
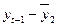
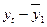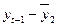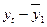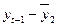| ()2
| ()2
|
| - | - -3,29 -3,29 -1,29 -0,29 0,71 2,71 4,71 | - -3 -2 -2 | - 9,87 6,58 2.58 0,71 5,42 18,84 | - 10,8241 10,8241 1,6641 0,0841 0,5041 7,3441 22,1841 | - | ||
| Итого | 53,4287 |
Для данного примера средние значения составят:
= 
;
.
.
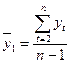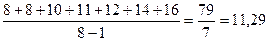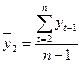
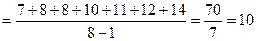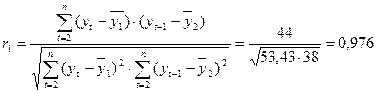Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующих годов и, следовательно, о наличие во временном ряде расходов на конечное потребление сильной линейной тенденции.
Аналогично можно определить коэффициенты второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями ряда у t и у t-2, и определяется по формуле:
,
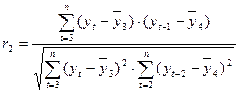где
; 
.
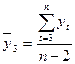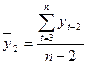Число периодов, по которым рассчитываются коэффициент автокорреляции, называется лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается.
Свойства коэффициента автокорреляции:
- так как он строится по аналогии с линейным коэффициентом корреляции, то он характеризует тесноту только линейной связи текущего и предыдущего уровней связи; по данному коэффициенту можно судить о наличии линейной тенденции; для некоторых временных рядов, имеющих сильную нелинейную тенденцию коэффициент может приближаться к нулю;
- по знаку коэффициента автокорреляции сделать вывод о тенденции ряда невозможно.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага называется коррелограммой.
Рассчитав несколько коэффициентов автокорреляции можно определить лаг, при котором автокорреляция наиболее высока, выявив тем самым структуру временного ряда. Если наиболее высоким оказывается значение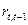 
, то исследуемый ряд содержит тенденцию; если наиболее высоким оказался 
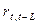, то ряд содержит циклические колебания с периодом L. Если ни один из коэффициентом не является значимым, можно сделать одно из двух предположений:
- либо ряд не содержит тенденции и циклических колебаний, а его уровень определяется только случайной компонентой;
- либо ряд содержит сильную нелинейную тенденцию.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
· линейная 
;
· гипербола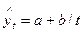 
;
· экспонента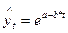 
;
· степенная функция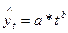 
;
· парабола второго и более высоких порядков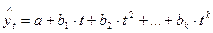 
.
Параметры трендов определяются МНК, в качестве независимой переменной выступает время, а в качестве зависимой переменной – фактические уровни временного ряда. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации.
Пример. Определим МНК параметры линейного тренда на основе данных табл. 4.3.
Таблица 4.3
