Основы дисперсионного анализа

В настоящее время дисперсионный анализ определяется как статистический метод, предназначенный для оценки влияния раз­личных факторов на результат эксперимента, а также для после­дующего планирования аналогичных экспериментов.

Первоначально (1918 г.) дисперсионный анализ был разра­ботан английским математиком-статистиком Р.А. Фишером для обработки результатов агрономических опытов по выявле­нию условий получения максимального урожая различных сор­тов сельскохозяйственных культур. Сам термин «дисперсионный анализ» Фишер употребил позднее.

По числу факторов, влияние которых исследуется, различа­ют однофакторный и многофакторный дисперсионный анализ.

В дисперсионном анализе общая вариация изучаемого признака подразделяется на составляющие и проводится сравнение этих составляющих. Проверяемая гипотеза заключается в том, что если данные каждой группы представляют случайную выборку из нормально распределенной генеральной совокупности, то величины всех частных дисперсий должны быть пропорциональны своим степеням свободы и каждую из них можно рассматривать как оценку генеральной совокупности.

В случае выделения групп по одному фактору мы имеем так называемый однофакторный дисперсионный комплекс. Разложение дисперсии при этом проводится в соответствии с правилом сложения дисперсии:

 

,

 

где 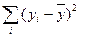- общая сумма квадратов отклонений,

- сумма квадратов отклонений, обусловленная регрессией

(факторная);

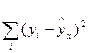- остаточная сумма квадратов отклонений.

На основе разложения дисперсии в соответствии с гипотезой отсутствия различий между группами могут быть получены три оценки генеральной дисперсии, пропорциональные степени свободы: на основе общей вариации, межгрупповой (факторной) и внутригрупповой (остаточной).

Число степеней свободы равно:

· для общей вариации df_общ = n – 1;

· для межгрупповой (факторной) вариации df_факт = m – 1;

· для внутригрупповой (остаточной) вариации df_ост = n – m.

Как и суммы квадратов отклонений, числа степеней свободы связаны между собой равенством: df_общ = df_факт + df_ост или n – 1=(m – 1)+(n – m).

Деление суммы квадратов отклонений на соответствующее число степеней свободы дает три оценки генеральной дисперсии:

 

, , .

 

 

Поскольку измеряет вариацию результативного признака, связанную с изменением фактора, по которому проведена группировка, а 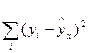– вариацию, связанную с изменением всех прочих факторов, сравнение этих величин, рассчитанных на одну степень свободы, дает возможность оценить существенность влияния признака-фактора на результативный признак с помощью F -критерия:

 

.

Данная запись предполагает, что ≥

Полученное значение F -критерия сравнивается с табличным значением F_табл -критерия. Если F_табл‹ F_факт, то гипотеза Н₀ о равенстве выборочных дисперсий генеральной дисперсии отклоняется, признается существенным, статистически значимым влияние признака-фактора на результативный признак.

F_табл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы () и уровне значимости , который принимается равным 0,05 или 0,01.

Если же величина F окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня, и она не может быть отклонена без риска сделать неправильный вывод о наличии связи.

Этапы однофакторного дисперсионного анализа представлены в таблице.

Источник вариации	Сумма квадратов отклонений	Число степеней свободы	Дисперсия на одну степень свободы (средний квадрат отклонений)	F -критерий
Общая		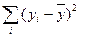n – 1		-
Факторная (между группами)		m – 1
Остаточная (внутри групп)		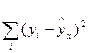n – m		-

 

Коэффициент корреляции

 

Перейдем к оценке тесноты корреляционной за­висимости. Рассмотрим наиболее важный для практики и тео­рии случай линейной зависимости.

На первый взгляд подходящим измерителем тесноты связи у от х является коэффициент регрессии b_ух, так как он показывает, на сколько единиц в среднем изменяется у, когда х увеличивается на одну единицу. Однако b_yx зависит от единиц измерения переменных.

Очевидно, что для «исправления» b_ух как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Статистика знает такую систему еди­ниц. Эта система использует в качестве единицы измерения пе­ременной ее среднее квадратическое отклонение .

Введем формулу:

 

.

 

В ней r_yx показывает, на сколько величин 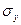изменится в среднем y, когда x увеличится на одно значение .

Величина r является показателем тесноты линейной связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).

На рисунке 1.1 приведены две корреляционные зависимости переменной у от х. Очевидно, что в случае а) зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б), так как точки корреляционного поля а) дальше отстоят от линии регрессии, чем точки поля б).

Рис. 1.1 Корреляционные зависимости

 

Нетрудно видеть, что r совпадает по знаку с b_ух (а значит, и с b_ху).

Если r > 0 (b_ух >0, b_ху >0), то корреляционная связь между переменными называется прямой, если r < 0 (b_ух <0, b_ху <0) — об­ратной. При прямой (обратной) связи увеличение одной из пе­ременных ведет к увеличению (уменьшению) условной (группо­вой) средней другой.

Формулу для r можно представить в виде:

r = ,

т.е. формула для r симметрична относительно двух переменных, и переменные у и х можно менять местами. Тогда аналогично формуле: можно записать: . Найдя произведение обеих частей равенств получим: r²= = b_ухb_ху или r= , т.е. коэффициент корреляции r переменных у и х есть средняя геометрическая коэффициентов регрессии, имеющая их знак.

Основные свойства коэффициента корреляции (при достаточно большом объеме выборки n):

1. Коэффициент корреляции принимает значения на отрезке
[-1,1], т.е.

-1 ≤ r ≤ 1.

В зависимости от того, насколько | r | приближается к 1, раз­личают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную, т.е. чем ближе | r | к 1, тем теснее связь.

2. Если все значения переменных увеличить (уменьшить) на од­но и то же число или в одно и то же число раз, то величина ко­эффициента корреляции не изменится.

3. При r корреляционная связь представляет линейную функ­циональную зависимость. При этом линии регрессии у пo х и х пo у совпа­дают и все наблюдаемые значения располагаются на обшей прямой (рис. 1.2.).

 

Рис.1.2 График линейной функциональной зависимости

4. При r = 0 линейная корреляционная связь отсутству­ет. При этом групповые средние переменных совпадают с их об­щими средними, а линии регрессии у пo х и х пo у параллельны осям координат.

Если r = 0, то коэффициент b_ух=b_ху =0, и линии регрессии имеют вид: у_х= и х_у= (рис. 1.3).

 

 

	Рис. 1.3 Линии регрессии

 

 

Равенство r = 0 говорит лишь об отсутствии линейной корреля­ционной зависимости (некоррелирован­ности переменных), но не вообще об отсутствии корреляционной, а тем более статистической, зависимости.

Пример. При исследовании корреляционной зависи­мости между объемом валовой продукции у (млн. руб.) и сред­несуточной численностью работающих х (тыс. чел.) для ряда предприятий отрасли получено следующее уравнение регрессии х по у: х_у=0,2у – 2,5. Коэффициент корреляции между этими признаками оказался равным 0,8, а средний объем валовой про­дукции предприятий составил 40 млн. руб.

Найти:

а) среднее значение среднесуточной численности работающих на предпри­ятиях;

б) уравнение регрессии у по х;

в) средний объем валовой продукции на предприятиях со среднесуточной численностью работающих 4 тыс. чел.

Решение: а) Обе линии регрессии у по х и х по у пере­секаются в точке (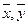), поэтому найдем по заданному уравнению регрессии при у = = 40,

т.е. = = 5,5 (тыс. чел.).

б) Учитывая, что: r²= = b_ухb_ху, вычислим коэффициент регрессии b_ух: b_ух= .

По формуле получим уравнение регрессии у по х: или .

в) у_х=4 найдем по полученному уравнению регрессии у по х: (млн. руб.).

Пример. Найти коэффициент корреляции между производительностью труда у (тыс. руб.) и энерговооруженно­стью труда х (кВт) (в расчете на одного работающего) для 14 предприятий региона по следующим данным:

х	2,8	2,2	3,0	3,5	3,2	3,7	4,0	4,8	6,0	5,4	5,2	5,4	6,0	9,0
у	6,7	6,9	7,2	7,3	8,4	8,8	9,1	9,8	10,6	10,7	11,1	11,8	12,1	12,4

Решение. Вычислим необходимые суммы:

 

Используя еще один вариант формулы для расчета r, получим:

Значение r=0,898 говорит о тесной связи между переменными.