ДЕФОРМАЦИЯ УДЛИНЕНИЯ-СЖАТИЯ.
Относительное удлинение 
Размерность – безразмерная величина
ЗАКОН ГУКА ДЛЯ ДЕФОРМАЦИИ УДЛИНЕНИЕ-СЖАТИЕ
Е – модуль Юнга, характеризующий упругие свойства вещества
Размерность 
(Паскаль)
ДЕФОРМАЦИЯ СДВИГА
γ - угол сдвига
tg γ – относительный сдвиг
Так как углы сдвига малы, можно считать, что
tg γ ≈ γ
Тогда ЗАКОН ГУКА ДЛЯ ДЕФОРМАЦИИ СДВИГА запишется следующим образом
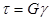,где G - модуль сдвига.
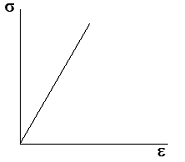
ДИАГРАММА РАСТЯЖЕНИЯ Диаграммой растяжения принято называть графическую зависимость σ от ε. Пример диаграммы растяжения для металлического образца изображен на рисунке. На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, согласно которому нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σП, при котором еще выполняется закон Гука, называют пределом пропорциональности. При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение σy нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной. Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Материалы, у которых область текучести 3-4 значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называются хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун. Нормальное напряжение σТ, при котором остаточная деформация достигает заданного значения, называют пределом текучести. При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика). Максимальное значение нормального напряжения σпр, при превышении которого происходит разрыв образца, называют пределом прочности.
Биологические ткани содержат в своем составе биополимеры – вещества, молекулы которых представляют собой длинные цепи. Это прежде всего белки (альбумин, коллаген, эластин), полисахариды, гликопротеиды и т.д. Их механические свойства резко отличаются от свойств низкомолекулярных веществ. Твердые тела(например, металлы) имеют малые и обратимые деформации при большом пределе прочности, так как силы упругости определяется изменениями межатомных расстояний. Жидкости обладают неограниченной деформацией при малой прочности. Полимеры достаточно прочны и вместе с тем способны к большим обратимым деформациям. При приложении постоянной нагрузки к полимеру его молекулы выпрямляются в соответствующем направлении, и длина образца увеличивается. Но это более длительный процесс, чем удлинение твердого тела при постоянной нагрузке. Свойство изменения деформации со временем при постоянной нагрузке называется ползучестью. Эти процессы в полимерах сходны с течением вязкой жидкости, поэтому процесс деформации их называют вязкоупругим.
Реологические модели
Упругие и вязкие свойства материалов (в том числе и биологических тканей) можно моделировать сочетанием идеально упругих и вязких элементов.
1) Идеально упругий элемент – пружина. Процесс деформации происходит мгновенно и подчиняется закону Гука.
В момент t1 удлиняем пружину на величину Δl. В момент t2 отпускаем пружину, и она возвращается в исходное состояние.
2) Идеально вязкий элемент
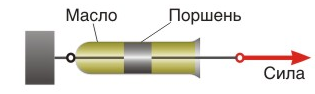
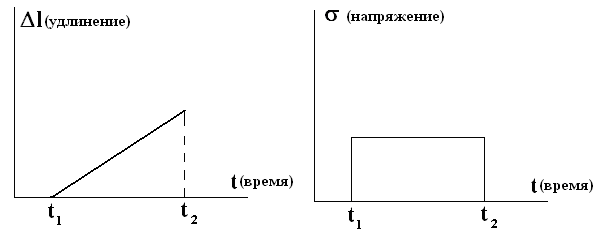
Поршень имеет отверстия, через которые вязкая жидкость может перетекать. В момент t1 под действием приложенной силы поршень перемещается, в момент t2 действие силы прекращается, но модель не возвращается в исходное состояние.
Теперь рассмотрим некоторые механические модели, описывающие вязкоупругие свойства различных тканей. Механические характеристики таких систем изучают либо в изотоническом режиме, создавая определенное напряжение под действием постоянной силы, и измеряя изменение со временем длины образца исследуемого материала. Изометрический режим предполагает ступенчатое изменение длины образца и измерение в новом состоянии изменения напряжения со временем.
Модель Максвелла
Изотонический режим
При быстром возникновении напряжения под действием постоянной силы происходит практически мгновенное удлинение пружины и медленное перемещение поршня
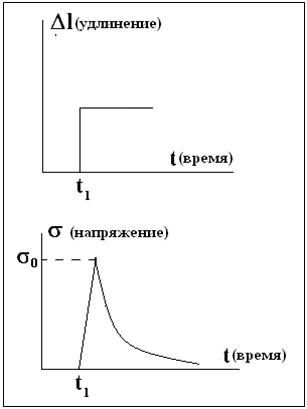
Изометрический режим
При изменении длины на определенную величину в системе возникает максимальное для заданной длины напряжение σ0 постепенно уменьшается по мере перемещения поршня (релаксация напряжения)
Гладкие мышцы и другие компоненты стенок полых органов (желчного и мочевого пузырей, желудка, кишечника, кровеносных (венозных) и лимфатических сосудов и т.д.) испытывают обычно длительное воздействие постепенно нарастающих растягивающих усилий и ведут себя наподобие тела Максвелла. Только в самом начале действия силы они напрягаются, проявляя свои слабые упругие свойства, но затем напряжение их постепенно ослабевает благодаря деформации компонентов, обладающих вязкостными свойствами. Поэтому полые органы способны сильно растягиваться без развития напряжения.
4) Модель Кельвина – Фойгта.
Изотонический режим.
При действии постоянной силы (т.е. создания постоянного напряжения) удлинение модели соответствует экспоненциальному закону. При снятии напряжения удлинение уменьшается по этому же закону, хотя могут присутствовать остаточные деформации.
Изометрический режим
Если удлинить модель на определенную величину, возникнет соответствующее напряжение, не меняющееся со временем.
МЕХАНИЧЕСКИЕ СВОЙСТВА КОСТНОЙ ТКАНИ.
Костная ткань – это композиционный материал, состоящий примерно на две трети из кристаллов минерала – гидроксилапатита и на одну треть – из коллагеновых волокон. При этом кристаллы гидроксилапатита расположены между коллагеновыми волокнами (фибриллами), что придает кости необходимые механические свойства – упругость и прочность. При небольших деформациях для костной ткани справедлив закон Гука, модуль Юнга может достигать 1010 Па, а предел прочности 108 Па.
Поведение костной ткани хорошо описывается механической моделью вида
