Целевая функция:
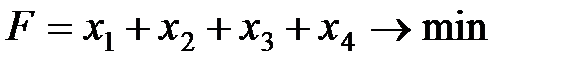(3)
Система ограничений задачи имеет вид:
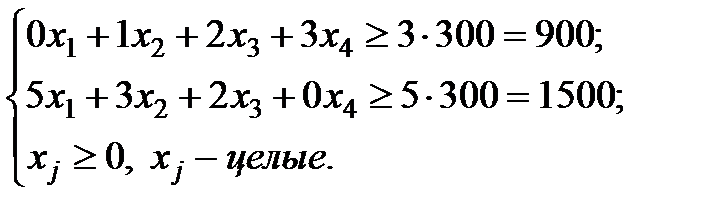(4)
Решение. Решим задачу линейного программирования (3), (4) с помощью возможностей табличного процессора MS Excel.
1. Запускаем MS Excel.
2. На листе в ячейки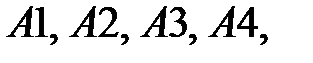 
зарезервированные для управляемых переменных 
, 
, 
, 
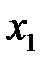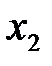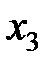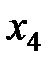соответственно, введём любые начальные значения. Пусть это будет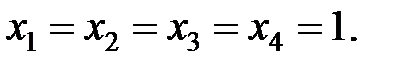 
3. В ячейку В1 введём формулу =0*А1+1*А2+2*А3+3*А4.
4. В ячейку В2 – формулу =5*А1+3*А2+2*А3+0*А4.
5. В ячейку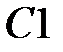 
– формулу =А1+А2+А3+А4.
6. Запускаем надстройку Поиск решения (Сервис 
Поиск решения).
7. В появившемся диалоговом окне введём информацию:
- Установить целевую ячейку: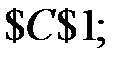 
- Равной: минимальному значению;
- Изменяя ячейки: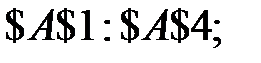 
- Ограничения: $B$1>=900; $B$2>=1500; $A$1:$A$4>=0; $A$1:$A$4 – целые.
8. Нажимаем кнопку Выполнить. В результате получаем следующее:
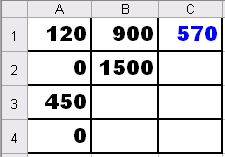
Интерпретация полученного результата. Оптимальное значение целевой функции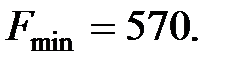 
Это значит, что нужно разрезать, как минимум, 570 заготовок, чтобы получить 300 комплектов столбов.
Переменные при оптимальном плане разрезания принимают значения: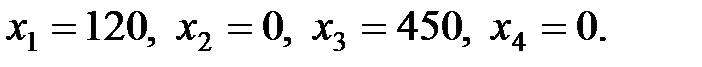 
Это означает, что по 1-му варианту нужно разрезать 120 заготовок, по 3-му – 450 заготовок, 2-й и 4-й варианты не используются как экономически невыгодные.
Задача 3. В исправительной колонии решили построить деревянную часовню из круглых брёвен. Имеются брёвна из дорогостоящей древесины длиной 10 метров. Для строительства нужны брёвна длиной 2,5 м, 3,5 м и 4,5 м в количестве 30, 40 и 60 штук соответственно.
Требуется найти такие сочетания различных вариантов разрезания стандартных брёвен, чтобы полностью удовлетворить потребность строительства с минимальными потерями (отходами).
Построение математической модели. Рассмотрим все возможные варианты распила стандартного бревна длиной 10 м, соответствующие данные приведем в таблице.
| Длина бревна (м) | Варианты разрезания | Минимальное количество брёвен | |||||
| 2,5 | |||||||
| 3,5 | |||||||
| 4,5 | |||||||
| Отходы (м) | 1,5 | 0,5 | 0,5 |
Определим переменные:
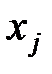– количество брёвен, разрезаемых по варианту 
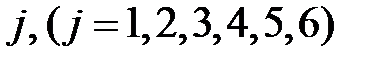. Ограничения непосредственно связаны с требованием обеспечить изготовление требуемого количества нестандартных бревен. Используя данные таблицы, получим:
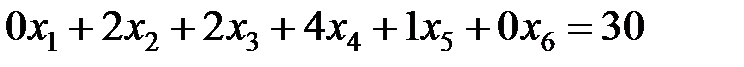– число столбов длиной 2,5 м;
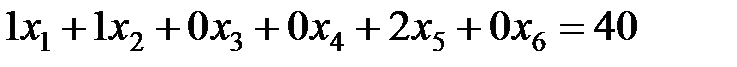– число столбов длиной 3,5 м;
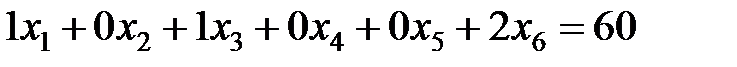– число столбов длиной 3,5 м.
Выражение для суммарной величины отходов (обрезки) имеет вид:
.
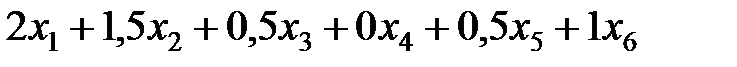Таким образом, математическая модель рассматриваемой задачи в общем виде выглядит следующим образом:
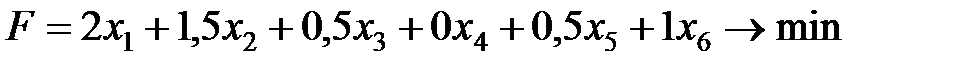(1)
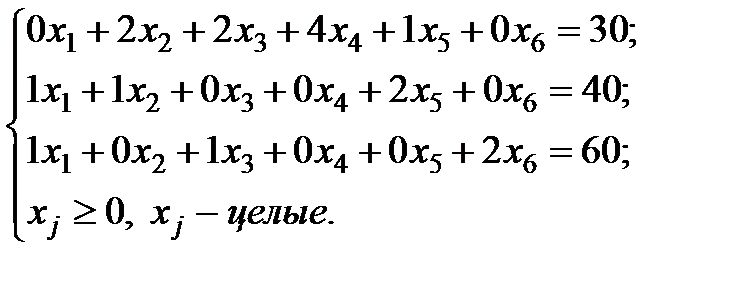(2)
Решение. Решим задачу линейного программирования (1), (2) с помощью возможностей табличного процессора MS Excel.
1. Запускаем MS Excel.
2. На листе в ячейки А1:А6, зарезервированные для управляемых переменных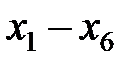 
соответственно, введём любые начальные значения. Пусть во всех ячейках будет 1.
3. В ячейку В1 введём формулу
=0*А1+2*А2+2*А3+4*А4+1*А5+0*А6.
4. В ячейку В2 – формулу =1*А1+1*А2+0*А3+0*А4+2*А5+0*А6.
5. В ячейку В3 – формулу =1*А1+0*А2+1*А3+0*А4+0*А5+2*А6.
6. В ячейку 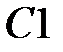– формулу =2*А1+1,5*А2+0,5*А3+0*А4+0,5*А5+1*А6.
7. Запускаем надстройку Поиск решения (Сервис Поиск решения).
8. В появившемся диалоговом окне введём информацию:
- Установить целевую ячейку: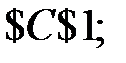 
- Равной: минимальному значению;
- Изменяя ячейки: $A$1:$A$6;
- Ограничения: $B$1=30; $B$2=40; $B$3=60; $A$1:$A$6>=0; $A$1:$A$6 – целые.
9. Нажимаем кнопку Выполнить. В результате получаем следующее:
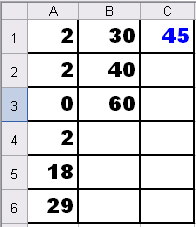
Интерпретация полученного результата. Оптимальное значение целевой функции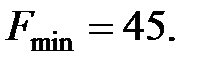 
Переменные при оптимальном плане разрезания принимают значения: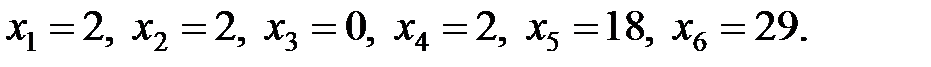 
Это означает, что по 1-му, 2-му и 4-му вариантам нужно распилить по 2 бревна, по 5-му – 18 брёвен, по 6-му – 29 брёвен, 3-й вариант не используется как экономически невыгодный. При таком плане разрезания брёвен количество отходов (суммарная длина обрезков) будет минимальным и составит 45 м.
ПРАКТИЧЕСКАЯ РАБОТА 16.5
