Практикум 1. Интегрирование
| Неопределённый интеграл. Определённый интеграл. |
| Символическое и численное интегрирование. |
Здравствуйте, меня зовут Жакрова Надежда Владимировна. Я у вас буду вести мат.ан и МАТЛАБ.
Свои комментарии к заданию я буду выделять «Ж:».
Мы также сможем общаться с вами через форму сайта www.numlock.ru.
Мой ник: abshope.
Также я буду вести электронный журнал учета успеваемости в документах Google/https://docs.google.com/.
Позже на www.numlock.ru. я выложу ссылки к вашим журналам.
Ж: Оригинал Практикума 1(оно расчитано на 2 занятия) выложен без изменений. Я предлагаю адаптированную версию этого задания.
Итак, за сегодняшнее занятие необходимо сделать пункты 1 и 2.
На второй странице дано ДЗ1 на ЧЕТВЕРГ. (для групп МП-11,17)
1. Символьное вычисление неопределённого интеграла. Неопределённые интегралы от символических функций вычисляются с помощью int, входными аргументами указываются символическая функция и переменная, по которой ведётся интегрирование.
Пример 1.
>> syms x; f=sym('x^3*exp(x)'); I=int(f,x)
I =
x^3*exp(x)-3*x^2*exp(x)+6*x*exp(x)-6*exp(x)
>> pretty(I)
Упражнение 1. Вычислить неопределённые интегралы:
а)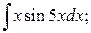 
б) 
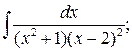в)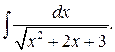 
Последний интеграл вычислить без использования MatLab, вывести формулу для функции, обратной гиперболическому синусу.
Ж: Замечание к Упражнению 1
Разумеется, все интегралы нужно посчитать вручную в тетради и показать. Затем сравнить результаты с теми, что выдает MatLab.
Для задачи под пунктом б) попробуйте взять аналогичные, но более простые примеры: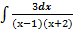 
= 
, 
,
.
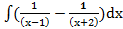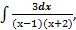
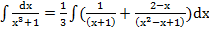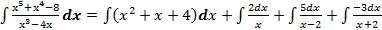При вычислении интеграла б) вручную, нужно будет подынтегральную функцию разложить на множители. Для определения коэффициентов разложения можно составить систему и решить ее по формулам Крамера. Попробуйте также с помощью функции int(f,x) найти этот интеграл, подставляя вместо f то, что дано, и f, разложенную на простейшие множители.
В отчете прокомментируйте результаты выдаваемые MatLab.
Для задачи в) обязательно сначала посчитать интегралы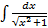 
, 
, 
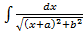вручную, затем вывести формулу для функции обратной гиперболическому синусу: 
.
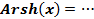Напоминаю, что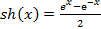 
.
Затем только вычислите эти интегралы с помощью int и сравните результаты.
Символьное вычисление определённого интеграла.При вычислении определённого интеграла в символьном виде следует задать значения нижнего и верхнего предела в качестве нижнего и верхнего предела в int(f,x,a,b).
Упражнение 2. Вычислить определённые интегралы в символьном виде:
а)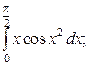 
б) 
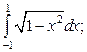в)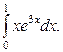 
Ж: В упражнении 2 сначала все посчитать вручную,
в пункте б) ответ должен быть pi/2, если MatLab выдает не символьное решение, а численное, то введите >> syms pi и снова посчитайте интеграл.
Следующую тему мы будем разбирать на 2-ом занятии, но попробуйте к ней подготовиться. На лекции вам начитают соответствующий материал. Или вы можете найти определения в книгах. В любом случае из всего, предложенного в оригинале задания уже к четвергу (у нас будет обычное занятие и вам это все равно на нем нужно будет это знать!)
Интегральные суммы и суммы Дарбу.
Упражнение 3. Создать М-функции, вычисляющие значения интегральных сумм на отрезке 
с равномерным разбиением на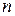 
отрезков для точек, взятых на:
а) левом, (к четвергу!)
Для самопроверки понимания понятия интегральной суммы и проверки работы М-функции возьмите функцию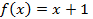 
на отрезке 
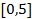при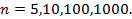 
И для этой же функции выполните часть Упражнение 4.: Создать М-функцию, вычисляющую значение нижней суммы Дарбу на отрезке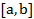 
с равномерным разбиением на 
отрезков.
Вычислите также интеграл 
и сравните с результатами, полученными через подсчет интегральной суммы.
В задачнике – это номер 7.320. Там же есть и теория. Но примеры 1 и 2, разбираемые в задачнике отличаются от того, что нужно сделать в Практикуме 1. Но понимать их все равно надо!
(остальное будем делать на 2-ом занятии)
Если М-функции не получится создать, то сделайте эту задачу вручную для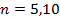 
к четвергу обязательно.
Также нужно сделать номера:7.356-7.363 (нечетные).
7.381,
7.455,7.478(сделать рисунок),7.484 (сделать рисунок), найти также площадь всех лепестков кривой 
. Внимание: у нас принято, что в полярной системе координат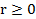 
. Поэтому количество лепестков у n-лепестковой розы соответствует n.
7.493,7.503, для задачи 7.484 найти длину кривой!
К понедельнику: М-функции, проверить работу М-функций для функциий 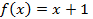на отрезке 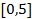и 
, на отрезке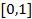 
для различных 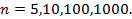Найдите также соответсвующий интеграл, сравните результат.
(остальное будем делать и обсуждать на 2-ом занятии в понедельник 20 февраля и сдавать 27 февраля.)
б) правом конце элемента разбиения;
с*) делящих их в произвольном заданном отношении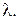 
Проверить работу М-функции для функции 
на отрезке 
при разбиении его на два равных элемента, пункт с) – деление отрезка пополам.
Упражнение 4. Создать М-функции, вычисляющие значения верхних и нижних сумм Дарбу на отрезке с равномерным разбиением на 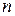отрезков. Проверить работу М-функции для функции на отрезке при разбиении его на два равных элемента.
Упражнение 5. Вычислить интегральные суммы и суммы Дарбу для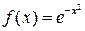 
на отрезке при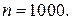 
4. Численное интегрирование. Функция quad(‘f’,a,b) вычисляет значения определенного интеграла функции f на отрезке с точностью до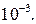 
Для повышения точности вычислений следует задать дополнительный четвёртый аргумент – требуемое значение точности.
Упражнение 6. Вычислить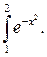 
Сравнить с результатами упражнении 5, вычислив разности между численным значением интеграла и интегральными суммами и суммами Дарбу.
