6.
6.1. Цель работы
Программа Excel не позволяет непосредственно строить графики функций, заданных формулами. В связи с этим целью лабораторной работы является изучение способов построения графиков функций с помощью таблиц подстановки.
6.2. Задания к выполнению лабораторной работы
Построить графики функций, заданных формулами y = ax + b и y = bax, коэффициенты которых определены в лабораторной работе №5. Значения независимой переменной x заданы в лабораторной работе №4. Построенные графики прямой и показательной функции, аппроксимирующие построенную в лабораторной работе №4 кривую, расположить на одном листе с этой кривой. Проанализировать результат аппроксимации.
6.3. Подготовка к работе
Для выполнения работы следует ознакомиться с примером действий для выполнения заданий, рассмотренным в разделе 6.4
6.4. Примеры действий для выполнения лабораторной работы.
Так как программа Excel не позволяет непосредственно строить графики функций, заданных формулами, необходимо сначала табулировать формулу, то есть создать таблицу значений функций для заданных значений переменной.
Сделайте текущей ячейку СЗ и занесите в нее значение 0. Эта ячейка будет использоваться как ячейка ввода, на которую будут ссылаться формулы.
Скопируйте все значений столбца А в столбец F, начиная с F2.

В ячейку G1 введите формулу =C3*$C$1+$D$1
В ячейку Н1 введите формулу =$D$2*$C$2^C3
Выделите прямоугольный диапазон, включающий столбцы F, G и Н и строки от строки 1, содержащей формулы, до последней строки с данными в столбце F.
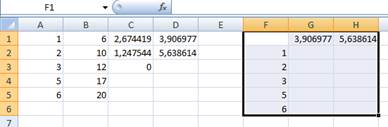
Дайте команду Данные - > Работа с данными -> Анализ «что-если» > Таблица данных. Выберите поле «Подставлять значения по строкам в:» и щелкните на ячейке ввода СЗ.
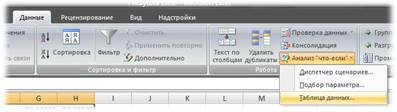
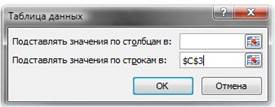
Щелкните на кнопке ОК.
В результате в ячейках G2:G6 и H2:H6 получим значения соответственно линейной и показательной функций для значений аргумента в ячейках F2:F6
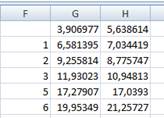
Поместим исходную кривую, созданную в лабораторной работе №4, на отдельном листе. Затем там же построим графики аппроксимирующих её прямой и показательной функции, значения которых получили выше.
Для этого щелкните по диаграмме, созданной в лабораторной работе №4, и выполните следующие действия:
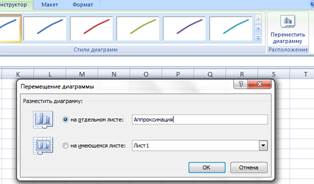
Конструктор -> Расположение -> Переместить диаграмму -> На отдельном листе > (Введите любое имя нового листа, например «Аппроксимация») и нажмите «Ок».
Кликните на диаграмме правой кнопкой мыши и нажмите “Выбрать данные”.


11. Затем нажмите “Добавить”. В поле «Имя» укажите: «Аппроксимация линейной функцией». В поле «Значения Х» укажите диапазон ячеек от F2 до F6, а в поле «Значения Y» укажите диапазон ячеек от G2 до G6.
12. Еще раз щелкните на кнопке “Добавить”. В поле «Имя» укажите: «Аппроксимация показательной функцией». В поле «Значения Х» укажите диапазон ячеек с данными от F2 до F6, а в поле «Значения Y» укажите диапазон ячеек от Н2 до H6.
13. Щелкните на кнопке «ОК», чтобы перестроить диаграмму в соответствии с новыми настройками.
14. Сохраните книгу examples.

6.1. Контрольные вопросы.
1. Можно ли непосредственно построить график функции, заданной формулой в среде Excel?
2. Что означает «табулирование» в среде Excel?
3. Как строятся графики на основе таблиц подстановок?
4. Как добавить к ранее построенной диаграмме дополнительный график?
Лабораторная работа №7
Решение уравнений средствами программы Microsoft Excel.
7.1. Цель лабораторной работы
Программа Excel позволяет находить приближенные значения корней уравнений численными методами. Целью данной работы является изучение методов решения уравнений средствами Microsoft Excel.
7.2. Задания к выполнению лабораторной работы
Решить выданные преподавателем уравнения в среде Microsoft Excel.
7.3. Подготовка к работе
Для выполнения работы следует ознакомиться с примером действий для выполнения заданий, рассмотренным в разделе 7.4
7.
7.1.
7.2.
7.3.
7.4. Примеры действий для выполнения лабораторной работы.
Программа Excel позволяет находить приближенные значения корней уравнений численным методом:
При решении уравнения с несколькими корнями следует осуществить несколько итераций для нахождения всех корней, т.к за одну итерацию численный метод позволяет найти только один корень. Нахождение соответствующего корня уравнения зависит от того, какое число было выбрано в качестве начального приближения к корню.
Пример действий для решения уравнения A2 - 8A=17 приведен ниже:
1. Запустите программу Excel (Пуск - > Все программы - > Microsoft Office->Microsoft Excel 2007) и откройте книгу examples, созданную ранее.
2. Создайте новый лист, дважды щелкните на его ярлычке и присвойте ему имя «Решение уравнения».
3. Занесите в ячейку А1 значение 0 (Начальное приближение к первому корню).
4. Занесите в ячейку В1 левую часть уравнения, используя в качестве независимой переменной ссылку на ячейку А1. Соответствующая формула может, например, иметь вид =A1*A1 - 8*A1
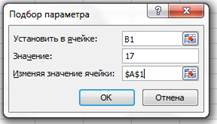
5. Дайте команду Данные > Анализ > Подбор параметра.

6. В поле «Установить в ячейке:» укажите В1, в поле «Значение:» задайте 17, в поле «Изменяя значение ячейки:» укажите А1.
8. Щелкните на кнопке ОК и посмотрите на результат подбора, отображаемый в диалоговом окне Результат подбора параметра. Щелкните на кнопке ОК, чтобы сохранить полученные значения ячеек, участвовавших в операции.

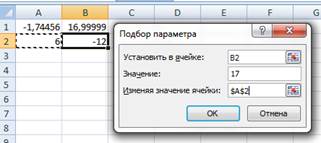
9. Повторите пункты 3 – 7 с ячейками A2 и B2 с другим начальным приближением для получения второго корня (начальное приближение 6).

Сохраните книгу examples.
7.4. Контрольные вопросы.
1. Какова последовательность действий для решения уравнений в среде Excel?
2. Можно ли найти все корни нелинейного уравнения за 1 итерацию?
3. От чего зависит количество итераций для нахождения корней уравнений?
8. Лабораторная работа №8
Решение задач оптимизации в среде Microsoft Excel.
8.1. Цель лабораторной работы
Целью лабораторной работы является изучение средств Excel для нахождения оптимальных решений (значений управляемых параметров) при заданных критерии эффективности и ограничениях.
8.2. Задания к выполнению лабораторной работы
Решить предложенную преподавателем задачу оптимизации средствами Microsoft Excel 2007.
8.
8.1.
8.2.
8.3. Подготовка к работе
Для выполнения работы следует ознакомиться с примером действий для выполнения заданий, рассмотренным в разделе 8.4
8.4. Примеры действий по выполнению заданий к лабораторной работе.
В качестве примера рассмотрим решение следующей задачи оптимизации.
Задача: завод производит электронные приборы трех видов (прибор А, прибор В, прибор С).
Для сборки используются микросхемы трех типов (тип1, тип2, тип3)
Стоимость изготовления приборов одинакова. Ежедневно на склад завода завозят по 500 микросхем типа1 и по 400 типа2 и типа3.
Дано (см. таблицу ниже) количество деталей каждого типа, требуемое для создания одного прибора класса A, класса B и класса C:
| Прибор А | Прибор В | Прибор С | |
| Тип1 | |||
| Тип 2 | |||
| Тип 3 |
Найти максимальное суммарное количество приборов различного вида (А, В и С), которое может произвести завод в день, если производственная мощность завода позволяет использовать запас поступающих микросхем полностью.
В этой задаче оптимизации независимыми (управляемыми) переменными (параметрами) от которых зависит критерий эффективности (целевая функция) и ограничения, являются количество приборов типа А, типа В и типа С, производимые в день. Целевой функцией (критерием эффективности) максимум которой ищется в задаче, является суммарное количество приборов трех типов, производимое в день. Ограничения связаны с необходимостью не превышать количество микросхем разных типов, поставляемых ежедневно.
Для решения задачи оптимизации необходимо ввести данные задачи в табличном виде, задать формулы ограничений, которые должны удовлетворять решению задачи, и задать формулу для целевой функции (критерия эффективности)
Примером решения этой задачи может быть приведенная ниже последовательность действий.
1. Запустите программу Excel (Пуск - > Все программы - > Microsoft Office->Microsoft Excel 2007) и откройте книгу examples, созданную ранее.
2. Создайте новый лист, дважды щелкните на его ярлычке и присвойте ему имя «Решение задачи оптимизации».
3. В ячейки А2, A3 и А4 занесите дневной запас комплектующих — числа 500,400 и 400, соответственно.
4. В ячейки С1, D1 и Е1 занесите нули — в дальнейшем значения этих ячеек будут подобраны автоматически. В ячейках С1, D1, E1 будут находиться значения, равные количеству приборов соответственно типов А, В, С, производимых в день.
5. В ячейках диапазона С2:Е4 разместите таблицу расхода комплектующих.
| Прибор А | Прибор В | Прибор С | |
| Тип1 | |||
| Тип 2 | |||
| Тип 3 |
6. В ячейках В2:В4 нужно указать формулы для расчета расхода комплектующих по типам. В ячейке В2 формула будет иметь вид =$C$1*C2+$D$1*D2+$E$1*E2, а остальные формулы можно получить методом автозаполнения (обратите внимание на использование абсолютных и относительных ссылок).
7. В ячейку F1 занесите формулу, вычисляющую общее число произведенных приборов: для этого выделите диапазон С1:Е1 и щелкните на кнопке «Автосумма» (Формулы ->Автосумма).
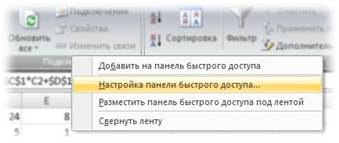
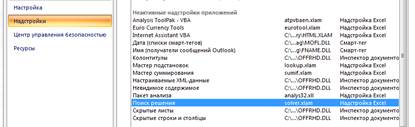
Для последующих действий нам потребуется команда «Поиск решения», но по умолчанию она отключена.Чтобы включить эту команду, необходимо проделать следующие действия:
àНа главной панели инструментов щелкнуть правой кнопкой мыши -> настройка панели быстрого доступа -> надстройки -> поиск решения (нажмите “Перейти”) ->(поставьте галочку напротив “поиск решения”) ->OK.

8. Выберите команду: Данные ->Поиск решения — откроется диалоговое окно Поиск решения.

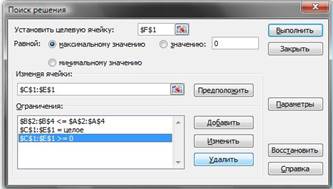
9. В поле «Установить целевую ячейку» укажите ячейку, содержащую оптимизируемое значение (F1). Установите переключатель Равной максимальному значению (требуется максимальный объем производства).
10. В поле Изменяя ячейки задайте диапазон подбираемых параметров — С1:Е1.

11. Чтобы определить набор ограничений, щелкните на кнопке «Добавить». В диалоговом окне «Добавление ограничения» в поле «Ссылка на ячейку» укажите диапазон В2:В4. В качестве условия задайте «<=». В поле «Ограничение» задайте диапазон А2:А4. Это условие указывает, что дневной расход комплектующих не должен превосходить запасов. Щелкните на кнопке «ОК».

12. Снова щелкните на кнопке «Добавить». В поле «Ссылка на ячейку» укажите диапазон С1:Е1. В качестве условия задайте >=. В поле «Ограничение» задайте число 0. Это условие указывает, что число производимых приборов неотрицательно. Щелкните на кнопке «ОК».
13. Снова щелкните на кнопке «Добавить». В поле «Ссылка» на ячейку укажите диапазон «С1:Е1». В качестве условия выберите пункт «цел». Это условие не позволяет производить доли приборов. Щелкните на кнопке «ОК».
14. Щелкните на кнопке «Выполнить». По завершении оптимизации откроется диалоговое окно «Результаты поиска решения».
15. Установите переключатель «Сохранить найденное решение», после чего щелкните «ОК».
16. Сохраните рабочую книгу examples.

8.3. Контрольные вопросы.
1. Как формулируется задача оптимизации в табличном виде?
2. Как формулируются критерий эффективности и ограничения, которым должно удовлетворять решение?
3. Какие программы Excel используются для нахождения оптимальных значений независимых(управляемых) переменных и соответствующего значения целевой функции?
Литература
1. «Информатика. Базовый курс» под ред. Симоновича С.В. Питер, 2010 г.
2. «Excel 2007» Пащенко И.Г., Москва, «Эксмо», 2009 г.






