Линией тока называется линия, касательная к каждой точке которой совпадает по направлению с вектором скорости в данный момент времени.
Если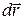 
– элемент линии тока, то из условия, что на линии тока ║ 
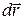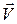, можно записать следующие уравнения:
(2.5)
которые являются дифференциальными уравнениями линий тока.
Семейство линий тока дает картину течения в данный момент времени, можно сказать, моментальный снимок направлений скоростей потока.
Через каждую точку пространства может проходить множество траекторий частиц, они могут пересекаться и пересекать сами себя.
Линии тока не пересекаются ни сами с собой, ни с другими линиями тока, так как вектор скорости в одной точке пространства не может иметь два разных значения в данный момент времени. Исключение составляют лишь особые точки, в которых скорость V = 0 (критические точки или точки
Необходимо четко представлять разницу между линией тока и траекторией движения частицы. Если траектория отражает изменение положения частицы с течением времени, то линия тока указывает направление скоростей разных частиц в один и тот же момент времени. И только при установившемся движении линия тока совпадает с траекторией частицы. В этом случае траектории всех частиц, проходящих через какую-либо точку пространства, будут одинаковыми, следовательно, в каждый момент времени все частицы, которые лежат на траектории, будут образовывать и линию тока. В случае неустановившегося движения линии тока и траектория частицы не совпадают.
7. Метод Эйлера изучения течений жидкости. Системы координат, применяемые при исследовании течений жидкости.
Метод Эйлера.В методе Эйлера исследуют поля векторных и скалярных параметров движущейся жидкости, не рассматривая вопрос о том, как движется та или иная частица.
При неустановившемся движении каждому моменту времени соответствует своё поле скоростей в рассматриваемой области движения жидкости. Полное описание процесса достигается в том случае, когда определены скорости во всех точках области за весь период наблюдения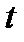 
. Это можно представить как серию последовательных кадров поля скоростей, полученного киносъёмкой. Если для данной системы координат 
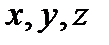определены функции, описывающие изменение поля скоростей и давления во времени
| (3.2) |
,
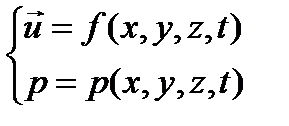то этим решена одна из основных задач гидродинамики – установлен закон распределения скоростей и давлений в потоке.
Таким образом, исследуют поля векторных и скалярных параметров движущейся жидкости, не рассматривая вопрос о том, как движется та или иная частица.
Оба метода исследования жидкости – и метод Лагранжа и метод Эйлера математически связаны между собой и возможен переход от уравнений (3.1) к уравнениям (3.2). Как показало развитие гидравлики, в большинстве случаев метод Лагранжа более сложен и трудоёмок, чем метод Эйлера. Поэтому далее в основном рассматривается решение задач движения жидкости на основе метода Эйлера.
Однако задача отыскания функций скорости и давления методом Эйлера также является весьма сложной. Даже заменяя реальную жидкость моделью «идеальной жидкости», решить её в большинстве случаев не представляется возможным.
Поэтому в технической гидродинамике идут по иному пути и используют так называемый «гидравлический метод». Гидравлический метод (метод технической гидродинамики) основан на использовании некоторых осреднённых и интегральных характеристик потока.
В основу этого метода полагают уравнения, которые существенно отличаются от системы уравнений в методе Эйлера. К числу таких основных уравнений гидравлики относятся следующие:
- уравнение несжимаемости и неразрывности для потока жидкости (уравнение расхода);
- уравнение кинетической энергии для потока реальной жидкости (уравнение Бернулли);
- уравнение количества движения для потока реальной жидкости;
- эмпирические и полуэмпирические зависимости (Дарси и Вейсбаха) для оценки работы сил трения, возникающих в реальной жидкости.
Используя данные уравнения в сочетании с некоторыми приёмами рассмотрения гидравлических явлений (линия тока, средняя скорость и др.) получаем законченную техническую теорию, позволяющую с приемлемой точностью решать большой круг практических задач, относящихся к механике реальной жидкости.
