ОПРЕДЕЛЕНИЕ ОТНОСИТЕЛЬНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ТВЕРДЫХ ДИЭЛЕКТРИКОВ
Преподаватель Студенты гр.355
Орловская А.В. Полынцев Е.
«23» мая 2016 г. Власов А.
«23» мая 2016 г.
ВВЕДЕНИЕ
Целью данной работы является изучение явления поляризации и экспериментальное определение величины относительной диэлектрической проницаемости в твердых изоляторах.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Схема, используемая для измерений, изображена на рис. 1.1 и включает в себя генератор синусоидального сигнала, RC –цепочку и осцилограф для измерения амплитуды входного и выходного сигналов. R = 62 кОм. Конструктивно схема размещена в настольном макете, в правой стороне его наклонной части. Роль генератора и осциллографа выполняет компьютер.
Переключение осциллографа на измерение входного либо выходного сигналов производится тумблером S2 на панели. Конденсатор представляет собой две параллельные металлические пластины площадью 100 см2, между которыми помещается пластина твердого диэлектрика. Диэлектрическая пластина вставляется в щель на правой стенке макета. Для облегчения измерений диэлектрическая пластина разлинована на участки площадью по 10 см2 каждый.

Рисунок 1.1 - Схема рабочего узла, используемого для проведения эксперимента.
Методика измерений:
Наблюдаем изменение амплитуды выходного сигнала при вытягивании
диэлектрической пластины из конденсатора. Измеряем зависимость коэффициента передачи К от величины удаленной (вытянутой) площади Sуд. Рассчитываем емкость. Строим графики зависимости С от Sуд. По наклону прямых определяем диэлектрическую проницаемость диэлектрика.
2. ОСНОВНЫЕ РАСЧЁТНЫЕ ФОРМУЛЫ
Электрический дипольный момент:
 (2.1)
(2.1)
q- заряд,
l- расстояние между зарядами.
Установлено, что каждая молекула будет обладать электрическим дипольным моментом:
 (2.2)
(2.2)
α - поляризуемость молекулы,
E -напряженность электрического поля в месте нахождения молекулы внутри диэлектрика.
Вектор поляризации (дипольный момент единицы объема) равен:
 (2.3)
(2.3)
n - концентрация молекул,
α - поляризуемость молекулы.
Емкость плоского конденсатора равна:
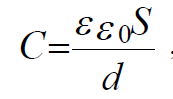 (2.4)
(2.4)
 - относительная диэлектрическая проницаемость,
- относительная диэлектрическая проницаемость,
 - электрическая постоянная,
- электрическая постоянная,
S - площадь обкладки конденсатора,
d - расстояние между обкладками.
Или
 (2.5)
(2.5)
Круговая частота  равна
равна
 (2.6)
(2.6)
Коэффициент передачи К:
 (2.7)
(2.7)
Диэлектрическая проницаемость равна:
(2.8)
Формулы расчёта погрешностей:
 (2.9)
(2.9)
РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Таблица 3.1 – Результаты прямых и косвенных измерений
| Название диэлектрика | № | S, см2 | Uвх, В | Uвых, В | К | С, пФ | d, мм | Примечания |
| Стекло-текстолит | 3,77 | 0,54 | 0,149 | 0,79 | 

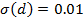 мм мм


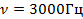
| |||
| 6,5 | 0,53 | 0,146 | ||||||
| 0,51 | 0,135 | |||||||
| 19,5 | 0,48 | 0,127 | ||||||
| 0,45 | 0,119 | |||||||
| 32,5 | 0,42 | 0,111 | ||||||
| 0,39 | 0,103 |
Рисунок 3.1 – График зависимости электроемкости от удаленной площади диэлектрика
По формуле (2.5) рассчитаем емкость конденсатора для каждого измерения:


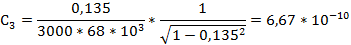


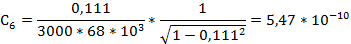
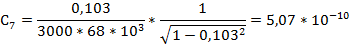
ЗАКЛЮЧЕНИЕ






