Кафедра специализированных компьютерных систем
РАСЧЁТНАЯ ГРАФИЧЕСКАЯ РАБОТА
по дисциплине "Дискретная математика"
Выполнил: Турчанинов Г.И.
Группа: КВ-22
Номер зачетной книжки: КВ-2219
Вариант: 28
2 семестр 2012/2013 уч. года
Задание №1
Решить уравнение в алгебре отношений. При решении использовать алгебраический метод. В качестве неизвестного принимается множество, обозначенное символом В.
Базовое уравнение: 
Где значение: 
(Символ 
означает операцию «симметрическая разность»)
Решение:
Упростим базовое уравнение:
Подставим: 
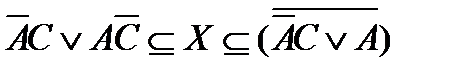
При: 
Ответ:
Задание №2
Граф задан матрицей смежности:
R= 
Представим орграф графически:
| X1 |
| X3 |
| X4 |
| X5 |
| X6 |
| X7 |
| X8 |
| X2 |
Выполнить разложение орграфа на компоненты сильной связности методом Мальгранжа - Томеску
Решение:
Дополняем матрицу смежности R слева столбцом прямого транзитивного замыкания 
и снизу строкой обратного транзитивного замыкания 
.
Заполняем их по определенному алгоритму и находим компоненты сильной связности C(xi) по формуле: 
.
| ||||||||||||
| ||||||||||||
Найти методами Магу все внутренне устойчивые множества вершин графа, все внешне устойчивые множества вершин графа, ядра графа.
Решение:
Найдем все внутренне устойчивые множества вершин графа методом Магу:
(1Ú67)(2Ú1456)(3Ú25)(4Ú12356)(5Ú28)(6Ú1257)(7Ú5)(8Ú5)=(12Ú1456Ú267Ú
Ú1457)(34Ú12356Ú245Ú12356)(56Ú1257Ú268Ú12578)(78Ú57Ú58Ú5)=
=(1234Ú12356Ú1245Ú13456Ú123456Ú12456Ú23467Ú123567Ú24567)(5678Ú
Ú56Ú12578Ú1257Ú2678Ú2568)=123456Ú123457Ú1234678Ú12356Ú123567Ú
Ú1235678Ú12456Ú12457Ú1245678Ú13456Ú1234567Ú12345678Ú234567Ú
Ú1234567Ú234678Ú24567Ú124567Ú245678=12356Ú12456Ú12457Ú13456Ú
Ú234678Ú24567
Ответ:
Инвертируя каждое полученное множество, получим внутренне устойчивые множества:
X4,x7,x8 }; { x3,x7,x8 }; { x3,x6,x8 }; {x2,x7,x8}; {x1,x5}; {x1,x3,x8}.
Число внутренней устойчивости графа a(G)=3.
Найдем все внешне устойчивые множества вершин графа методом Магу:
(1Ú2Ú4Ú6)(2Ú3Ú4Ú5Ú6)(3Ú4)(4Ú2)(5Ú2Ú3Ú4Ú6Ú7Ú8)(6Ú1Ú2Ú4)(7Ú1Ú6)(8Ú5)=
= (34Ú23Ú4Ú24)(78Ú57Ú18Ú15Ú68Ú56) = 2378Ú2357Ú1238Ú1257Ú2368Ú2356Ú
Ú478Ú457Ú148Ú145Ú468Ú456
Ответ:
Внешне устойчивые множества:
{ x2,x3,x7,x8 }; { x2,x3,x5,x7 }; { x1,x2,x3,x8 }; { x1,x2,x3,x5}; { x2,x3,x6,x8 };
{ x2,x3,x5,x6}; { x4,x7,x8 }; { x4,x5,x7 }; { x1,x4,x8 }; { x1,x4,x5 }; { x4,x6,x8 };
{ x4,x5,x6 };
Число внешне устойчивости графа b(G)=3.
Ядро графа: { x4,x7,x8 } – одновременно максимально внутренне устойчивое множество вершин графа, и минимально внешне устойчивое множество вершин графа)
Найти цикломатическое число и построить матрицу фундаментальных циклов графа. Построить три нефундаментальных цикла графа.
Решение:
Перейдём от орграфа к неографу и зададим его графически.
X1
X3
X5
X6
X7
X8
X4
X2
| X6 |
| X5 |
| X7 |
| X8 |
| X1 |
| X2 |
| X3 |
| X4 |
Цикломатическое число n(G)=m-n+1=17-8+1=10,
где m — количество ребер неографа, n — количество вершин неографа.
(m-n+1 — число рёбер, не вошедших в остов, а также количество фундаментальных циклов)
ÞМаксимальное количество фундаментальных циклов графа равно n(G)=10, а максимальное количество всех циклов графа равно 2n(G)-1=1023.
Матрица фундаментальных циклов графа:
| F1 | |||||||||||||||||
| F2 | |||||||||||||||||
| F3 | |||||||||||||||||
| F4 | |||||||||||||||||
| F5 | |||||||||||||||||
| F6 | |||||||||||||||||
| F7 | |||||||||||||||||
| F8 | |||||||||||||||||
| F9 | |||||||||||||||||
| F10 |
Три нефундаментальных цикла графа:
| F1ÅФ5 | ||||||||||||||||||
| F2ÅФ7 | ||||||||||||||||||
| F3ÅФ10 |
F2ÅФ7:
2
13
15
7
11
16
F3ÅФ10:
13
10
11
