Тангенциальное уравнение прямой на плоскости:
Числа 
и 
называются её тангенциальными, линейными или плюккеровыми координатами.
Плоскость
Плоскость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается заодно из исходных понятий, которое лишь косвенным образом определяется аксиомам геометрии.
Плоскость — это поверхность, образованная кинематическим движением образующей по направляющей, представляющей из себя прямую (начертательная геометрия).
Свойства плоскости
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Две плоскости являются либо параллельными, либо пересекаются по прямой.
- Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
- Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
- Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.
Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.
Уравнения плоскости
Впервые встречается у А. К. Клеро (1731).
Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).
Нормальное уравнение ввёл Л. О. Гессе (1861).
Плоскость — алгебраическая поверхность первого порядка: в декартовой систем координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
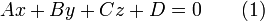
где 
и 
— постоянные, причём 
и 
одновременно не равны нулю; в векторной форме:
где 
— радиус-вектор точки 
, вектор 
перпендикулярен к плоскости (нормальный вектор). Направляющие косину вектора 
:
Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При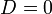 
плоскость проходит через начало координат, при 
(или 
, 
) П. параллельна оси 
(соответственно 
или 
). При 
(
, или 
) плоскость параллельна плоскости 
(соответственно 
или 
).
- Уравнение плоскости в отрезках:
где 
, 
, 
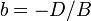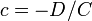— отрезки, отсекаемые плоскостью на осях 
и .
- Уравнение плоскости, проходящей через точку
перпендикулярно вектору нормали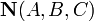 
:
в векторной форме:
· Уравнение плоскости, проходящей через три заданные точки 
, не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где 
- единичный вектор, 
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
