Вариант №33
Свойства групп. Элемент симметричный к симметричному, симметричный к а*в.
Свойства групп.
Прежде чем приводить другие примеры групп укажем некоторые простейшие свойства этих алгебраических систем. Во всех последующих формулировках считается, что x, y, z,... - элементы некоторой группы G.
1. Закон сокращения
(левое сокращение)
(правое сокращение)
Докажем, например, первый закон. Используем существование обратного элемента 
и свойство ассоциативности операции.
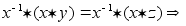
y=z.
2. Единственность нейтрального элемента
В любой группе нейтральный элемент определен однозначно. В самом деле, если 
и 
оба являются нейтральными, то по определению
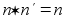и в то же время 
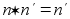, откуда 
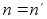. Единственный нейтральный элемент группы G будет в дальнейшем обозначаться 
или просто e.
3. Единственность обратного элемента
Для каждого элемента x обратный элемент определен однозначно. В самом деле, если элементы y и z являются обратными для x, то y*x=e и z*x=e, откуда y*x=z*x и по закону сокращения y=z.
4. Признак нейтрального элемента
Действительно, поскольку 
, имеем 
, откуда по закону сокращения получаем 
.
5. Разрешимость любого уравнения первой степени (существование обратной операции)
. Элемент z определен однозначно. (Его можно назвать «частным» от деления y на x).
Имеем: 
и значит можно взять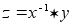 
. Однозначность следует из закона сокращения: 
.
Вариант №34
Многочлены степени n и степени не выше n. Проверка выполнимости для них групповых свойств.
Многочлен Pn(x) относительно переменной x вида
Pn(x) = a0·xn + a1·xn-1+ a2·xn-2+ … + an-1·x+ an, (1),
многочлен коэффициент степень разложение
где a0, a1, a2… an - действительные числа и a0 0, называется многочленом, расположенным по убывающим степеням x, или многочленом, представленном в каноническом виде.
Числа a0, a1, a2… an называются его коэффициентами, одночлен a0·xn - называют старшим членом, а число n-степенью многочлена.
Если у многочлена, представленного в каноническом виде, отсутствует некоторая степень x, то коэффициент соответствующего одночлена равен нулю.
Два многочлена, представленные в каноническом виде, тождественно равны, если равны их степени и равны коэффициенты при одинаковых степенях x.
Пример. Найти числа если многочлен x3+6x2+x+ является кубом двучлена x+.
Решение. Используя определение тождественного равенства двух многочленов, получаем систему:
откуда
Если многочлены Рn(x), Qm(x), и Kl(x) таковы, что справедливо тождественное равенство
то говорят, что каждый из многочленов и является делителем многочлена При этом говорят, что многочлен делится (нацело) на многочлен (или, и тогда многочлен (соответственно) называют частным от деления многочлена на многочлен (соответственно.
Доказывается, что если многочлен степени n делится на многочлен степени m, то частным от деления будет многочлен степени n-m и этот многочлен единственный.
Отсюда следует, что если многочлен степени n делится на многочлен степени n, то, где, т.е. коэффициенты этих многочленов пропорциональны. Например если известно, что многочлен 2x2+b·x+c делится на многочлен x2-x+1, то b= -2 и c=2.
