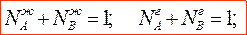Законы Гиббса-Коновалова устанавливают связь между составом жидкого раствора и составом насыщенного равновесного с ним пара в зависимости от температуры и давления.В равновесной двухкомпонентной системе сумма мольных долей компонентов в жидкой и паровой фазах равны единице:
Законы Гиббса-Коновалова и предыдущее уравнение справедливы для двухкомпонентных смесей, состоящих из летучих компонентов.Равновесие между раствором и паром удобно рассма-тривать в виде диаграмм, выражающих зависимость температуры жидкой смеси от ее состава.
1-закон Гиббса-Коновалова
В условиях равновесия относительное содержание компонента в паровой фазе отличается от содержания этого компонента в жидком растворе.В паре содержание больше того компонента, добавление которого в раствор понижает температуру кипения или повышает давление насыщенных паров.Пар обогащается более летучим компонентом. При постоянном давлении температура кипения раствора возрастает при увеличении концентрации компонента, содержание которого в паре меньше, чем в растворе. При постоянной температуре давление пара над раствором при увеличении концентрации компонента, содержание которого в паре больше, чем в растворе.
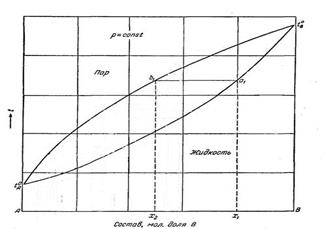
Диаграммы состава «жидкость-пар» двухкомпонент-ной системы при постоянном давлении (а) и постоянной температуре (б).
I-паровая фаза; II -пар+жидкость; III - жидкая фаза.
2-закон Гиббса-Коновалова
Точки экстремума на кривых температуры кипения (P=const) или на кривых давления (T=const) соответствуют растворам, состав которых одинаков с составом равновесного с ней пара. Нераздельнокипящие смеси называют азеотропными смесями. В условиях равновесия азеотропные смеси испаряются как чистое вещество.В азетропных смесях в точках экстремума
Законы Гиббса-Коновалова справедливы вдали от критического состояния двухфазной системы.
Диаграммы состава «жидкость-пар» двухкомпонент-ной системы с азеотропными точками при постоянном давлении (а) и постоянной температуре (б).
I-паровая фаза; II -пар+жидкость; III - жидкая фаза.
Термодинамическое обоснование законов Гиббса-Коновалова
Отношение между долями компонентов в паровой и жидкой фазах выражается следующим уравнением:
Уравнение показывает изменение состава жидкости и пара в соответствити с закономами Гиббса-Коновалова.К термодинамическому обоснованию законов Гиббса-Коновалова можно подойти, используя уравнение Дюгема-Маргулиса.
 |
Уравнение Дюгема-Маргулиса позволяет определить связь между изменением парциального давления компонентов (рА, рВ) и составвом раствора (NAЖ). С его помощью можно рассчитать давление пара одного из компонентов раствора, если известны давление пара другого компонента и состав раствора.Уравнение Дюгема-Маргулиса справедливо для любого неидеального двухкомпонентного жидкого раствора, образованного летучими компонентами.Уравнение Дюгема-Маргулиса позволяет определить изменение общего давления системы в зависимости от мольной доли более летучего компонента, которое равно:
Перегонка (дистилляция) и ректификация
Соотношение между жидкой и паровой фазами в гетерогенной области II диаграммы состава двухкомпонентной системы находят по правилу рычага.
Правило рычага:
Отрезки на прямой, соединяющей на диаграмме состава двухкомпонентной системы паровую и жидкую фазы, отсекаемые определенной точкой на этой прямой, обратно пропорционально числу молей каждой из фаз. при температуре tкип правило рычага записывается следующим образом:
Дистилляцией или дробной перегонкой называют разделение жидких растворов, основанное на отличии состава жидкости от состава образующегося из нее пара.Дистилляция осуществляется путем частичного испарения и последующей конденсации пара.Отгонная фракция (дистиллят) обогащена более летучим (низкокипящим) компонентом, а неотогнанная жидкость (кубовой остаток, конденсат) обогащена менее летучим (высококипящим) компонентом.Количественно оценку дистилляции проводят при помощи коэффициента разделения a:
В простейших системах a не зависит от состава системы и равен
 |
Твердые растворы
Твердыми растворами называют однородные системы, состоящие из двух и более твердых компонентов.Способность образовывать твердые растворы свойственны всем кристаллическим твердым телам.В большинстве случаях твердые растворы образуются в узком интервале концентрации, значительно реже в широком интервале концентрации. Примеры: золото для ювелирных изделий (Au-Cu), драгоценные природные камни, слюда, полевые шпаты, сплавы металлов, сталь, чугун, латунь и др. В зависимости от способа получения и особенности взаимодействия компонентов твердые растворы делятся на растворы:1)замещения; 2) внедрения и 3) вычитания. Твердые растворы замещения образуются в результате замещения молекул, атомов и ионов в кристаллических решетках растворителя на молекулы, атомы и ионы растворенного вещества. Твердые растворы замещения образуют элементы, атомные радиусы которых отличаются не более чем на 15 %. К ним можно отнести сплав Cu-Ni. Твердые растворы внедрения образуют атомы радиусы которых существенно отличаются друг от друга.Такие растворы образуются когда неметаллы (бор, водород, кислород, азот, углерод) в металлах. К ним относятся чугун, сталь и др. В твердых растворах вычитания происходит «выпадение» атомов из кристаллической решетки. Такие системы иногда называют твердыми растворами с дефектами решетки. В зависимости от взаимной растворимости компонен-тов твердые растворы делятся на неограниченные и ограниченные твердые растворы. В зависимости от растворимости компонентов раство-ра различают системы,
1) компоненты которых взаимно неограниченно раствори-мы в жидком и твердом состоянии,
2) компоненты которых растворимы лишь в жидком состоянии, а в твердом состоянии не образуют раство-ры (растворы с эвтектикой).
