В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения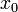 
, а затем использовать это значение на каждой последующей итерации:
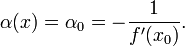
При таком выборе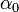 
в точке 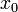выполнено равенство:
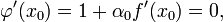
и если отрезок, на котором предполагается наличие корня 
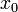и выбрано начальное приближение , достаточно мал, а производная 
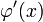непрерывна, то значение 
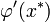будет не сильно отличаться от 
и, следовательно, график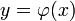 
пройдёт почти горизонтально, пересекая прямую 
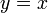, что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число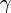 
следует выбрать равным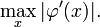 
Пример метода Ньютона(касательных) на рисунке 13.
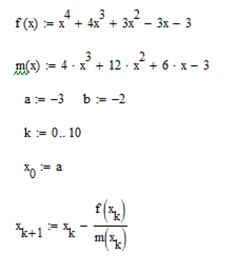
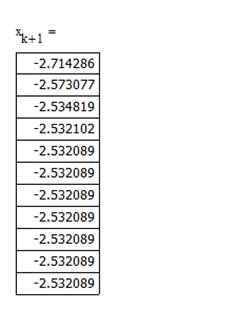
Рис. 13. М етод Ньютона (касательных).
Метод простых итераций
Для того, чтобы решить уравнение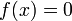 
, пользуясь методом простой итерации, необходимо привести его к виду 
, где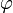 
– сжимающее отображение. Чтобы отображение было наиболее эффективно, необходимо, чтобы в точке очередной итерации выполнялось 
. Будем искать решение данного уравнения в виде 
, тогда:
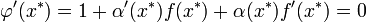
Воспользуемся тем, что 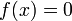, и получим окончательную формулу для 
:
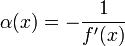
С учётом этого сжимающая функция примет вид:
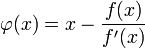
Тогда алгоритм нахождения численного решения уравнения 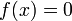сводится к итерационной процедуре вычисления:
Пример метода МПИ на рисунке 13.
Метод секущих
Метод Ньютона имеет множество усовершенствований и модификаций, при этом принято считать, что наиболее эффективной модификацией является метод секущих, дающий существенное ускорение сходимости приближенной последовательностей корней к точному корню по сравнению с самим методом Ньютона.
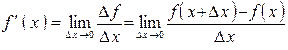
Рис.13. М етод МПИ.
При 
достаточно малым можно считать что выполнено приближенное равенство в точке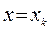 
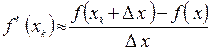
Подставляя данное в приближенное равенство в формулу метода Ньютона получим:
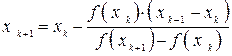
Из данного соотношения, имеющего трудность применения на практике связано с тем что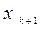 
есть как в левой так и в правой части, можно получить:
, 
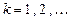
Данная формула дает метод секущих который отличается от предыдущих методов, тем что для подсчета приближенного значения корня нужно, знать ни одно приближение предыдущего значения, а целых 2 предыдущих значения, т.е. для вычисления требуется знание 
и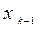 
. Такие методы называют двухшаговые, предыдущие методы хорд и касательных были одношаговыми. Применение полученной формулы на первом шаге невозможно, поэтому недостающее приближение на старте метода можно рассчитать методом Ньютона и лишь после этого можно применить метод секущих.
Пример метода секущих на рисунке 14.
Рис. 14. М етод секущих.
ЗАКЛЮЧЕНИЕ
Изучив основные функции MathCad, можно сделать вывод, что данная программа выполняет множество функции и ориентирована на людей различных профессий.
В соответствии с проблемами реальной жизни, математикам приходится решать одну или несколько из следующих задач:
- ввод на компьютере разнообразных математических выражений (для дальнейших расчетов или создания документов, презентаций, Web-страниц);
- проведение математических расчетов;
- подготовка графиков с результатами расчетов;
- ввод исходных данных и вывод результатов в текстовые файлы или файлы с базами данных в других форматах;
- подготовка отчетов работы в виде печатных документов;
- подготовка Web-страниц и публикация результатов в Интернете;
- получение различной справочной информации из области математики.
Для решения этих и других задач достаточно просто вводить математические выражения с помощью встроенного редактора формул, причем в виде, максимально приближенном к общепринятому, и тут же получать результат. Применение MathCad не только сократит время решения, но и поможет сравнить результаты различных методов. Благодаря этому наглядно будет видна погрешность, что позволит сравнить методы и выбрать оптимальный. Кроме того, можно изготовить на принтере печатную копию документа или создать страницу в Интернете именно в том виде, который этот документ имеет на экране компьютера при работе с Mathcad.
В процессе исследования нами были рассмотрены методы решения нелинейных уравнений и разработаны алгоритмы их решения в программе MathCad. Таким образом, задачи, которые мы ставили в своем исследовании, были решены.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ:
1. http://www.psn.izido.ru. Уроки «Основы работы в MathCad».
2. Работа в MathCAD. Пискунов В. В.:
http:// www.elib.ispu.ru/library/lessons/pekunov/index.html
3. Он-лайн самоучитель по MathCAD 14: http://www.computerbooks.ru/books/Mathematic/Book.MathCAD12/Menu.html
4. Учебник по MathCAD 14. Кирьянов В. Д.:
http:// www.maxp.kuzstu.ru/files/informatika/mathcad2001/INDEX.HTM
5. MathCAD Help. Файл
http://www.bookz.ru/authors/avtor-neizvesten-3/mathcadhelp.html
6. Учебник «Простейшие вычисления с помощью пакета MathCAD». http://www.bookz.ru/authors/avtor-neizvesten-3/mathcadprost.html
7. Официальный сайт РТС, производителя Mathcad: http://www.pts-russia.com/products/mathcad.htm
8. Библиотека ресурсов по системе MathCAD. Книги, электронные книги MathCAD, файлы MathCAD, галереи графики и анимаций, головоломки (сайт на английском языке): http://www.mathcad.com/library/
9. Образовательный математический сайт: http://www.exponenta.ru/
10. Учебно-методический комплекс "Численные методы с системой MathCAD для изучения алгоритмов решения математических задач с использованием системы MathCAD".
http:// www.petrsu.karelia.ru/psu/Deps/IMO/Complex/
