Основные формулы комбинаторики
В данном разделе мы займёмся подсчётом числа «шансов». О числе шансов говорят, когда возможно несколько результатов какого-либо действия (извлечение карты из колоды, подбрасывание кубика или монетки). Число шансов — это число способов проделать это действие или, что то же самое, число возможных результатов этого действия.
Теорема о перемножении шансов
Пусть одно действие можно проделать пятью способами, а другое — двумя. Каким числом способов можно проделать пару этих действий?
Теорема 1. Пусть множество 
состоит из 
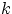элементов: 
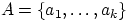, а множество 
— из 
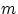элементов: 
. Тогда можно образовать ровно 
пар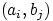 
, взяв первый элемент из множества , а второй — из множества .
Замечание 1. Можно сформулировать утверждение теоремы 1 так: если первый элемент можно выбрать 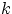способами, а второй элемент — 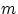способами, то пару элементов можно выбрать способами.
Доказательство. С элементом 
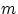мы можем образовать пар: 
. Столько же пар можно составить с элементом 
, столько же — с элементом 
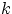и с любым другим из элементов множества . Т.е. всего возможно пар, в которых первый элемент выбран из множества , а второй — из множества .
QED
Упражнение 1. С помощью теоремы 1 доказать, что:
а)
при подбрасывании трёх монет возможно 2·2·2=8 различных результатов;
б)
бросая дважды игральную кость, получим 6·6=36 различных результатов;
в)
трёхзначных чисел бывает 9·10·10=900;
г)
трёхзначных чисел, все цифры которых различны, существует 9·9·8;
д)
чётных трёхзначных чисел возможно 9·10·5.
Урны и шарики
Есть урна (ящик), содержащая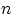 
пронумерованных объектов (шаров). Мы выбираем из этой урны 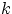шаров; результатом выбора является набор из 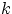шаров. Нас интересует, сколькими способами можно выбрать 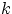шаров из 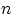, или сколько различных результатов может получиться. На этот вопрос нельзя дать однозначный ответ, пока мы не определимся: а) с тем, как организован выбор (можно ли шары возвращать в урну), и б) с тем, что понимается под различными результатами выбора.
Рассмотрим следующие возможные способы выбора.
1.
Выбор с возвращением: каждый вынутый шар возвращается в урну, каждый следующий шар выбирается из полной урны. В полученном наборе из 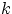номеров шаров могут встречаться одни и те же номера.
2.
Выбор без возвращения: вынутые шары в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера.
Условимся, какие результаты выбора (наборы из 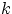номеров шаров) мы будем считать различными. Есть ровно две возможности.
1.
Выбор с учётом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трёх шаров из урны, содержащей 5 шаров, наборы (1, 5, 2), (2, 5, 1) и (4, 4, 5) различны, если порядок учитывается.
2.
Выбор без учёта порядка: два набора номеров шаров считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми.
Так, наборы (1, 5, 2) и (2, 5, 1) не различаются и образуют один и тот же результат выбора, если порядок не учитывается.
Подсчитаем, сколько возможно различных результатов для каждой из четырёх схем выбора (выбор с возвращением или без, и в каждом из этих случаев — с учётом порядка или без).
Упражнение 2. Перечислить все возможные результаты в каждой из четырёх схем при выборе двух шаров из четырёх. Например, при выборе с возвращением и без учёта порядка: (1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4).
Выбор без возвращения, с учётом порядка
Теорема 2. Общее количество различных наборов при выборе 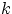элементов из 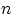без возвращения и с учётом порядка равняется
и называется числом размещений из 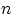элементов по 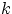элементов.
Доказательство. Первый шар можно выбрать 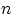способами, его номер — любой из 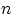возможных. При любом выборе первого шара есть 
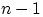способ выбрать второй шар. По теореме 1, число возможных пар
равно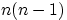 
. Для каждой такой пары есть 
способа выбрать третий шар. По теореме 1, число возможных троек
равно произведению числа пар 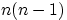и числа способов выбора третьего шара, т.е. равно 
. Продолжая рассуждения, получим, что общее число возможных наборов из 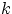шаров равно 
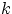. В этом произведении сомножителей последний множитель 
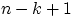есть число способов выбора 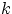-го шара, когда уже выбраны предыдущие.
QED
Следствие 1. Если в множестве 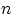элементов, то существует ровно 
перестановок этих элементов.
Доказательство. Перестановка — результат выбора без возвращения и с учётом порядка 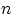элементов из 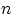. Поэтому общее число перестановок равно 
QED
Упражнение 3. Найти, сколько всего возможно различных результатов в следующих экспериментах:
а)
из колоды в 36 карт без возвращения, с учётом порядка вынимают три карты;
б)
Вася, Петя, Оля и Лена занимают какие-то четыре из десяти мест в классе;
в)
из русского алфавита выбирают четыре разные буквы и составляют слово;
г)
из различных цифр, не равных нулю, составляется трёхзначное число.
