Расчетно-графическая работа
по предмету
«Техническая термодинамика»
Выполнил:
студент 2 курса
ТЭФ, гр. ТП-42
Гречаный Андрей
Проверил:
Трокоз Я.Е.
Киев-2005
Содержание задания
 V=8м3 водяного пара при давлении P1=4 бар и температуре t1=200 °C совершают адиабатный процесс до давления P2=0,4 бар. Определить все начальные и конечные параметры рабочего тела, работу и количество тепла в процессе. Как изменятся результаты расчёта, если при тех же исходных данных этот процесс совершается с идеальным газом Н2Опри теплоёмкости, зависящей от температуры?
V=8м3 водяного пара при давлении P1=4 бар и температуре t1=200 °C совершают адиабатный процесс до давления P2=0,4 бар. Определить все начальные и конечные параметры рабочего тела, работу и количество тепла в процессе. Как изменятся результаты расчёта, если при тех же исходных данных этот процесс совершается с идеальным газом Н2Опри теплоёмкости, зависящей от температуры?
| Дано: V=8м3 P1=4 бар t1=200 °C P2=0,4 бар |
| h1, h2, s1, s2, u1, u2, Δu, Δh, Δs, t1, t2, l, lп, q -? |
 Содержание
Содержание
Часть №1
Расчёт в предположении, что водяной пар – идеальный газ
1. Определение параметров в начальном состоянии…………………………………………4
1.1. Термические параметры………………………………………………………………..4
1.2. Калорические параметры……………………………………………………………….4
2. Определение параметров в конечном состоянии………………………………………….6
2.1. Термические параметры………………………………………………………………..6
2.2. Калорические параметры……………………………………………………………….6
3. Изменение калорических параметров в процессе…………………………………………8
3.1. Вычисление изменения калорических параметров по приближённым формулам…8
3.2. Вычисление изменения калорических параметров по уточнённым формулам…….8
4. Определение характеристик процесса…………………………………………………….10
5. Изображение процесса в  и
и  диаграммах……………………………………..11
диаграммах……………………………………..11
Часть №2
Расчёт в предположении, что водяной пар – реальный газ
1. Определение параметров в начальном и конечном состояниях с помощью таблиц водяного пара………………………………………………………………………………12
1.1. Определение параметров в начальном состоянии (в точке 1)……………………...12
1.2. Определение параметров в конечном состоянии (в точке 2)……………………….12
1.3. Изменение калорических параметров в процессе …………………………………..13
1.4. Характеристики процесса……………………………………………………………..13
2. Определение параметров в начальном и конечном состояниях по энтропийным диаграммам………………………………………………………………………………….14
2.1. Диаграмма  ……………………………………………………………………….14
……………………………………………………………………….14
2.2. Диаграмма  ……………………………………………………………………….15
……………………………………………………………………….15
2.3. Диаграмма  ……………………………………………………………………….16
……………………………………………………………………….16
3. Сопоставление параметров, найденных по таблицам и диаграммам…………………...17
4. Заключение………………………………………………………………………………….18
ЧАСТЬ №1
Расчёт в предположении, что водяной пар – идеальный газ
§ 1. Определение параметров в начальном состоянии (в точке 1)
1.1. Термические параметры (P1,T1, v 1)
По условию задачи в точке 1 заданы два независимых термических параметра: абсолютное давление (P1= 4бар =0,4МПа) и температура (t1=200°C –> T1=t1+273= 473 К).
Третий термический параметр – удельный объём – вычисляем из термического уравнения состояния идеального газа  :
:

В этом уравнении удельная (индивидуальная) газовая постоянная вычисляется по зависимости
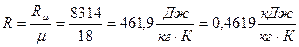 ,
,
где  – молярная (универсальная) газовая постоянная;
– молярная (универсальная) газовая постоянная;
 – молярная масса водяного пара.
– молярная масса водяного пара.
Масса водяного пара, участвующего в процессе:


1.2. Калорические параметры ( )
)
1.2.1 Случай 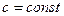 (по молекулярно-кинетической теории)
(по молекулярно-кинетической теории)
1) Из таблиц молярных теплоёмкостей, полученных на основе молекулярно-кинетической теории, для водяного пара ( ), как трёхатомного идеального газа, находим:
), как трёхатомного идеального газа, находим:
а) молярная изобарная теплоёмкость 
б) молярная изохорная теплоёмкость 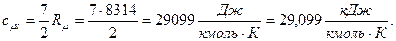
2) Удельные (массовые) теплоёмкости вычисляем по формулам пересчёта:
а) удельная изобарная теплоёмкость 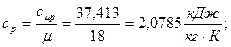
б) удельная изохорная теплоёмкость 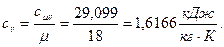
3) У  дельная энтальпия
дельная энтальпия
а)  начало отсчёта
начало отсчёта  ;
;
б)  начало отсчёта
начало отсчёта 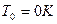 .
.
4)  Удельная внутренняя энергия
Удельная внутренняя энергия
а)  начало отсчёта
начало отсчёта  ;
;
б) 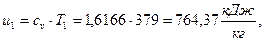 начало отсчёта
начало отсчёта 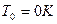 .
.
5) Удельная энтропия  начало отсчёта
начало отсчёта  ,
,  .
.
1.2.2. Случай  (по квантово-статистической теории).
(по квантово-статистической теории).
1. С помощью таблиц «Термодинамические свойства газов» (Ривкин С.Л.) для водяного пара ( ) как идеального газа при
) как идеального газа при  , находим:
, находим:
1) Удельная энтальпия  , начало отсчёта
, начало отсчёта 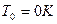 ;
;
2) Удельная внутренняя энергия 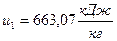 , начало отсчёта
, начало отсчёта 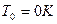 ;
;
3) Удельная энтропия рассчитывается по формуле  , где
, где  , начало отсчёта
, начало отсчёта 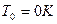 ,
,  .
.
2. С помощью таблиц средних теплоёмкостей для водяного пара ( ) как идеального газа при
) как идеального газа при  , находим:
, находим:
1) Средняя удельная изобарная теплоёмкость 
2) Средняя удельная изохорная теплоёмкость 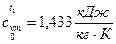 ;
;
3) Удельная энтальпия 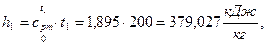 начало отсчёта
начало отсчёта  ;
;
4) Удельная внутренняя энергия  начало отсчёта
начало отсчёта  ;
;
5) Удельная энтропия с помощью средних теплоёмкостей точно не вычисляется.
 § 2. Определение параметров в конечном состоянии (в точке 2)
§ 2. Определение параметров в конечном состоянии (в точке 2)
2.1. Термические параметры ( )
)
По условию задачи в точке 2 заданы два независимых параметра:
термический - абсолютное давление ( ) и калорический – удельная энтропия(
) и калорический – удельная энтропия( ). Недостающие параметры – удельный объём и термодинамическая температура.
). Недостающие параметры – удельный объём и термодинамическая температура.
2.1.1 Случай, когда c=const:
Удельный объем находим из уравнения адиабатного процесса:  , где
, где  , из этого имеем:
, из этого имеем: 


Третий термический параметр – термодинамическая температура – вычисляем из термического уравнения состояния идеального газа 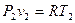 :
:

2.1.2 Случай, когда c=c(T)
1) Термодинамическую температуру определяем используя уравнение связи:  , где
, где  и
и  - функции температуры для данного ИГ.
- функции температуры для данного ИГ.
Из таблиц термодинамических свойств газов 
Отсюда имеем: 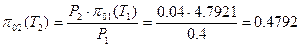
Из таблиц термодинамических свойств газов следует, что  при Т2=269 К
при Т2=269 К
2) Удельный объём определяем используя уравнение связи:
 , где
, где 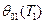 и
и  - функции температуры для данного ИГ.
- функции температуры для данного ИГ.
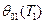 =
=
 =
=

Погрешность упрощенного расчета (c=const) по сравнению с уточненным (c=c(T)) равна:

2.2. Калорические параметры ( )
)
2.2.1 Случай 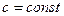 (по молекулярно-кинетической теории) при
(по молекулярно-кинетической теории) при 
1) Удельные (массовые) теплоёмкости вычисляем по формулам пересчёта:
а) удельная изобарная теплоёмкость 
б) удельная изохорная теплоёмкость 
2) Удельная энтальпия
а) 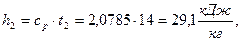 начало отсчёта
начало отсчёта  ;
;
б)  начало отсчёта
начало отсчёта 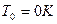 .
.
3)  Удельная внутренняя энергия
Удельная внутренняя энергия
а)  начало отсчёта
начало отсчёта  ;
;
б)  начало отсчёта
начало отсчёта 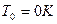 .
.
в) Удельная энтропия

Начало отсчета Т0=273К, Р0=0,1МПа.
2.2.2. Случай  (по квантово-статистической теории).
(по квантово-статистической теории).
1. С помощью таблиц «Термодинамические свойства газов» (Ривкин С.Л.) для водяного пара ( ) как идеального газа при
) как идеального газа при  , находим:
, находим:
1) Удельная энтальпия  , начало отсчёта
, начало отсчёта 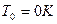 ;
;
2) Удельная внутренняя энергия 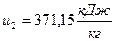 , начало отсчёта
, начало отсчёта 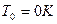 ;
;
3) Удельная энтропия рассчитывается по формуле  , где
, где  , начало отсчёта
, начало отсчёта 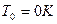 ,
,  .
.
2. С помощью таблиц средних теплоёмкостей для водяного пара ( ) как идеального газа при
) как идеального газа при  , мы не можем взять значения
, мы не можем взять значения  и
и  т.к. t2<0.
т.к. t2<0.
А значит и не можем вычислить h2, u2 и s2 …
§ 3. Изменение калорических параметров в процессе
3.1. Вычисление изменения калорических параметров по приближённым формулам (случай  )
)
1) Изменение удельной энтальпии  , начало отсчёта
, начало отсчёта  ;
;  , начало отсчёта
, начало отсчёта 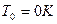 ; (Проверка:
; (Проверка: 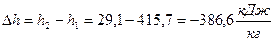 , начало отсчёта
, начало отсчёта  ;
;  , начало отсчёта
, начало отсчёта 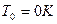 );
);
2) Изменение удельной внутренней энергии  , начало отсчёта
, начало отсчёта  ;
;  , начало отсчёта
, начало отсчёта 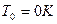 ; (Проверка:
; (Проверка:  , начало отсчёта
, начало отсчёта  ;
;  , начало отсчёта
, начало отсчёта 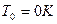 );
);
Из пунктов 1 и 2 мы видим, что изменение параметров не зависит от начала отсчёта и шкалы, по которой мы измеряем температуру (Цельсия или Кельвина).
3) Изменение удельной энтропии  , (Проверка:
, (Проверка: 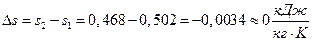 ).
).
Так как изменения калорических параметров вычисляются по приближённым формулам, то значения получены неточно.
В полных величинах:
 ;
;
 ;
;
 .
.
3.2. Вычисление изменения калорических параметров по уточнённым формулам (случай  )
) 
1. Пользуясь значениями, полученными из таблиц «Термодинамические свойства газов» (Ривкин С.Л.) для водяного пара ( ) как идеального газа, находим:
) как идеального газа, находим:
1) Изменение удельной энтальпии  ;
;
2) Изменение удельной внутренней энергии  ;
;
Изменение удельной энтропии  (Проверка:
(Проверка:  ).
).
В полных величинах:
1)  ;
;
2)  ;
;
3)  .
.
2. Пользуясь значениями, полученными из таблиц средних теплоёмкостей для водяного пара ( ) как идеального газа,
) как идеального газа,  мы не можем определить изменения калорических параметров т.к.
мы не можем определить изменения калорических параметров т.к. 
 § 4. Определение характеристик процесса (
§ 4. Определение характеристик процесса ( ,
,  ,
,  ,
, 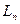 ,
,  ,
, 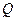 )
)
4.1. В процессе  тело не отдает и не получает теплоты из внешней среды:
тело не отдает и не получает теплоты из внешней среды:
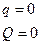
4.1.1. Случай 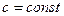 (по молекулярно-кинетической теории):
(по молекулярно-кинетической теории):
Для адиабатного процесса деформационная работа ( ) и работа перемещения (
) и работа перемещения ( ) связаны с понятием теплоемкости. Запишем эти зависимости:
) связаны с понятием теплоемкости. Запишем эти зависимости:
 кДж/кг
кДж/кг
 кДж/кг
кДж/кг
 кДж/кг
кДж/кг
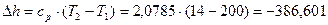 кДж/кг
кДж/кг
Выведем формулы для вычисления деформационной работы и работы перемещения:
1) Из уравнения энергобаланса для закрытых систем через деформационную работу в удельных величинах:
 ,
,  =>
=> 
 кДж/кг
кДж/кг
в полных величинах:
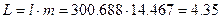 МДж
МДж
2) Из уравнения энергобаланса для закрытых систем через работу перемещения в удельных величинах:
 ,
,  =>
=> 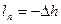
 кДж/кг
кДж/кг
в полных величинах
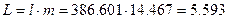 МДж
МДж
4.1.2. Случай  (по квантово-статистической теории):
(по квантово-статистической теории):
1)Из уравнения энергобаланса для закрытых систем через деформационную работу вычисляем по формуле:
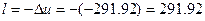 кДж/кг
кДж/кг
в полных величинах:
 МДж
МДж
2) Из уравнения энергобаланса для закрытых систем через работу перемещения в удельных величинах:
 , q=0 =>
, q=0 => 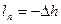
Удельную работу перемещения вычисляем по формуле:
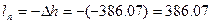 кДж/кг
кДж/кг
в полных величинах:


 МДж
МДж
Q=0 ΔU
Схема энергобаланса:
 Уменьшение внутренней энергии РТ
Уменьшение внутренней энергии РТ
идет на выполнение работы L
L
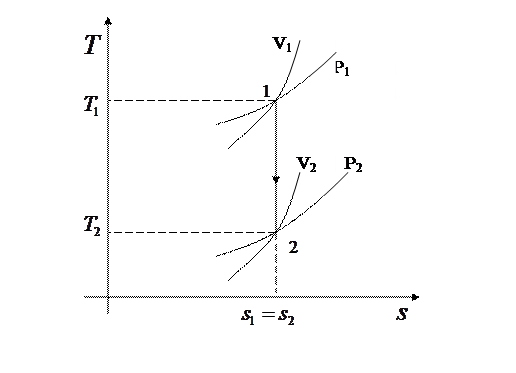
 § 5. Изображение процесса в
§ 5. Изображение процесса в  и
и  диаграммах
диаграммах
5.1.  диаграмма
диаграмма

5.2.  диаграмма
диаграмма

ЧАСТЬ №2
Расчёт в предположении, что водяной пар – реальный газ
§ 1. Определение параметров в начальном и конечном состояниях с помощью таблиц водяного пара
 1. Определение параметров в начальном состоянии (в точке 1)
1. Определение параметров в начальном состоянии (в точке 1)
По условию задачи в точке 1 заданы два независимых термических параметра: абсолютное давление (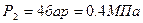 ) и удельный объём (
) и удельный объём ( ,
,  ). Эти данные позволяют найти все остальные.
). Эти данные позволяют найти все остальные.
С целью определения состояния реального газа по давлению  в таблице №2 находим температуру насыщения (
в таблице №2 находим температуру насыщения ( ). Так как t1>ts(P1), то данное состояние реального газа – перегретый пар. Его параметры находим по таблице №3:
). Так как t1>ts(P1), то данное состояние реального газа – перегретый пар. Его параметры находим по таблице №3:
– удельный объем 
– удельная энтальпия.  ;
;
– удельная энтропия.  ;
;
Удельную внутреннюю энергию рассчитываем по формуле:
 .
.
2. Определение параметров в конечном состоянии (в точке 2)
По условию задачи в точке 2 заданы два независимых параметра:
- термический: абсолютное давление ( )
)
- калорический: удельная энтропия (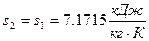 ), так как процесс адиабатный.
), так как процесс адиабатный.
Эти данные позволяют найти все остальные.
С целью определения состояния реального газа по давлению 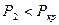 в таблице №2 находим:
в таблице №2 находим:
– удельную энтропию насыщенной жидкости  ;
;
– удельную энтропию сухого насыщенного пара  .
.
Так как при 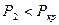
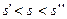 , то данное состояние реального газа – влажный насыщенный пар, следовательно
, то данное состояние реального газа – влажный насыщенный пар, следовательно 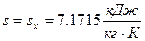 .
.
Параметры ВНП находим с помощью таблицы №2 и формул смешения.
Степень сухости  данного ВНП:
данного ВНП:
 .
.
Удельную энтальпию и удельный объём вычисляем по формулам смешения; значения необходимых параметров  ,
,  ,
,  ,
,  находим по давлению
находим по давлению 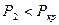 в таблице №2:
в таблице №2:
– удельная энтальпия:  ;
;
– удельный объём:  .
.
Удельную внутреннюю энергию рассчитываем по формуле:
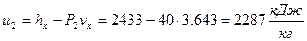 .
.
Температура ВНП в точке 2 равна температуре насыщения  .
.
 3. Изменение калорических параметров в процессе
3. Изменение калорических параметров в процессе
– изменение удельной энтальпии  ;
;
– изменение удельной энтропия  ;
;
– изменение удельной внутренней энергии  .
.
Масса водяного пара, участвующего в процессе:  .
.
В полных величинах:
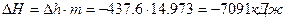 ;
;
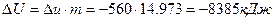 ;
;
 .
.
4. Характеристики процесса
4.1. Так как данный процесс изоэнтропный процесс ( ), тело не отдает и не получает теплоты из внешней среды: q=0, Q=0
), тело не отдает и не получает теплоты из внешней среды: q=0, Q=0
1) Из равнения энергобаланса для закрытых систем через деформационную работу в удельных величинах:  , в случае q =0 =>
, в случае q =0 => 
удельная деформационная работа
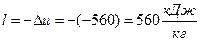
в полных величинах 
2) Из уравнения энергобаланса для закрытых систем через работу перемещения в удельных величинах:  , q =0 =>
, q =0 => 
|
|

 в полных величинах:
в полных величинах:

|

Уменьшение внутренней энергии РТ
идет на выполнение работы
§ 2. Определение параметров в начальном и конечном состояниях по энтропийным диаграммам
 2.1. Диаграмма
2.1. Диаграмма 
2.1.1. По условию задачи в точке 1 заданы два независимых термических параметра: абсолютное давление (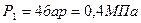 ) и температура (
) и температура ( ). Эти данные позволяют найти все остальные. С целью определения состояния реального газа по давлению
). Эти данные позволяют найти все остальные. С целью определения состояния реального газа по давлению  в t-s диаграмме находим температуру насыщения (
в t-s диаграмме находим температуру насыщения ( ). Так как
). Так как  , то состояние реального газа – перегретый пар. В области ПП на t-s диаграмме на пересечении P1 и t1 находим точку 1 и ее параметры:
, то состояние реального газа – перегретый пар. В области ПП на t-s диаграмме на пересечении P1 и t1 находим точку 1 и ее параметры:
– удельная энтальпия  ;
;
– удельная энтропия  .
.
– удельный объём 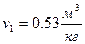 .
.
Удельную внутреннюю энергию рассчитываем по формуле:
 .
.
2.1.2. По условию задачи в точке 2 заданы два независимых параметра: термический – абсолютное давление (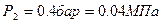 ) и калорический – удельная энтропия (
) и калорический – удельная энтропия ( ).Эти данные позволяют найти все остальные.
).Эти данные позволяют найти все остальные.
Температура ВНП в точке 2 равна температуре насыщения 
С целью определения состояния реального газа по давлению  в t-s диаграмме находим:
в t-s диаграмме находим:
- удельную энтропию насыщенной жидкости находим в точке пересечения Р2 и х= 0:
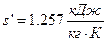
- удельную энтропию сухого насыщенного пара находим в точке пересечения Р2 и х= 1:

Так как  и
и  , то данное состояние реального газа – влажный насыщенный пар, следовательно
, то данное состояние реального газа – влажный насыщенный пар, следовательно 
В области ВНП на t-s диаграмме на пересечении изобары и изоэнтропы находим точку 2 и ее параметры:  .
.
– удельная энтальпия  ;
;
– удельный объём 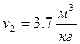 .
.
– удельная энтропия  ;
;
Удельную внутреннюю энергию рассчитываем по формуле:
 .
.
 Диаграмма
Диаграмма 
2.2. Диаграмма 
2.2.1. По условию задачи в точке 1 заданы два независимых термических параметра: абсолютное давление (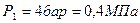 ) и температура (
) и температура ( ). Эти данные позволяют найти все остальные.
). Эти данные позволяют найти все остальные.
С целью определения состояния реального газа по давлению Р1<Pкр в h-s диаграмме находим температуру насыщения  . Так как
. Так как  , то данное состояние реального газа – перегретый пар. В области ПП на h-s диаграмме на пересечении Р1 и t1 находим точку 1 и ее параметры:
, то данное состояние реального газа – перегретый пар. В области ПП на h-s диаграмме на пересечении Р1 и t1 находим точку 1 и ее параметры:
– удельная энтальпия  ;
;
– удельная энтропия  .
.
– удельный объём  .
.
Удельную внутреннюю энергию рассчитываем по формуле:
 .
.
 |
2.2.2. По условию задачи в точке 2 заданы два независимых параметра: термический -абсолютное давление (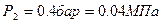 ) и калорический - удельная энтропия (
) и калорический - удельная энтропия (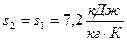 ).Эти данные позволяют найти все остальные.
).Эти данные позволяют найти все остальные.
С целью определения состояния реального газа по давлению Р2<Pкр в h-s диаграмме находим:
- удельную энтропию насыщенной жидкости:

- удельную энтропию сухого насыщенного пара находим в точке пересечения Р2 и х= 1:
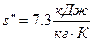
Так как  и
и  , то данное состояние реального газа – влажный насыщенный пар, следовательно
, то данное состояние реального газа – влажный насыщенный пар, следовательно 
Точка пересечения изобары и изоэнтропы находится в области ВНП. Её параметры:
Степень сухости  .
.
– удельная энтальпия  ;
;
– удельный объём  .
.
- удельная энтропия 
Удельную внутреннюю энергию рассчитываем по формуле:
 .
.
 Диаграмма
Диаграмма 




Диаграмма 

 |
§ 3. Сопоставление параметров, найденных по таблицам и диаграммам
 |
| Название величины, обозначение | Таблицы |  диаграмма диаграмма
|  диаграмма диаграмма
| |||
| точка 1 | точка 2 | точка 1 | точка 2 | точка 1 | точка 2 | |
Абсолютное давление 
| 0,4 | 0,04 | 0,4 | 0,04 | 0,4 | 0,04 |
Удельный объём 
| 0,5343 | 0,035 | 0,53 | 3.7 | 0,56 | 3.9 |
Термодинамическая температура 
| 75,89 | |||||
Удельная энтальпия 
| 2860,6 | 54,33 | ||||
Удельная энтропия 
| 7,1715 | 7,1715 | 7,165 | 7,165 | 7,2 | 7.2 |
Удельная внутренняя энергия 
|
 Заключение
Заключение
В данной расчётно-графической работе были определены все начальные и конечные параметры рабочего тела, их изменение и характеристики процесса. Процесс адиабатный (изоэнтропный), поэтому теплота  . Результаты расчёта показывают, что в данном адиабатном процессе с уменьшением давления температура водяного пара понижается. При этом энтальпия, энтропия и внутренняя энергия уменьшаются, а энтропия остается постоянной:
. Результаты расчёта показывают, что в данном адиабатном процессе с уменьшением давления температура водяного пара понижается. При этом энтальпия, энтропия и внутренняя энергия уменьшаются, а энтропия остается постоянной: 
Расчёт был произведён для двух случаев:
1 В предположении, что водяной пар – идеальный газ. В этом случае параметры и характеристики процесса определялись для двух вариантов:
1) 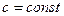 : при нахождении изменения калорических параметров был сделан вывод, что изменение параметров не зависит от начала отсчета при измерении температуры.
: при нахождении изменения калорических параметров был сделан вывод, что изменение параметров не зависит от начала отсчета при измерении температуры.
2)  : калорические параметры были определены с помощью таблиц «Термодинамические свойства газов» Ривкина С.Л. и таблиц средних теплоемкостей, причем энтропия через средние теплоемкости не вычисляется.
: калорические параметры были определены с помощью таблиц «Термодинамические свойства газов» Ривкина С.Л. и таблиц средних теплоемкостей, причем энтропия через средние теплоемкости не вычисляется.
Для идеального газа приведены изображения процесса в 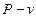 и
и  диаграммах.
диаграммах.
2 В предположении, что водяной пар – реальный газ. В этом случае параметры и характеристики процесса определялись с помощью:
1) таблиц водяного пара;
2) масштабных диаграмм.
Для реального газа приведены изображения процесса в  ,
,  и
и  диаграммах.
диаграммах.
3 Сравним характеристики процессов в 1 и 2 части работы:
1) деформационная работа: погрешность расчетов для РГ и ИГ (с=с(Т))
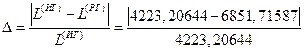
В конце работы приведено сопоставление параметров реального газа, найденных по таблицам и диаграммам, с помощью которого можно судить о правильности выполнения работы.
Таким образом, было определено, что уменьшение внутренней энергии РТ идет на выполнение работы.
Литература:
1. Ривкин С.Л. «Термодинамика, свойства идеальных газов».
2. Ривкин С.Л., Александров А.А. «Термодинамика, свойства воды и водяного пара».






