Ряд. Виды рядов
Рядом называют сумму членов бесконечной последовательности
.
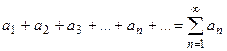Слагаемые в этой сумме называют членами ряда, член с произвольным номером 
– общим членом ряда.
Если члены ряда числа, ряд называют числовым. Если членами ряда являются функции, его называют функциональным.
Среди функциональных рядов наиболее широко используют степенной ряд:
и тригонометрический ряд:
С первоначальными понятиями теории рядов связаны два следующих типа задач:
Пример 1. По данной формуле общего члена 
записать его несколько первых членов*.
Решение. Для вычисления любого члена ряда нужно в формулу общего члена вместо n подставить номер этого члена. Поэтому 
; 
и так далее.
Ответ: 
Пример 2. Запишите формулу общего члена ряда по нескольким его первым членам: 
Решение. Если ряд знакочередующийся, формула общего члена должна содержать множитель 
или 
для ряда, у которого первый член положителен, и множитель 
для ряда с первым отрицательным членом.
Далее нужно попытаться установить закономерность в записи членов ряда в зависимости от их номера. В данном примере члены ряда – дроби. Проследим за изменением числителя. У первого члена он равен 2, у второго – 4, у третьего – 8, у четвертого – 16 и у пятого –32. Можно заметить, что числители – это степени числа 2 с показателем, равным номеру члена. То есть член с произвольным номером n будет содержать в числителе 
.
Теперь проследим за значениями знаменателей. У первой дроби он равен 1, у второй – 4, у третей – 9, у четвертой – 16 и у пятой – 25. То есть, знаменатель равен квадрату номера члена. Для члена с произвольным номером n он равен 
.
Из проведенных рассуждений следует
Ответ: 
.
Сходимость ряда
Рассмотрим ряд 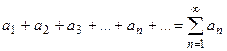. Построим его частичные суммы:
Ряд называют сходящимся, если бесконечная последовательность его частичных сумм имеет конечный предел: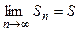 
. Этот предел называется суммой сходящегося ряда. Если 
не существует или бесконечен, ряд называют расходящимся.
Когда рассматривают функциональный ряд, он может обратиться в сходящийся или расходящийся числовой ряд в зависимости от значения входящей в него переменной. Множество значений переменной, при которых функциональный ряд превращается в сходящийся числовой ряд, называют интервалом сходимости функционального ряда.
Теорема 1 (необходимый признак сходимости ряда). Если ряд сходится, его члены стремятся к нулю.
Доказательство. Пусть ряд 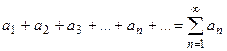сходится. По определению это означает, что .
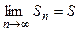Выпишем две частичные суммы ряда:
Вычитая из второй строки первую, получим 
. Рассмотрим
,
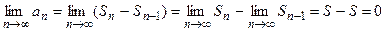что и требовалось доказать.
Доказанный признак является необходимым. То есть он выполняется для сходящегося ряда. Поэтому пользоваться им для исследования ряда на сходимость нельзя. Но из него следует: если 
, то ряд расходится – это достаточный признак расходимости ряда.
Пример. Докажите расходимость ряда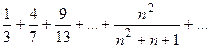 
Решение. Рассмотрим
.
Так как 
, то ряд расходится.
Основные теоремы о сходящихся рядах
Теорема 1:
Если ряд 
- сходится, то сходится ряд:
Получаемый из данного ряда отбрасыванием n первых членов; наоборот, из сходимости n-го остатка ряда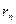 
вытекает сходимость данного ряда
Теорема 2:
Если сходится ряд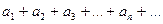 
(1)
и суммой его является число S, то сходится и ряд 
(2)
причем сумма ряда (2) равна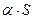 
Теорема 3:
Если сходится ряд
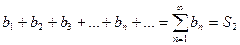
То сходится и ряд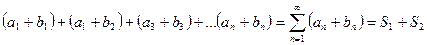 
Признак сходимости.
I признак
Пусть даны два ряда с положительными членами:
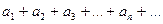(1)
(2)
Тогда:
1) если сходится ряд (2), то сходится ряд (1)
2) если расходится ряд (1), то расходится и ряд (2)
II признак
Если конечный, отличный от нуля предел
, то оба ряда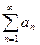 
и 
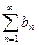
одновременно сходятся и одновременно расходятся
Признак Коши
Если для ряда
, 
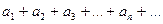существует 
, то этот ряд сходится при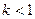 
и расходится при 
Признак Даламбера
Теорема. Пусть для ряда 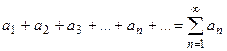существует 
. В таком случае:
1) если предел l < 1, то ряд сходится;
2) если l > 1, то ряд расходится;
3) если l = 1, то признак определенного ответа не дает, так как в этом случае одни рады сходятся, а другие расходятся.
Признаком Даламбера можно пользоваться для исследования ряда на сходимость и нахождения интервала сходимости ряда. Для этого удобно пользоваться следующим алгоритмом:
1. Записать общий член ряда .
2. Записать последующий член 
, для чего в формулу общего члена везде подставить n + 1 вместо n.
3. Вычислить дробь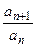 
.
4. Вычислить предел модуля полученной дроби при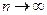 
.
5. Если ряд числовой, по значению предела сделать заключение о сходимости этого ряда. В противном случае перейти к пункту 6.
6. Записать неравенство: значение предела < 1.
7. Решить полученное неравенство. Его решение и есть интервал сходимости с точностью до ответа на вопрос, входят ли в него граничные точки (этот вопрос требует дополнительных исследований).
Пример 1. Исследуйте по признаку Даламбера сходимость ряда
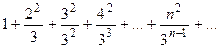
Решение. Общий член ряда задан 
.
Запишем последующий член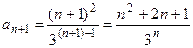 
.
Вычислим дробь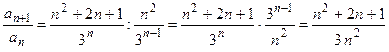 
.
Вычислим предел модуля этой дроби
.
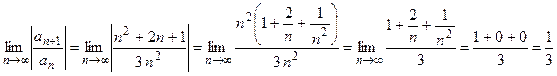Так как вычисленный предел равен 
, то ряд сходится.
Пример 2. Найдите промежуток сходимости ряда 
По виду членов ряда запишем его общий член 
.
Тогда последующий член имеет вид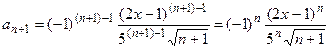 
.
Вычислим дробь 
.
Вычислим предел модуля полученной дроби
.
Ряд сходится для тех значений аргумента, для которых 
.
Решим это неравенство, для чего заменим его двойным неравенством без модуля
.
Умножим все части неравенства на 5: 
.
Прибавим ко всем частям 1: 
.
Разделим все части неравенства на 2: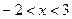 
.
Ответ: интервал сходимости ряда (– 2; 3).
Признак Лейбница
Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю, т.е. если выполняется следующие 2 условия:
1) 
2) 
Сумма знакочередующегося ряда меньше первого члена ряда, т.е. 
Определение. Знакопеременные ряды – это ряды с произвольным чередованием знаков его членов.
Теорема. Знакопеременный ряд
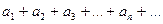- сходится, если ряд
Определение. Сходящийся ряд 
называется абсолютно сходящимся, если ряд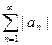 
- сходится и условно сходится, если ряд 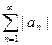- расходится.
* В математике записью n! принято обозначать произведение первых n натуральных чисел. Например, 3!=1×2×3=6; 6!=1×2×3×4×5×6=720.
