При описании математической модели магнитотеллурического поля пользуются низкочастотным, квазистационарным приближением. Но начать следует с рассмотрения полной модели, учитывающей токи смещения. В среде с параметрами ε, μ и σ электромагнитное поле описывается уравнениями Максвелла в следующем виде
(3.1) 
(3.2)
(3.3) 
(3.4).
Электромагнитное поле в реальных средах и уравнения связ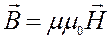и 
и 
удовлетворяют закону Ома в дифференциальной форме 
(3.5) и уравнению непрерывности, вытекающему из 1 и уравнений Максвелла
(3.6)
Здесь 
- относительная магнитная проницаемость среды (безразмерная величина), 
- абсолютная магнитная постоянная вакуума, 
- относительная диэлектрическая проницаемость среды - безразмерная величина, изменяющаяся в реальных геологических средах от 1 до 80, 
- абсолютная диэлектрическая постоянная вакуума;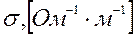 
- удельная электропроводность среды, 
- плотность тока.
Рассмотрим уравнения Максвелла в условиях однородной изотропной среды. Кроме того, будем считать, что электромагнитное поле устанавливается сразу после включения источника. Это означает, что в однородной проводящей среде, за пределами источника свободные заряды не накапливаются, то есть плотность свободных зарядов равна нулю и существуют только силовые линии поля, втекающие и вытекающие через любое замкнутое пространство. Тогда четвертое уравнение Максвелла (3.4) при 
может быть записано в следующем виде
. (3.7)
Однако этот тезис требует доказательства. Для этого возьмем дивергенцию от правой и левой частей первого уравнения Максвелла (3.1).
. (3.8)
Члены правой части уравнения (3.8), с учетом четвертого уравнения Максвелла (3.4) и закона Ома в дифференциальной форме (3.5), могут быть приведены к виду.
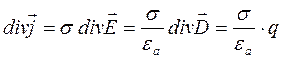, (3.9)
. (3.10)
Поскольку 
, то уравнение (3.8), приобретает вид дифференциального уравнения для объемной плотности заряда q
(3.11)
Уравнение (3.10) имеет своим решением выражение для плотности зарядов определяемое экспоненциальной зависимостью вида
, (3.12)
где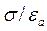 
- постоянная релаксации свободных электрических зарядов; 
– объемная плотность свободных зарядов в исследуемом пространстве в момент возникновения поля при t = 0. В реальных геологических средах средняя удельная электропроводность принята равной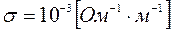 
; относительная диэлектрическая проницаемость в подавляющем большинстве геологических сред 
и, следовательно, абсолютная диэлектрическая проницаемость 
, а постоянная релаксации свободных зарядов 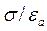= 108 [с-1]. Отсюда уравнение (3.12) примет вид 
. Это означает, что уже на самых ранних временах, через 10-7 с после отключения источника, плотность свободных зарядов составляет q=qo·e -10, то есть уменьшается более чем в 1000 раз относительно первоначальной величины. Это позволяет считать, что в области однородности, то есть вдали от источника и на не очень коротких временах 
четвертое уравнение Максвелла (3.4) имеет вид divE=0.
С учетом приведенных выше условий однородности (условий отсутствия свободных зарядов), а также считая, что в изучаемом пространстве отсутствуют сторонние э.д.с. (двойные электрические слои, поля электрохимической природы и др.) и принимая 
, уравнения Максвелла приобретают вид:
(3.12)
Заложенная в уравнениях Максвелла внутренняя связь электрических и магнитных полей позволяет разделить их, т.е. записать отдельно уравнения для векторов 
и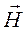 
. Для этого подействуем на левые и правые части первого уравнения системы уравнений (3.12) оператором 
.
. (3.13)
Учитывая, что 
, а также учитывая, что 
и 
(лапласиан), уравнение (3.13) после подстановки в него значения 
из второго уравнения системы (3.12), принимает вид:
, (3.14)
После преобразования второго уравнения Максвелла из системы (3.12) нетрудно получить аналогичного вида запись для поля 
:
(3.15)
Уравнения (3.14) и (3.15) получили название телеграфных. В них участвуют два слагаемых с коэффициентами 
и 
. Они могут быть представлены в следующем виде:
, (3.16)
, (3.17)
Здесь М – коэффициент диффузии электромагнитного поля и с – скорость света. Из уравнений (3.14) и (3.15) можно видеть, что в распространении электромагнитного поля участвуют два процесса – диффузионный, определяемый коэффициентом диффузии поля М (3.16) и волновой, определяемый скоростью света с (3.17). Волна распространяется в верхнем полупространстве со скоростью света 
. За этой волной тянется диффузионный шлейф, состоящий из токов и магнитных силовых линий, индуцированных в проводящей среде. Длительность распада электромагнитного поля в земле (диффузии) может быть оценена по приближенной формуле:
(3.18).
где L2 – площадь участка земной поверхности с поперечным размером L, по которому пробежала электромагнитная волна.
Например, территорию с поперечным сечением L=300 км электромагнитная волна пересечет за 10-3 с, а диффузия (при ρ=103 Ом·м) длится примерно 100 с (т.е. скорее установленных нами 3 км/с). В этих условиях можно считать, что волна распространяется мгновенно, и мы можем наблюдать только распад индуцированных в земле токов, то есть диффузию, подобную теплу от нагретого тела. Описанный пример иллюстрирует основной принцип разделения электромагнитного поля в электроразведке на волновую, квазистационарную и стационарную модели. В этой ситуации можно считать, что электромагнитная волна пробегает данную область мгновенно и в реальном времени можно наблюдать только результат ее действия – т.е. диффузию. Это равносильно исключению из (3.14) и (3.15) второй производной по времени и рассмотрению уравнений Максвелла в приближенном (квазистационарном) виде. Отсюда уравнения (3.14) и (3.15) принимают вид диффузионных уравнений, называемых еще уравнениями теплопроводности:
(3.19)
Им соответствуют уравнения Максвелла в квазистационарном приближении:
(3.20)
Это означает, что электромагнитное поле имеет волновую природу только в верхнем полупространстве, в условиях вакуума, имеющего бесконечно высокое сопротивление. В нижнем полупространстве, в проводящей среде электромагнитное поле распространяется подобно теплу, по законам диффузии. В случае гармонического поля, изменяющегося по закону 
, уравнения (3.20) принимают вид
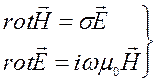(3.21)
