Содержание
1. Задание на курсовой проект и данные по варианту.
2. Системы уравнений в нормальной форме Коши. Разностная схема для решения системы уравнений подводного аппарата и следящей системы методом Эйлера.
3. Описание и инструкция по использованию программы.
4. Оптимизация параметров регулятора следящей системы.
5. Графики.
Задание и структурная схема исследуемой системы управления
Построить систему управления подводным аппаратом по курсу и по глубине, воздействуя на горизонтальные рули Dg и вертикальные рули Db (максимальное отклонение рулей ± 0.5 радиан).
Структура системы, подлежащей исследованию, представлена на рис.1.
Рис. 1. Структура системы управления
Основные обозначения координат и углов приведены на рис.2. Управляющими воздействиями являются отклонения горизонтальных и вертикальных кормовых рулей Dg, Db. Необходимо управлять глубиной погружения Eta и курсом Fi подводного аппарата.
 |
Рис. 2. Основные координаты подводного аппарата
Структурная схема следящей системы исполнительного механизма представлена на рис.3. Структурные схемы для следящих систем исполнительных механизмов вертикальных и горизонтальных рулей считать одинаковыми.
 |
Рис.3. Структурная схема следящей системы исполнительного механизма.
Данные по варианту:
| № студента в списке | ||
| Блоки исполнительного механизма | блок 1 | Интег-ратор, охваченный обратной связью |
| блок 2 | Составной блок | |
| Коэф- фициенты блока 1 | К1 | |
| Т1 | 0.4 | |
| Ksi1 | - | |
| Коэф- фициенты блока 2 | К2 | |
| Т2 | 0.5 | |
| Ksi2 | - | |
| Тип регулятора | ПИД | |
| Исходные параметры регулятора | Кп | 0.5 |
| Ки | 0.8 | |
| Lи | 3.5 | |
| Кд | 0.4 | |
| Тд | 0.1 | |
| Критерий | J1 | |
| Весовые коэф-ты | r1 | 0.9 |
| r2 | 0.1 | |
| Оптимизируемые параметры | Кп | |
| Ки |
| Интегратор, охваченный обратной связью |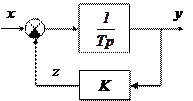 
| 
| ||
Составной блок
| 
| |||
 Пропорционально-интегрально-дифференциальный
(ПИД-регулятор)
|
| u=u1 + u2 + u3 Выходной сигнал интегратора ограничен величиной LИ. Используется реальное дифференцирующее звено. |
Системы уравнений в нормальной форме Коши. Разностная схема для решения системы уравнений подводного аппарата и следящей системы методом Эйлера
Модель интегратора, охваченного обратной связью:
Передаточные функции блока:
,
т.е.
Дифференциальное уравнение:
Переход к разностным уравнениям по методу Эйлера (h – шаг расчета):
h=DynTime-t0;
y=y+h*(x-z)/T;
z=K*y;
t0=DynTime;
Модель составного блока:
Передаточные функции блоков:
т.е.
Дифференциальные уравнения:
или
Переход к разностным уравнениям по методу Эйлера (h – шаг расчета):
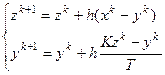
h=DynTime-t0;
z=z+h*(x-y);
y=y+h*(K*z-y)/T;
t0=DynTime;
Модель ПИД-регулятора:
Передаточные функции блоков:
u=u1 + u2 + u3
Переход к разностным уравнениям по методу Эйлера (h – шаг расчета):
h=DynTime-t0;
u1=Kp*e;
u2=u2+h*(Ki*e);
if (u2>Li) u2=Li; else if (u2<-Li) u2=-Li;
zn=z+h*(e-z)/Td;
u3=Kd*(e-z)/Td;
u=u1+u2+u3;
t0=DynTime;
Модель подводного аппарата:
Дифференциальные уравнения:
В уравнениях 2,4 и 6 в правой части присутствуют производные. Подставим в уравнение 6 вместо dVy/dt правую часть уравнения 2, а вместо dVz/dt правую часть уравнения 3. Предварительно, чтобы не писать каждый раз большое число слагаемых, обозначим:
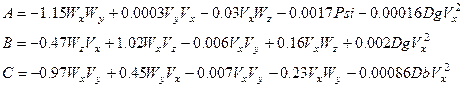
С этими подстановками и решая уравнения относительно dWz/dt, получаем:
Подставив вместо dVz/dt переменную С получим:
Переходим к разностным уравнениям по методу Эйлера:
где
