Многофакторный корреляционно-регрессионный анализ

Отчеты

По лабораторным работам

по дисциплине «Статистика»

Вариант №5

 

Выполнил: студент 2-го курса

Группы ПИЭ – 208 Кочетков А.Д.

Проверил: преподаватель

Будник Е.Е.

 

 

Лабораторная работа №1

Задание 1

В течении нескольких сотен часов регистрировалось число посетителей популярного сайта. Используя систему Statistica, определите абсолютные и относительные показатели вариации. Определите, какому закону распределения подчиняются эти данные.

 

 

Кол-во посетителей, чел.	Кол-во часов

 

Задание 2

Имеются данные о росте сотрудников подразделения. В соответствии с вашим вариантом определите:

1) средние величины: средний рост сотрудников в подразделении, моду и медиану;

2) абсолютные показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение.

3) относительные показатели вариации: коэффициенты осцилляции, вариации и линейной вариации; Сделайте вывод по однородности совокупности.

4) коэффициент асимметрии, эксцесса, сделать вывод о симметричности.

5) оформить отчет.

 

Номер варианта
Рост сотрудников (м)	Количество сотрудников (чел.)
1,52–1,60
1,60—1,68
1,68—1,76
1,76—1,84
1,84—1,92
1,92—2,0

 

Номер варианта
Рост сотрудников (м)	Количество сотрудников (чел.)
1,52–1,60
1,60—1,68
1,68—1,76
1,76—1,84
1,84—1,92
1,92—2,0

 

Глоссарий

 

Valid N – число наблюдений N

Mean - среднее

Sum - сумма

Median - медиана

Standard deviation – стандартное отклонение

Variance- дисперсия

Standard error of mean – стандартная ошибка среднего

Confidence limits of mean - доверительные границы для среднего

Minimum Maximum – минимум и максимум

Range - размах

Skewness - асимметрия

Kurtosis - эксцесс

Standard error of Skewness – стандартная ошибка асимметрии

Standard error of Kurtosis – стандартная ошибка эксцесса

 

Задание 1.

Найдем показатели вариации выбрав описательные статистики и указав нужные параметры:

 

 

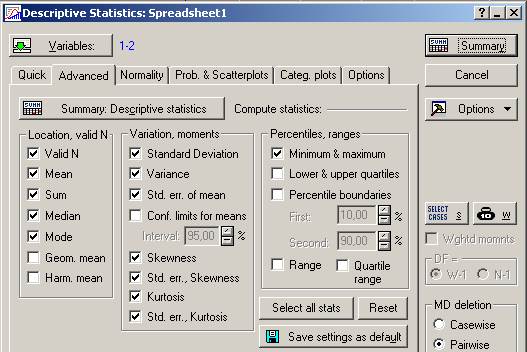
Результат:

 

 

Задание 2.

Найдем нужные показатели:

 

 

Результаты:

 

 

 

 

 

Лабораторная работа №2

Задание

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость выпуска объема продукции (Y, млн руб) от объема капиталовложений (X млн руб). (табл. 6)

Требуется:

1. Для характеристики Y от X построить следующие модели:

- линейную,

- степенную,

- показательную,

- гиперболическую.

2. Оценить каждую модель, определив:

- индекс корреляции,

- среднюю относительную ошибку,

- коэффициент детерминации,

- F – критерий Фишера.

3. Составить свободную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.

4. Рассчитать прогнозные значения результативного признака на 110% относительно среднего уровня.

Таблица 6

Вариант	Наблюдения
	Y
X
	Y
X
	Y
X
	Y
X
	Y
X
	Y
X
	Y
X
	Y
X
	Y
X
	Y

 

Линейная модель

 

Степенная модель

Показательная модель

Гиперболическая модель

 

 

Наибольшее значение F-критерия Фишера и большее значение коэффициента детерминации R² имеет линейная модель. Ее можно взять в качестве лучшей для построения прогноза.

Расчет прогнозного значения результативного показателя для Уральского региона:

X_ПР=X*1,1=42,86*1,1=47,146; Упр=44,65+0,76*X

Лабораторная работа № 3

 

Задание. В базе данных (файл – Lab2.sta) даны значения показателей производственно-хозяйственной деятельности промышленных предприятий.

 

Рассматриваются следующие показатели:

Y₁ – производительность труда

Y₂ – индекс снижения себестоимости продукции

Y₃ – рентабельность

Х₄ – трудоемкость единицы продукции

Х₅ – удельный вес рабочих в составе ППП

Х₆ – удельный вес покупных изделий

Х₇ – коэффициент сменности оборудования

Х₈ – премии и вознаграждения на одного работника

Х₉ – удельный вес потерь от брака

Х₁₀ – фондоотдача

Х₁₁ – среднегодовая численность ППП

Х₁₂ – среднегодовая стоимость ОПФ

Х₁₃ – среднегодовой фонд заработной платы ППП

Х₁₄ – фондовооруженность труда

Х₁₅ – оборачиваемость нормируемых оборотных средств

Х₁₆ – оборачиваемость ненормируемых оборотных средств

Х₁₇ – непроизводственные расходы.

 

НЕОБХОДИМО:

 

1) Построить однофакторную модель зависимости результативного признака Y от факторного признака Х в соответствии с вариантами заданий.

Установить вид аппроксимирующей функции. Определить силу и направление связи между переменными. Определить какая часть вариации результативного признака объясняется влиянием факторного признака. Построить уравнение регрессии. Оценить адекватность модели. Проанализировать остатки. Спрогнозировать значение результативной переменной при указанном значении факторной переменной.

 

2) Построить многофакторную модель зависимости результативного признака Y от факторных признаков Х в соответствии с вариантами заданий.

Установить вид аппроксимирующей функции. Определить силу и направление связи между результативной переменной и каждой факторной переменной и, в общем, между результативной переменной и всеми значимыми факторными переменными. Определить тесноту связи между результативным признаком и каждым из факторных признаков при исключении влияния других признаков. Определить какая часть вариации результативного признака объясняется влиянием факторных признаков. Построить уравнение регрессии. Оценить адекватность модели. Проанализировать остатки. Спрогнозировать значение результативной переменной при указанном значении факторных переменных.

Варианты заданий

№ варианта	Однофакторная модель	Многофакторная модель
Результативный признак, Y	Номер факторного признака, Х	Результативный признак, Y	Номера факторных признаков, Х
				6, 8, 11, 12, 17
				7, 11, 12, 13, 17
				8, 11, 12, 13, 17
				5, 6, 12, 13, 17
				5, 6, 7, 9, 17
				8, 9, 13, 14, 17
				6, 8, 13, 14, 17

 

Х4	Х5	Х6	Х7	Х8	Х9	Х10	Х11	Х12	Х13	Х14	Х15	Х16	Х17
0,31	0,74	0,22	1,22	2,2	0,79	1,39		78,11		6,62	120,52	14,76	19,41

Значения факторных переменных, для прогноза результативного признака:

 

Выполнение работы

1) Построим однофакторную регрессионную модель для анализа влияния вариации факторного признака X8 на результативный признак Y3.

 

Рис. «Поле корреляции и гистограммы переменных»
Х₈ и У₁ .

 

 

Для удаления выбросов используют средство Brushing – Кисть, меню которого активизируется кнопкой на панели инструментов.

В группе опций Action – Действия установим маркер на действие Label и, подведя курсор-лупу к предполагаемому «выбросу» на графике поля корреляции, щелкнем левой кнопкой мыши. Соответствующая точка-«выброс» будет выделена. Далее нажмем кнопку Update-Обновить для определения порядкового номера случая-«выброса». Над точкой появился номер: Case 4- Наблюдение 4. Для удаления «выброса» с графика поля корреляции установим маркер на действие Turn OFF - Отключить и нажмем Update-Обновить. Аналогичным образом удалим оставшиеся выбросы. Направление аппроксимирующей функции изменилось, теперь все точки лежат в непосредственной ее близости. Можно сделать вывод о сильном влиянии выброса на результат анализа, удалить выбросы из исходных данных и заново рассчитать коэффициент парной корреляции.

Нажатием кнопки Quit – Выход закончим использование инструмента Brushing – Кисть. Удалим выброс и из исходных данных, предварительно закрыв диалоговое окно Review Descriptive statistics – Просмотр описательных статистических характеристик. Далее снова вызовем Startup Panel – Стартовую панель в меню Analysis-Анализ и проведем расчет коэффициента парной корреляции.

 

 

 

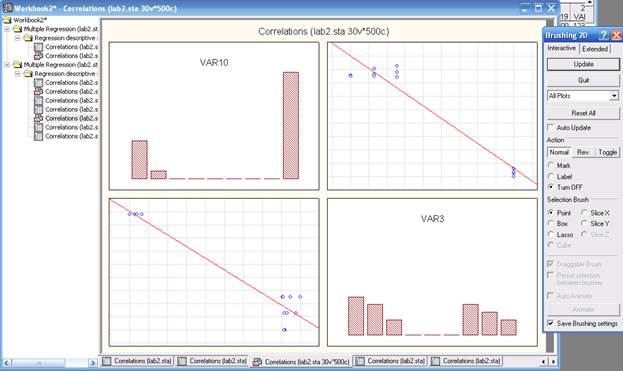
Рис. «Использование инструмента Brushing – Кисть»

 

Заново рассчитанный коэффициент парной корреляции равен 0,25, что свидетельствует о возможном наличии прямой связи между рассматриваемыми переменными. Принимая гипотезу о прямолинейной форме зависимости между признаками, определим значения параметров b₀ и b₁ уравнения однофакторной линейной корреляционной связи вида ŷ=b₀+b₁x.

Из диалогового окна Review Descriptive statistics – Просмотр описательных статистических характеристик, щелчком на кнопке ОК переходим в диалоговое окно Model Definition – Определение модели, а из него щелчком на кнопке ОК – в окно результатов корреляционно-регрессионного анализа.

По данным нашего примера коэффициент детерминации получился равным 0,06242348, таким образом, 6,2% вариации показателя Х₈ объясняется вариацией показателя .

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=18 (20 наблюдений минус 2 равно 18) при уровне значимости α=0,05 равно 4,41, а рассчитанное значение равно 1,198433. Расчетное значение меньше табличного, поэтому найденный коэффициента парной корреляции имеет малую значимость между переменными Х₈ и . Как правило F_расч > F_табл минимум в 4 раза.

 

Рис. «Окно результатов корреляционно-регрессионного анализа»

 

Щелчок по кнопке Regression Summary –Итоговая таблица регрессии в окне результатов регрессионного анализа открывает Regression Summary for dependent variable – Итоговую таблицу регрессии зависимой переменной.

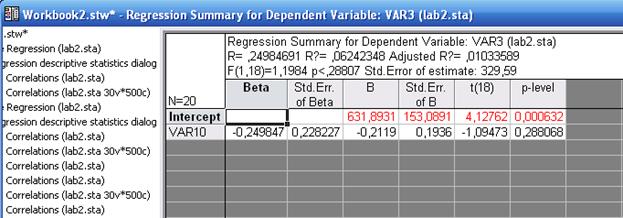
Рис. «Окно Regression Summary for dependent variable –
Итоговая таблица регрессии зависимой переменной»

Здесь в столбце B отражены искомые значения параметров b₀ и b₁ регрессионного уравнения. Итак, наше уравнение имеет вид:

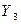=631,8931-0,2119* Х₈

Значимость найденных параметров b₀ и b₁ проверяется по таблице t-критерия Стьюдента. Расчетные значения t-критерия Стьюдента для каждого параметра, отраженные в столбце t(18), сравниваем с табличным значением t-критерия для числа степеней свобода, равного 18. t_табл = 2,101 при уровне значимости α=0,05. Рассчитанные значения t-критерия для первого параметра больше табличного, для второго – меньше.

 

 

Многофакторный корреляционно-регрессионный анализ

Включим в модель переменные Х₅ Х₆ Х₇ Х₉ Х₁₇. Построим многофакторную линейную регрессионную модель для анализа влияния вариации факторных признаков Х₅ Х₆ Х₇ Х₉ Х₁₇ на результативный признак .

Выявление и удаление выбросов проводятся аналогично описанному процессу для случая однофакторной регрессии.

Рис. «Поле корреляции и гистограммы переменных , Х₅ Х₆ Х₇ Х₉ Х₁₇»

Корреляционная матрица содержит коэффициенты корреляции как между факторными и результирующей переменной, так и между самими факторными переменными.

Рис. «Корреляционная матрица»

 

Корреляционная матрица показывает, что значение коэффициента парной корреляции между переменными и равно -0,419, т.е. направление связи – обратное, связь слабая.

Х₅ и =-0,434259, направление связи – обратное, связь слабая.

Х₆и =-0,042073, направление связи – обратное, связь слабая.

Х₇и =-0,132478, направление связи – обратное, связь слабая.

Х₉и =0,164505, направление связи – обратное, связь слабая.

 

В случае построения многофакторной модели требуется проверить факторы на мультиколлинеарность. В нашем примере коэффициент корреляции между факторами (равный -0,434259) меньше коэффициентов корреляции факторов с результирующей переменной (соответственно -0,042073 и 0,031845), т.е. мультиколлинеарность отсутствует.

Определим значения параметров b₀, b₁ , b_2, b₃, b₄ , b_5, уравнения многофакторной линейной корреляционной связи вида ŷ=b₀+b₁x+ b₂x+ b₃x+ b₄x+ b₅x.

 

Рис. «Окно Regression Summary for dependent variable – Итоговая таблица регрессии зависимой переменной»

В нашем примере b₀ = -47,8959 b₁ = 0,0337, b₂ = 1,0036,

b₃ = 0,0420, b₄ = -0,1378, b₅ = 7,0899, уравнение регрессии имеет вид:

=-47,8959 +0,0337 Х₅+1,0036 Х₆+0,0420 Х₇-0,1378 Х₉+7,0899 Х₁₇

Совокупный коэффициент множественной детерминации, равный 0,99920129, показывает, что 99,9% вариации показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии (Х₅ Х₆ Х₇ Х₉ Х₁₇).

Проверка адекватности уравнения, значимости найденных коэффициентов регрессии, построение прогноза осуществляются так же, как при проведении однофакторного корреляционно-регрессионного анализа.

 

Рис. «Окно результатов корреляционно-регрессионного анализа»

 

Значимость множественного коэффициента корреляции проверяется по таблице F-критерия Фишера. В нашем случае табличное значение F-критерия Фишера для степеней свободы ν₁=1, ν₂=18 (20 наблюдений минус 2 равно 18) при уровне значимости α=0,05 равно 4,41, а рассчитанное значение равно 4754,852. Расчетное значение больше табличного, поэтому найденный коэффициент парной корреляции имеет высокую значимость между переменными , Х₅ Х₆ Х₇ Х₉ Х₁₇. Как правило F_расч > F_табл минимум в 4 раза.

 

Нажатие по кнопке Graph – График в диалоговом окне Review Descriptive statistics – Просмотр описательных статистических характеристик откроет график «поле корреляции» исследуемых переменных, а также соответствующие гистограммы.

 

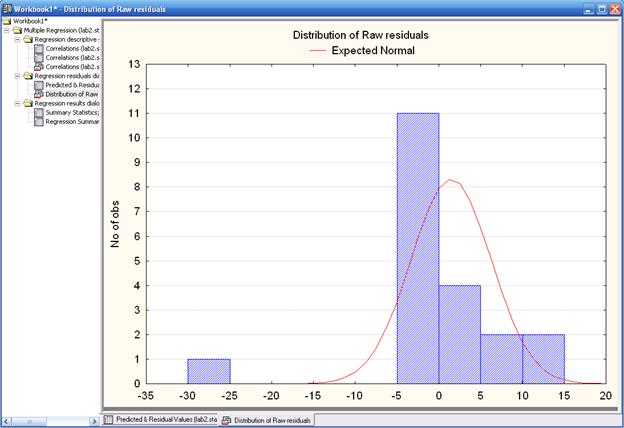
Рис. «График распределения остатков»

 

Лабораторная работа №4

 

Задание

 

По десяти шахтам получены данные, характеризующие процесс добычи угля: мощность пласта X₁(в м), уровень механизации работ X₂ (в %) и сменная добыча угля на одного рабочего Y (в т) (таблица 4).

Требуется:

1. Оценить показатели вариации каждого признака и сделать вывод о возможности применения метода наименьших квадратов для их изучения.

2. Проанализировать линейные коэффициенты парной и частной корреляции.

3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.

4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и . Сравнить значение скорректированного и нескорректированного линейных коэффициентов множественной детерминации.

5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии каждого фактора.

6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

 

 

1.

Сравнивая значения средних квадратических отклонений и средних величин и определяя коэффициенты вариации:

 

V1=20,89; V2=21,169; V3=6,917

 

приходим к выводу о повышенном уровне варьирования признаков, хотя и в допустимых пределах, не превышающих 35%. Совокупность предприятий однородна, и для ее изучения могут использоваться метод наименьших квадратов и вероятностные методы оценки статистических гипотез.

2.

 

Наиболее тесно связаны y и x₁: 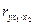=0,868, связь y и x₂ гораздо слабее: 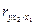=0,0964, а межфакторная зависимость x₁ и x₂ выше, чем парная y и x₂: 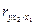=0,0964< 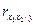=0,0396. Все это приводит к выводу о необходимости исключить фактор x₂ – доля высококвалифицированных рабочих – из правой части уравнения множественной регрессии.

 

3-6.

 

 

Величины и указывают, что с увеличением x₁ и x₂ на единицу их значений результат увеличивается соответственно на 0,766 и на 0,0173.

По данным из таблицы дисперсионного анализа F_факт =20,62. Вероятность случайно получить такое значение F-критерия составляет 0,0011, что не превышает допустимый уровень значимости 5%.

По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат y признака фактора , чем признака фактора 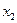: 0,47% против 0,04%.

 

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

Уфимский Государственный Авиационный Технический Университет