Определение резонансных частот колебаний колонны бурильных труб
Теоретические основы работы
Резонансные частоты при колебаниях колонны бурильных труб имеют место при совпадении частот привода и частот собственных колебаний (продольных и крутильных) колонны труб. Особенно опасны резонансы на частоте основного тона 
и частотах первых двух-трех обертонов (
). Рассмотрим отдельно продольные и крутильные колебания.
Продольные колебания колонны бурильных труб имеют место при изменении осевой нагрузки на забой, при котором наблюдается смещение отдельных сечений колонны вдоль ее продольной оси.
Частотное уравнение для этого случая имеет вид:
, (2.1)
где 
- сосредоточенная масса на нижнем конце колонны (в контакте с забоем), равная отношению осевой нагрузки (
) и ускорения силы тяжести; 
- скорость продольной волны в материале колонны; 
- модуль упругости материала труб при растяжении - сжатии; 
- площадь поперечного сечения колонны; 
- ее длина; 
- неизвестная частота собственных колебаний колонны бурильных труб.
Так как уравнение (2.1) является трансцендентным, то оно может иметь бесконечное множество корней (рис.2.1), из которых наибольший интерес представляют два-три первых корня (частота основного типа и первые обертоны).
Уравнение (2.1) представляет собой частотное уравнение для колебательной системы с распределенными параметрами, каковой и является колонна бурильных труб. Решение уравнения (2.1) можно получить графически как совокупность точек пересечения двух функций:
. (2.2)
 |
Рис.2.1. Частотный спектр при продольных колебаниях колонны
бурильных труб
Если эти решения (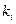
) сопоставить с частотой возмущающей силы 
, представляющей собой частоту привода, то можно получить искомые резонансы при продольных колебаниях колонны, когда 
. Для этого графическое решение уравнения (2.1) необходимо спроецировать на ось абсцисс системы координат, в которой находится графическое решение и изображены функции 
и 
. Второй координатной осью будет ось условных единиц (значений и ). Для перевода частоты привода в частоту вращения колонны используется известное выражение: 
, где 
- частота вращения колонны бурильных труб, об/мин.
Крутильные колебания колонны бурильных труб. Частотное уравнение для крутильных колебаний получается аналогично уравнению (2.1) из волнового уравнения крутильных колебаний, откуда следует:
, (2.3)
где 
- скорость поперечной волны в материале колонны бурильных труб;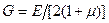 
– модуль касательной упругости; 
- коэффициент Пуассона материала труб; 
- соответственно внешний и внутренний диаметры колонны; 
- неизвестная частота собственных крутильных колебаний колонны.
По аналогии с первым случаем введем следующие обозначения:
. (2.4)
Решениями уравнения будут точки пересечения указанных функций в координатах и условных единицах для 
и 
. Решения (
) проектируются на ось абсцисс, где и определяются резонансные частоты вращения колонны труб (
) с использованием пересчетов по формуле (2.3), в которой необходимо заменить на .
Пример выполнения ргр - 2
Пусть требуется определить собственные частоты колебаний (продольных и крутильных) стальной колонны бурильных труб диаметром 50 мм (
м; 
м; 
Па; удельная плотность материала труб 
кг/м3; 
) при бурении скважины до глубины 
м с осевой нагрузкой 
кН станком ЗИФ-300.
Расчеты по формулам (2.2, 2.4) представим графически (рис.2.2), откуда следует, что 
с-1 (
об/мин) и 
с-1 (
об/мин).
