Определение активной Р и полной S мощности трехфазной системы

Вариант№85.

Задача №1

Задание: На рисунке 1 изображена схема трехфазной цепи. Каждая из них образована трехфазным генератором, который дает трехфазную несинусоидальную систему э.д.с., и равномерной нагрузкой. Даны значения амплитуды э.д.с. фазы А генератора, периода Т и параметров R, L, C.

Необходимо найти:

1. Мгновенное значение напряжения.

2. Построить график этого напряжения в функции времени.

3. Определить действующее значение этого напряжения.

4. Найти активную Р и полную S мощности трехфазной системы.

E_m,B	Т, с	L, мГн	С, мкФ	R, Ом	Найти
	0,01				A,g

Форма э.д.с.:

e_A(t)

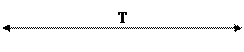Задача1

Решение.

1.Нахождение мгновенного напряжения между точками g и d.

1.1.Так как э.д.с. задана графически, то функцию перед нахождением неизвестных нужно разложить в ряд Фурье.

Для разложения функции в ряд Фурье используем таблицу разложения. Тогда функция примет вид:

Согласно исходным данным Еm=400 В, тогда

1.2. Найдём угловую частоту, зная период.

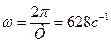1.3.1 Найдём мгновенное значение тока i_ab

Запишем закон Ома для участка цепи

i_ca= u_ca/Z_ca

где u_ca=e_ca

Запишем это уравнение в комплексном виде:

İ_ca=Ė_ca/ Z_ca(1)

Исходя из заданной фазной э.д.с Ė_A₁=324,55 (В);

Ė_A₃=-36,06 (В);

Ė_A₅=12,98 (В);

Вычислим комплексы линейной э.д.с. для каждой из гармоник

для прямой последовательности Ė_С_A₁= Ė_A₁e^j^150º=562,13 e^j^150º(В);

для нулевой последовательности Ė_С_A₃= 0 (В);

для обратной последовательности Ė_С_A₅= Ė_A₁e^-^j^150º=22,48 e^-^j^150º(В);

Вычислим полное сопротивление участка ca для каждой из гармоник

Z_с_a₁= X_L₁+R=j628∙25∙10^-3+12=12+j15.7=19.76 e^j^52.61º(Ом);

Z_ca₃= X_L₃+R=3∙j628∙25∙10^-3+12=12+j47.1=48.6 e^j^75.71º(Ом);

Z_ca₅= X_L₅+R=5∙j∙628∙25∙10^-3+12=12+j78.5=79.41 e^j^81.31º(Ом);

По формуле (1) имеем: İ_ca₁=562,13 e^j^150º/19.76 e^j^52.61º=28.45 e^j^97.39º (А);

İ_ca₃=0 (А);

İ_ca₅=22,48 e^-^j^150º/79.41 e^j^81.3º=0.28 e^-^j^231.3º (А);

1.3.2. Найдём мгновенное значение тока i_bc

i_bc= u_bc/Z_bc

где u_bc=e_bc

İ_bc=Ė_bc/ Z_bc

для прямой последовательности Ė_BC1= Ė_CA₁e^-^j^240º;

для нулевой последовательности Ė_BC3= 0 (В);

для обратной последовательности Ė_BC5= Ė_CA₅e^j^240º;

Z_bc =Z_ca

Тогда İ_bc₁=İ_ca₁e^-^j^240º=28.45e^-^j^142.61º

İ_bc₃= 0

İ_bc₅= İ_ca₅ e^j^240º=0.28 e^j8.7^º

1.4 Найдём напряжение между точками g и d:

_ga= _ca + _cd = İ_bc X_L +İ_ca Zca;

_ga1= _ca1 + _cd1 =28.45e^-j142.61º∙15.7 e^j90º+19.76 e^j52.61º∙28.45 e^j97.39º=228.3 e^j18.91º(В);

_gd₃=0 (В);

_ga₅= _ca₅ + _cd₅ =0.28 e^j^8.7º∙78.5 e^j^90º+79.41 e^j^81.31º∙0.28 e^-^j^231.3º =24.73 e^-^j^25.63º(В);

Построение мгновенного значения напряжения

Запишем мгновенное значение напряжения

u_ga(t)= 228.3sin(ωt+18.91˚)+24.73 sin(5ωt-25.63˚)

Определение действующего значения заданного напряжения.

3.1 Действующее значение несинусоидального напряжения находим по формуле:

Определение активной Р и полной S мощности трехфазной системы.

Для определения полной мощности найдём фазный ток.

4.1Рассмотрим узел а и напишем для него первый закон Кирхгофа:

i_A=i_ab+i_aƠ-i_ca

İ_An= İ_{ab n}+İ_aƠn-İ_can (2)

Для определения фазного тока нужно найти ток i_a_Ơ,i_ab

4.1.1 Найдём ток i_a_Ơ

Напряжение между точками а и Ơ равно фазному поэтому ток равен

i_a_Ơ=e_А/X_C

İ_a_Ơ_n=Ė_An/ X_Cn

İ_a_Ơ1=Ė_A₁/ X_C₁=324.55/63,69e^-^j^90º =5.09e^j^90º (А);

İ_a_Ơ3=Ė_A₃/ X_C₃=-36,06/21,23e^-^j^90º=-1,69e^j^90º(А);

İ_a_Ơ5=Ė_A₅/ X_C₅=12,98/12,74 e^-^j^90º= 1.02e^j^90º(А);

4.1.2. Найдём ток i_ab

для прямой последовательности İ_ab₁ = İ_с_a₁ e^-^j¹²⁰ =28.45 e^j^97.39º e^-^j^120º=28.45 e^-^j^22.61(А);

для обратной последовательности İ_ab₅= İ_с_a₅e^j¹²⁰ =0.28 e^-^j^231.3º e^j^120º=0.28 e^-^j^111.3 (А);

Согласно формуле (2) имеем:

İ_A₁= İ_ab₁+İ_a_Ơ1-İ_ca₁=28.45 e^-^j^22.61º+5.09e^j^90º -28.45 e^j^97.39º = 28.45 e^-^j^{22.6 1º +}5.09e^j^90º-28.45 e^j^97.39º =30-34.11 j=45.43e^-^j^48.67º(А);

İ_A₃= İ_ab₃+İ_a_Ơ3-İ_ca₃= İ_a_Ơ3=-1,69e^j^90º(А);

İ_A₅= İ_ab₅+İ_a_Ơ5-İ_ca₅=0.28 e^-^j^111.3º+ 1.02e^j^90º-0.28 e^-^j^231.3º =0.1+0.5j=

=0.51e^-^j78.7^º(А);

Перейдём к мгновенному значению тока:

i_A(t)=45.43sin(ωt-48.67˚)-1.69sin(3ωt+90˚)+0.51 sin(5ωt-78.7˚)

4.2 Активную мощность определим по формуле:

4.3Полную мощность определим по формуле:

Задача №2

Рассчитать периодический процесс в линейной эл цепи по характеристикам для мгновенных значений и построить графики изменения требуемых величин во времени.

В три плеча мостовой схемы включены линейные сопротивления Z₁, Z₂ Z₃ а в одно плечо - идеальный диод с характеристикой, изображенной на рис2.2. К зажимам с и d схемы присоединен источник синусоидальной ЭДС е=100sinωt.

Построить кривую напряжения между точками a и b во времени. Определить среднее за период значение этого напряжения.

Ом	Д
Z₁ _,_Ом
Z_2, _Ом	3j
Z_3, _Ом

1. Для положительной полуволны диод открыт, потенциал т. а равен потенциалу т. с.

Значит для идеального диода: U g= 0(В)

Uab=Ucb= i3∙Z3

и по закону Ома i3=e/(Z3+Z4)=100sinwt/(4+3j)=20sin(wt-36.8) A

Uab= i3∙Z3=(20sin(wt-36.8))∙3e^j90º=60sin(wt+53.2) B

Для отрицательной полуволны диод закрыт i=0

Uad=Ubb=-i3∙Z4=-(20sin(wt-36.8))∙4=-8020sin(wt-36.8)