Вычисление производной по определению

Практикум 8. Производные.

Приращение функции. Вычисление производных по определению. М-функции (файл-функции)

Символическое вычисление производных. Геометрический смысл производной

Вычисление приращений с использованием M-File.

Приращением функции в точке 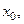соответствующим приращению аргумента называется величина

Упражнение 1. Для функции 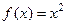создатьM-File, вычисляющий приращение функции в точке при приращениях аргумента С помощью вызова M-File вычислить приращения функции в точках 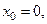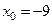при приращениях от 0 до 1 с шагом 0.1.

Рассмотренные ранее M-File представляют собой файл-программы и являются последовательностью команд MatLab, они не имеют входных и выходных аргументов. Для использования численных методов и при программировании собственных приложений в MatLab необходимо уметь составлять собственные файл-функции, которые производят необходимые действия с входными аргументами и возвращают результат в выходных аргументах.

Пример 1. Предположим, что в вычислениях часто приходится использовать функцию Имеет смысл один раз написать файл-функцию, а потом вызывать её всюду, где необходимо вычисление этой функции. Откройте в редакторе

M-File новое окно и наберите текст

 

function f=myfun1(x)

f=exp(-x)*sqrt((x^2+1)/(x^4+0.1));

 

Слово function в первой строке определяет, что данный файл содержит файл-функцию. Первая строка является заголовком функции, в которой размещается имя функции и списки входных и выходных аргументов. В примере myfun1 – имя функции, один входной аргумент х и один выходной аргумент f. После заголовка следует тело функции, которое в данном примере состоит из одной строки, где и вычисляется значение функции. Вычисленное значение записывается в f.

Теперь сохраните файл в рабочем каталоге. Выбор пункту Save или Save as меню приводит к появлению диалогового окна сохранения файла, в поле File name которого уже содержится название myfun1. Не изменяйте его, сохраните файл-функцию в файле с предложенным именем.

Теперь созданную функцию можно использовать так же, как и встроенные sin, cos, exp и другие, например из командной строки.

y=myfun1(1)

 

y =

 

0.4960

Удобно сразу записать функцию так, чтобы она работала с массивами входных данных.

Пример 2. Создадим файл-функцию

function f=myfun2(x)

f=exp(-x).*sqrt((x.^2.+1)./(x.^4.+0.1));

Теперь можно вызвать функцию, для вектора х, получив вектор значений у:

>> x=1:5; y=myfun2(x)

 

y =

 

0.4960 0.0754 0.0175 0.0047 0.0014

 

>>

Упражнение 2. Создать функцию, вычисляющую приращения функции в точке 1 при различных приращениях аргумента. Вычислить приращения функции при приращениях аргумента от -0.5 до 0.5 с шагом 0.05.

 

Вычисление производной по определению.

Файл-функции с несколькими входными аргументами. Работа с файл-функциями с несколькими входными аргументами практически не отличается от случая с одним аргументом.

Пример 3. Создадим файл-функцию, вычисляющую длину радиус-вектора точки трёхмерного пространства

function r=radius(x,y,z)

r=sqrt(x^2+y^2+z^2)

Вычислим длину радиус вектора точки (2;3;5)

r=radius(2,3,5)

 

r =

 

6.1644

Упражнение 3. Создать функцию, зависящую от точки и приращения вычисляющую предел отношения приращения функции к приращению аргумента для функции 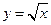. Вычислить отношение приращения функции к приращению аргумента для каждой из точек 1; 0,5; 2 при приращениях аргумента 0,1; 0,01; 0,001.

Функции от функций. Если для исследования функций требуется запрограммировать собственный алгоритм, который должен оперировать с достаточно большим набором функций, то удобно оформить алгоритм в виде файл-функции, входными аргументами которой будут служить другие файл-функции. Имя используемой файл-функции передаётся в строковой переменной, а вычисление производится с помощью команды feval, аргументами которой является сама функция и её аргументы.

Пример 4. Создадим файл-функцию, вычисляющую значение сложной функции при произвольных функциях

function p=cos2(fname,x)

p=cos(feval(fname,x))^2;

 

Затем в командном окне можно вызвать заданную функцию с любой функцией (существующей в MatLab или созданной нами).

p1=pr('sin',0)

 

p1 =

 

p2=pr('myfun1',1)

 

p2 =

 

0.7735

Результаты вычисления равны:

 

 

Упражнение 4. Создать функцию, зависящую от функции, точки и приращения, вычисляющую отношение приращения функции к приращению аргумента. Вычислить значения этой функции в точках 1, 2, при приращениях аргумента 0,001, для функций

Упражнение 5. Создать функцию, зависящую от функции и точки, вычисляющую значение производной функции в точке по определению. Для функций и точек из упражнения 4 вычислить значения производных. Заполнить таблицу, вставив вместо упр4 и упр5 результаты соответствующих упражнений.

 

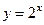
	упр1	упр1	упр1
упр2	упр2	упр2
	упр1	упр1	упр1
упр2	упр2	упр2
	упр1	упр1	упр1
упр2	упр2	упр2