Основы математической статистики

Выборочный метод.

1) В городе А для определения сроков гарантийного обслуживания проведено исследование величины среднего пробега автомобилей (X), находящихся в эксплуатации в течение двух лет с момента продажи автомобиля магазином. Получен следующий результат (тыс. км): 3,0; 14,4; 25; 18,6; 12,1; 10,6; 18; 17,3; 29,1; 20; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6; 25; 20; 14,4; 11,2. Требуется: а) составить ряд распределения частот (вариационный ряд); б) составить ряд распределения относительных частот.

2) По наблюденным данным предыдущей задачи построить многоугольник распределения (полигон частот либо относительных частот).

3) Выборка задана интервальным вариационным рядом:

i	x_i < X < x_i+1	n_i
1	11-14	16
2	14-17	24
3	17-20	30
4	20-23	7
5	23-26	8

Построить гистограммы выборочной оценки плотности вероятности (гистограмму частот и гистограмму относительных частот).

4) Найти числовые характеристики выборки, по данным задачи (1), такие как: размах, моду, медиану, выборочное среднее, выборочную дисперсию, выборочное ср. кв. отклонение.

5) Найти асимметрию и эксцесс по заданному распределению выборки:

	-2

Оценка параметров распределения.

1) Найти несмещенную оценку математического ожидания и дисперсии с.в. Х.

	- 10	-5	- 1

2) Случайная величина X (время работы элемента) имеет показательное распределение. Ниже приведено эмпирическое распределение среднего времени работы п =200 элементов (в первой строке приведено среднее время работы элемента в часах; во второй строке указана частота - количество элементов, проработавших в среднем часов):

	2,5	7,5	12,5	17,5	22,5	27,5

Найти методом моментов точечную оценку неизвестного параметра 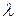показательного распределения.

3) Случайная величина X (ошибка измерения дальности радиодальномером) подчинена равномерному закону распределения с неизвестными параметрами и . Ниже приведено эмпирическое распределение средней ошибки = 200 измерений дальности (в первой строке указана средняя ошибка ; во второй строке указана частота - количество измерений, имеющих среднюю ошибку ):

: 3 5 7 9 11 13 15 17 19 21

:21 16 15 26 22 14 21 22 18 25

Найти методом моментов точечные оценки неизвестных параметров и равномерного распределения.

4) Случайная величина X (число семян сорняков в пробе зерна) распределена по закону Пуассона. Ниже приведено распределение семян сорняков в п = 1000 пробах зерна (в первой строке указано количество сорняков в одной пробе; во второй строке указано - число проб, содержащих семян сорняков):

Найти методом моментов точечную оценку неизвестного параметра распределения Пуассона .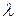

5) Случайная величина X (отклонение контролируемого размера изделия от номинала) подчинена нормальному закону распределения с неизвестными параметрами и . Ниже приведено эмпирическое распределение отклонения от номинала 200-т изделий (в первой строке указано отклонение - (мм); во второй строке приведена частота - количество изделий, имеющих отклонение ): 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9 2,2 2,3

6 9 26 25 30 26 21 24 20 8 5

Найти методом моментов точечные оценки неизвестных параметров и нормального распределения.

6) Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 ч. Найти с надежностью 0,95 доверительный интервал для средней продолжительности а горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы = 40 ч. Предполагается, что продолжительность горения ламп распределена нормально.

7) Из генеральной совокупности извлечена выборка объема п = 12:

варианта : - 0,5 - 0,4 - 0,2 0 0,2 0,6 0,8 1 1,2 1,5

частота : 1 2 1 1 1 1 1 1 2 1

Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупностис помощью доверительного интервала.

8) По данным выборки объема п из генеральной совокупности нормально распределенного количественного признака найдено «исправленное» среднее квадратическое отклонение s. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение с надежностью 0,999, если: а) п =10, s = 5,l; б) п = 50, s =14.

Проверка статистических гипотез.

1) Коэффициенты газоотдачи из обводненных зон для «Челбасского», «Каневского» и «Ленинградского» газоконденсатных месторождений Краснодарского края равны соответственно 0,78; 0,73; 0,69. Считая, что = 0,10, проверить гипотезу о том, что среднее значение коэффициента газоотдачи может быть выбрано равным 1. Предполагается, что случайная величина - коэффициент газоотдачи - подчинена нормальному закону распределения.

2) Эффективное применение вихревого эффекта в установках низкотемпературной сепарации газоконденсатных смесей требует исследования зависимостей температурных перепадов в вихревой трубе от давления потока при фиксированных режимных и конструктивных параметрах. При изучении характеристик и температурных режимов вихревой трубы изменяли давление, с которым поток газа входит в трубу , и диаметр сопла, через которое выходит охлажденный поток. При этом были получены результаты:

Сопло 1, = 4 кгс/см²

- температурные перепады

20,8

20,5

21,6

19,3

25,2

4,6

6,2

9,4

Сопло 2, = 6,5 кгс/см²

- температурные перепады

4,6

6,2

9,4

Требуется проверить гипотезу о точности измерения охлаждающей способности вихревой трубы, а именно: что дисперсия величины не меняется при изменении условий опыта.

3) При построении модели управления процессом переработки нефти необходимо проверять нормальность распределения выходной величины температуры разделения фракции бензин - авиакеросин. Было проведено 81 измерение значений температуры раздела:

Проверить гипотезу по критерию - Пирсона о нормальном распределении величины температуры раздела бензина и авиакеросина - .

Элементы теории корреляции.

1) Известны результаты наблюдений за свойствами горных пород, Р0 () – предел текучести по штампу; Рш (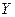) - твердость по штампу. Найти коэффициент корреляции между Р0 и Рш. Получить уравнение линейной регрессии Рш на Р0. Проверить гипотезу о значимости коэффициента корреляции при уровне значимости α = 0,05.

2) Дана корреляционная таблица для значений статистически связанных параметров нефтяных скважин: забойного (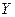) и пластового () давлений фонтанирующих скважин:

Результаты 60 измерений

\
			-		-	-
	-				-	-
	-	-				-
	-	-			-
	-	-	-	-	-	-
	-	-	-	-	-
							= 60

Построить уравнение линейной регрессии, описывающей статистическую зависимость 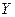- забойного и - пластового давлений фонтанирующих скважин. Проверить гипотезу о значимости коэффициента корреляции при 5 % - ом уровне значимости.