Отчет по лабораторной работе
«Статистические методы исследований»
Исполнитель: Миронов А.А.
Специальность: 03.02.08 – « Экология»
Преподаватель: проф. Пименов. В.И.
Санкт-Петербург
Введение
Целью статистического исследования зависимостей является построение математической модели объекта. Ее знание необходимо для прогнозирования поведения или свойств объекта
При построении статистических моделей объект рассматривается как «черный ящик», а реальные взаимосвязи аппроксимируются некоторыми зависимостями.
Входные переменные или признаки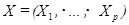 
называют независимыми переменными, факторами. Выходные переменные 
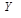характеризуют, например, физические и химические свойства производимого продукта или технико-экономические показатели процесса. Их называют зависимыми переменными или откликами. Случайные компоненты 
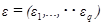отражают влияние неучтенных на “входе” факторов, например, изменение характеристик оборудования вследствие износа, присутствие случайных примесей, а также случайные ошибки в измерении Y.
Конечной целью статистического исследования зависимостей является построение математической модели объекта
,
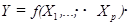которое осуществляется по результатам n измерений входных и выходных переменных (Xi, Yi), i=1,..., n.
Задание №1. Первичная статистическая обработка: расчет выборочных характеристик, интервальная оценка параметров:
1) Привести названия выборочных характеристик на русском языке и их значения;
2) Привести графики гистограммы и эмпирической функции распределения для каждого из параметров X 2 и Y;
3) Записать в математической форме 95%-е доверительные интервалы для математических ожиданий mx2, my(например, 73.67<mx2 <75.63) и стандартных отклонений sx2,sy;
4) По стандартизованным величинам асимметрии A и эксцесса E сделать предположения о виде законов распределения параметров X2, Y.
1. Расчет основных и дополнительных выборочных характеристик для параметров X2 и Y
В табл. 1 представлены исходные данные для статистической обработки.
Таблица 1 – Исходные данные (вариант №15)
X1 X2 Y
25 66,0585 9,00123199376
26 42,0645 8,33569368849
27 39,5099 7,72719036745
28 44,3478 8,5235277758
29 53,0357 8,77742131898
30 42,8061 8,7069923663
31 39,1771 8,41498032872
32 51,8017 9,44260712517
33 47,0298 8,90801474431
34 51,2993 9,11110558875
35 63,2825 9,944641313
36 57,7105 10,0191279286
37 63,2398 10,3956277183
38 53,7431 9,85547580822
39 55,9805 9,9345447396
40 42,3791 9,37107992877
41 37,2077 9,07062956999
42 53,9396 10,1549859105
43 49,4274 10,1206430538
44 48,4345 9,94833000755
45 63,8514 11,0708674878
46 45,8418 10,0476317995
47 37,0302 9,25618207697
48 46,7369 10,1621247391
49 39,4807 9,86962108036
50 47,8018 10,5404754453
51 45,3467 10,2176414974
52 47,0218 10,3268487612
53 43,5582 10,1974533169
54 46,6813 10,5390882191
55 51,5947 10,8024021996
56 35,8886 9,63179457429
57 42,2585 10,0588443074
58 52,1683 10,8834031989
59 54,3159 11,1431298845
60 50,2236 11,1672965903
61 52,9705 11,4804739453
62 53,4466 11,4535931696
63 43,9447 10,6270501066
64 59,1381 12,0494980357
65 57,303 12,0056316316
67 45,3918 10,9333924023
68 35,7222 10,4246166881
69 56,9479 11,9883181499
70 60,3098 12,1208607867
71 39,6918 10,8818226282
72 41,0465 11,2629718612
73 45,2616 11,1806934725
Проведем расчет основных и дополнительных выборочных характеристик для параметров X2 и Y.
Необходимые процедуры собраны в разделе Describe=>NumericData=>One-Variable Analysis. Выборочные точечные характеристики рассчитываются табличной процедурой Summary Statistics.
В табл.2 представлены результаты расчета точечных характеристик для параметров X2 и Y
Таблица 2-. Результаты расчета точечных характеристик для параметров X2 и Y
| Х2 | Y | ||
| Count | Кол-во | 48,0 | 48,0 |
| Average | Среднее | 48,8219 | 10,1685 |
| Variance | Дисперсия | 62,6234 | 1,10964 |
| Standard deviation | Стандартное отклонение | 7,9135 | 1,05339 |
| Minimum | Минимальное значение | 35,7222 | 7,72719 |
| Maximum | Максимальное значение | 66,0585 | 12,1209 |
| Range | Размах значений | 0,906348 | -0,37558 |
| Stnd. skewness | Стандартизованная асимметрия | -0,904617 | -0,59267 |
| Stnd. kurtosis | Стандартизованный эксцесс | 2343,45 | 488,088 |
| Sum | Сумма всех замеров переменной | 48,0 | 48,0 |
2. Построить гистограммы и эмпирические функции распределения для параметров X2 и Y
Построение гистограммы для выбранной переменной осуществляется процедурой Frequency Histogram после выбора инструмента Graphics Options.
График Fn(x) эмпирической функции распределения строится установкой в том же контекстном меню режимов Relative, Cumulative и Poligon вместо заданного по умолчанию режима Histogram.
На рис. 1 представлены гистограммы распределения параметров X2 и Y.
На рис. 2 представлены эмпирические функции распределения параметров X2 и Y.
 |  | ||
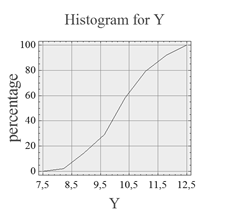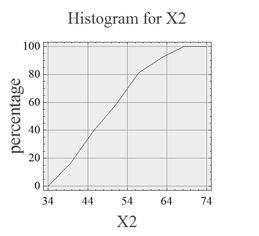Рисунок 1. — Гистограммы распределения параметра X2 и Y
Рисунок 2. — Эмпирические функции распределения параметров X2 и Y
3. Для параметров X 2 , Y построить в пакете Statgraphics 95% -ое доверительные интервалы: для математического ожидания и для стандартного отклонения
В табл.3 отображены значения доверительных интервалов для среднего значения и стандартного отклонения параметров X2 и Y.
Таблица 3 – значения доверительных интервалов для среднего значения и стандартного отклонения параметров X2 и Y.
| 95%-е доверительные интервалы для среднего значения, m | 95%-е доверительные интервалы для стандартного отклонения, s | |
| X2 | 46,524≤m<51,1197 | 6,58774 ≤s<9,91229 |
| Y | 9,86262≤m<10,4744 | 0,876917 ≤s<1,31946 |
Вывод по результатам расчета для параметров X2 и Y.
В данной таблице приведены сводные статистические данные по параметрам X1, X2 и Y. Особый интерес здесь представляют стандартизованная асимметрия и стандартизованный эксцесс, которые могут быть использованы для определения закона распределения. В нашем случае значения этих статистических данных для параметров X1, X2 и Y лежат в пределах диапазона:
· Доверительный интервал для среднего значения x2 находится где-то между 46,524
и 51,1197, а для стандартного отклонения где-то между 6,58774 и 9,91229;
· Доверительный интервал для среднего значения y находится где-то между 9,86262 и 10,4744, а для стандартного отклонения где-то между 0,876917 и 1,31946.
Эти полученные данные указывают на нормальное распределение величин X2 и Y.
Задание №2. Расчет парных корреляций:
1) создать новые переменные типа x1x1, x1x2, x2x2;
2) выполнить анализ полных парных связей;
3) проанализировать коэффициенты корреляции для всех возможных пар переменных, содержащих Y.
Создание новых переменных
Для задания имени новой переменной нужно последовательно выделить заголовок пустого столбца и в контекстном меню (после щелчка правой клавишей мыши) выбрать Modify Column, после чего в поле Name ввести одно из указанных имен. Создание столбца со значениями новой переменной, которые вычисляются через выражение для ранее созданных переменных выполняются с помощью команды Generate Data из контекстного меню. Задать выражения вида x1*х1, x1*x2, x2*х2. В табл.4 представлены новые переменные для анализа.
Таблица 4 - Новые переменные для анализа
| № | X1 | X2 | Y | X1X1 | X1X2 | X2X2 |
| 66,0585 | 9,00123199376 | 1651,4625 | 4363,72542225 | |||
| 42,0645 | 8,33569368849 | 1093,677 | 1769,42216025 | |||
| 39,5099 | 7,72719036745 | 1066,7673 | 1561,03219801 | |||
| 44,3478 | 8,5235277758 | 1241,7384 | 1966,72736484 | |||
| 53,0357 | 8,77742131898 | 1538,0353 | 2812,78547449 | |||
| 42,8061 | 8,7069923663 | 1284,183 | 1832,36219721 | |||
| 39,1771 | 8,41498032872 | 1214,4901 | 1534,84516441 | |||
| 51,8017 | 9,44260712517 | 1657,6544 | 2683,41612289 | |||
| 47,0298 | 8,90801474431 | 1551,9834 | 2211,80208804 | |||
| 51,2993 | 9,11110558875 | 1744,1762 | 2631,61818049 | |||
| 63,2825 | 9,944641313 | 2214,8875 | 4004,67480625 | |||
| 57,7105 | 10,0191279286 | 2077,578 | 3330,50181025 | |||
| 63,2398 | 10,3956277183 | 2339,8726 | 3999,27230404 | |||
| 53,7431 | 9,85547580822 | 2042,2378 | 2888,32079761 | |||
| 55,9805 | 9,9345447396 | 2183,2395 | 3133,81638025 | |||
| 42,3791 | 9,37107992877 | 1695,164 | 1795,98811681 | |||
| 37,2077 | 9,07062956999 | 1525,5157 | 1384,41293929 | |||
| 53,9396 | 10,1549859105 | 2265,4632 | 2909,48044816 | |||
| 49,4274 | 10,1206430538 | 2125,3782 | 2443,06787076 | |||
| 48,4345 | 9,94833000755 | 2131,118 | 2345,90079025 | |||
| 63,8514 | 11,0708674878 | 2873,313 | 4077,00128196 | |||
| 45,8418 | 10,0476317995 | 2108,7228 | 2101,47062724 | |||
| 37,0302 | 9,25618207697 | 1740,4194 | 1371,23571204 | |||
| 46,7369 | 10,1621247391 | 2243,3712 | 2184,33782161 | |||
| 39,4807 | 9,86962108036 | 1934,5543 | 1558,72567249 | |||
| 47,8018 | 10,5404754453 | 2390,09 | 2285,01208324 | |||
| 45,3467 | 10,2176414974 | 2312,6817 | 2056,32320089 | |||
| 47,0218 | 10,3268487612 | 2445,1336 | 2211,04967524 | |||
| 43,5582 | 10,1974533169 | 2308,5846 | 1897,31678724 | |||
| 46,6813 | 10,5390882191 | 2520,7902 | 2179,14376969 | |||
| 51,5947 | 10,8024021996 | 2837,7085 | 2662,01306809 | |||
| 35,8886 | 9,63179457429 | 2009,7616 | 1287,99160996 | |||
| 42,2585 | 10,0588443074 | 2408,7345 | 1785,78082225 | |||
| 52,1683 | 10,8834031989 | 3025,7614 | 2721,53152489 | |||
| 54,3159 | 11,1431298845 | 3204,6381 | 2950,21699281 | |||
| 50,2236 | 11,1672965903 | 3013,416 | 2522,40999696 | |||
| 52,9705 | 11,4804739453 | 3231,2005 | 2805,87387025 | |||
| 53,4466 | 11,4535931696 | 3313,6892 | 2856,53905156 | |||
| 43,9447 | 10,6270501066 | 2768,5161 | 1931,13665809 | |||
| 59,1381 | 12,0494980357 | 3784,8384 | 3497,31487161 | |||
| 57,303 | 12,0056316316 | 3724,695 | 3283,633809 | |||
| 45,3918 | 10,9333924023 | 3041,2506 | 2060,41550724 | |||
| 35,7222 | 10,4246166881 | 2429,1096 | 1276,07557284 | |||
| 56,9479 | 11,9883181499 | 3929,4051 | 3243,06331441 | |||
| 60,3098 | 12,1208607867 | 4221,686 | 3637,27197604 | |||
| 39,6918 | 10,8818226282 | 2818,1178 | 1575,43898724 | |||
| 41,0465 | 11,2629718612 | 2955,348 | 1684,81516225 | |||
| 45,2616 | 11,1806934725 | 3304,0968 | 2048,61243456 |
Анализ полных парных связей
Матрица парных коэффициентов корреляции вычисляется в разделе Describe / Numeric Data / Multiple Variable Analysis, с помощью табличной процедуры Correlations. Ввести анализируемые векторы данных y, x1, x2, x1x1, x1x2, x2x2, соответствующие исследуемым переменным. Результаты анализа представлены в табл.5.
Таблица 5 – Результаты анализа полных парных связей
| y | x1 | x2 | X1 X1 | X2 X2 | X1 X2 | |
| у (r) | 0,8593 | 0,3932 | 0,8377 | 0,3777 | 0,9791 | |
| у (n) | ||||||
| у (α) | 0,0057 | 0,0081 |
Проанализировать коэффициенты корреляции для всех возможных пар переменных, содержащих y.
Входная переменная x1: r→1 (приaвыч =0) связь между переменными положительная (прямая, величины х1 и Y с точностью до случайных погрешностей одновременно возрастают или убывают). Для сочетаний y и x1, aвыч меньшие 0.05, означают возможную значимость соответствующих связей, т.е.связь положительная;
Входная переменная X1 X2: r→1 (при aвыч =0) связь между переменными положительная (прямая, величины X1 X2 и Y с точностью до случайных погрешностей одновременно возрастают или убывают); Для сочетаний y и X1 X2, aвыч меньшие 0.05, означают возможную значимость соответствующих связей.
Входная переменная X1 X1: r→1 (приaвыч =0) связь между переменными положительная (прямая, величины X1 X1 и Y с точностью до случайных погрешностей одновременно возрастают или убывают); Для сочетаний y и X1 X1, aвыч меньшие 0.05, означают возможную значимость соответствующих связей, т.е.связь положительная;
Входная переменная X2 X2: r→1 (приaвыч =0) связь между переменными положительная (прямая, величины X2 X2 и Y с точностью до случайных погрешностей одновременно возрастают или убывают); Для сочетаний y и X2 X2, aвыч меньшие 0.05, означают возможную значимость соответствующих связей, т.е.связь положительная;
Входная переменная x2: r→1 (приaвыч =0) связь между переменными положительная (прямая, величины х2 и Y с точностью до случайных погрешностей одновременно возрастают или убывают); Для сочетаний y и X2, aвыч меньшие 0.05, означают возможную значимость соответствующих связей, т.е.связь положительная;
Задание № 3. Многофакторный регрессионный анализ:
1) выполнить пошаговую регрессию;
2) выполнить дисперсионный анализ выбранной модели регрессии.
