Лабораторная работа № 12
Тема: Электронная таблица Microsoft Excel. Методы решения систем линейных алгебраических уравнений (СЛАУ)
Содержание:
Матричные (групповые) операции.. 1
Операции с матрицами. 1
Сложение матриц. 1
Умножение матрицы на число. 2
Методы решения СЛАУ.. 2
Метод Крамера. 3
Матричный способ решения. 3
Задания по лабораторной работе. 3
Задание 1. Решение системы линейных алгебраических уравнений. 3
Контрольные вопросы.. 5
Матричные (групповые) операции
Табличные формулы или формулы массива – очень мощное вычислительное средство Excel, позволяющее работать с блоками рабочего листа как с отдельными ячейками. Табличные формулы в качестве результата возвращают массив значений. Поэтому перед вводом такой формулы необходимо:
þ выделить диапазон ячеек, куда будут помещены результаты;
þ набрать формулу;
þ по окончании ввода нажать комбинацию клавиш Ctrl+Shift+Enter!!!
Формула вводится во все ячейки выделенного интервала. При активизации любой ячейки из интервала, содержащего формулу массива, в строке формул отображается введенная формула, заключенная в фигурные скобки. Именно фигурные скобки являются признаком табличной формулы. Для выделения всего блока, содержащего табличную формулу, необходимо выделить одну из его ячеек, после чего нажать комбинацию клавиш Ctrl+/. Невозможно редактировать содержимое только одной ячейки из интервала с табличной формулой. Изменить можно только весь блок целиком, для чего он и должен быть предварительно выделен.
Операции с матрицами
К простейшим операциям с матрицами принято относить следующие:
þ сложение и вычитание матриц,
þ умножение и деление матрицы на число,
þ перемножение матриц,
þ транспонирование,
þ вычисление обратной матрицы.
Умножение (деление) матрицы на число, сложение (вычитание) матриц в Excel реализуются достаточно просто: с помощью обычных формул (поэлементное сложение или вычитание, умножение или деление на число), либо с использованием табличных формул, как это описано ниже.
Сложение матриц
Например, пусть необходимо сложить две матрицы размера 3 ´ 3.
Элементы первой матрицы (9 элементов) разместим в интервале A1:C3, второй – в диапазоне E1:G3. Под результат выделим интервал A5:C7. После чего, не снимая выделения, введем формулу =A1:C3+E1:G3, нажав комбинацию клавиш Ctrl+Shift+Enter. В ячейках интервала A5:C7 отобразится результат – сумма соответствующих элементов матриц, а в строке формул мы увидим {=A1:C3+E1:G3}.
Умножение матрицы на число
Пусть вместо сложения нам надо умножить первую матрицу на число 2. Для этого перемещаемся внутрь интервала A5:C7, выделяем его, нажав комбинацию Ctrl+/, вносим в формулу исправления =A1:C3*2 и нажимаем Ctrl+Shift+Enter. В интервале A5:C7 увидим результат умножения, а в строке формул – табличную формулу {=A1:C3*2}.
Для остальных матричных операций в Excel предусмотрены функции:
| МОПРЕД(матрица) | вычисление определителя матрицы |
| МОБР(матрица) | вычисление обратной матрицы |
| МУМНОЖ(матрица1;матрица2) | произведение матриц |
| ТРАНСП(матрица) | транспонирование матрицы |
Первая из этих функций в качестве результата возвращает число (определитель матрицы), поэтому вводится как обычная формула (Enter). Последние три возвращают блок ячеек, поэтому должны вводиться как табличные формулы (Ctrl+Shift+Enter).
Методы решения СЛАУ
Cистему линейных уравнений вида:

принято называть системой n линейных алгебраических уравнений (СЛАУ) с n неизвестными. При этом произвольные числа aij (i = 1, 2,…, n; j = 1, 2,…, n) называются коэффициентами системы (коэффициентами при неизвестных), а числа bi (i = 1, 2,…, n) – свободными членами. Такая форма записи алгебраической линейной системы называется нормальной. Решением СЛАУ называется совокупность чисел xi (i = 1, 2,…, n), при подстановке которых в систему каждое из ее уравнений обращается в тождество.
Систему можно записать в матричной форме AX=B, где A – матрица коэффициентов при неизвестных (матрица системы):

| 
| 
|
X – вектор-столбец неизвестных, B – вектор-столбец свободных членов, целое число n называется размерностью системы. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет больше одного решения.
Метод Крамера (методом вычисления определителей).
Решение СЛАУ можно найти по формулам Крамера
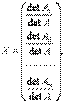
где det A = |A| – определитель матрицы системы (главный определитель), det Ai = | Ai | (i = 1, 2, …, n)– определители матриц Ai (вспомогательные определители), которые получаются из A заменой i -го столбца на столбец свободных членов B. Линейная алгебраическая система несовместна (не имеет решений), если det A =0.
Матричный способ решения
Матричный способ решения СЛАУ достаточно прост. Обе части матричного равенства AX=B умножим слева на обратную матрицу А -1. Получим A -1 ´A´X = A -1 ´B. Т.к. A -1 ´A = E, где E – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы запишется в следующем виде X = A -1 ´B Т.е. для решения системы необходимо найти для матрицы A обратную A -1 и умножить ее справа на вектор-столбец B свободных членов.
Для реализации этого метода в Excel необходимо воспользоваться функциями МУМНОЖ(матрица1;матрица2) и МОБР(матрица).






