НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
________________
Наименование института ЭНИН
Наименование специальности Теплоэнергетика и теплотехника
Наименование выпускающей Автоматизация теплоэнергетических
кафедры процессов
Отчет № 8 по дисциплине «Математические основы теории управления»
Методы решения алгебраических уравнений в системе MathCAD
Вариант 8
Исполнители, студенты группы 5Б13 Опарин А.О ________
Щеголихин ________
Руководитель Кац М.Д. ________
подпись
Томск – 2013
Цель работы
Цель работы заключается в освоении методов расчета корней алгебраических уравнений и систем в MathCAD.
Задачами лабораторной работы являются:
- вычисление корней полиномиального алгебраического уравнения.
- решение одного уравнения с одним неизвестным.
- поиск корней нелинейной системы алгебраических уравнений.


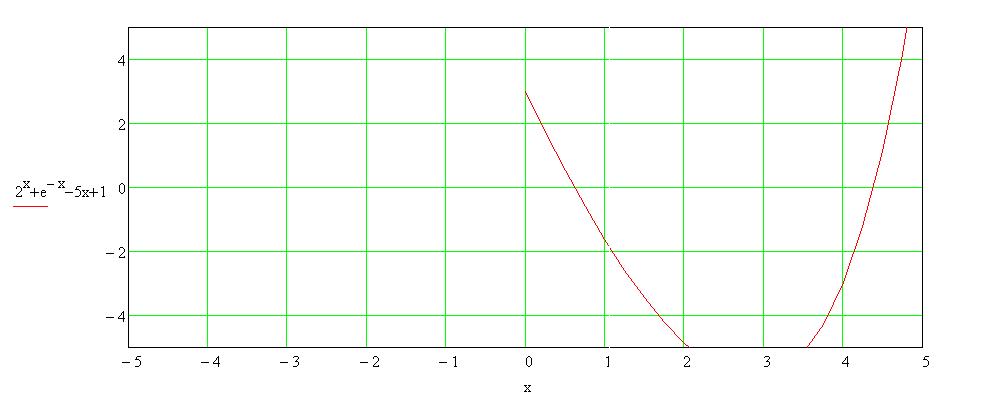


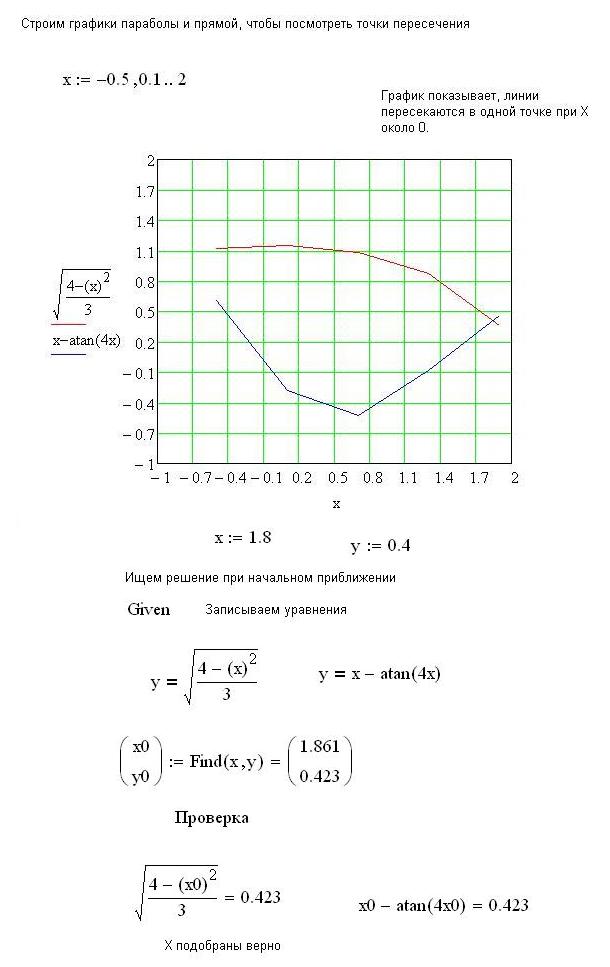
Контрольные вопросы
1. Необходимым условием экстремума функции двух переменных является равенство нулю вектора-градиента этой функции.
Достаточное условие вытекает из знакоопределенности матрицы Гесса.
Достаточным условием минимума функции является положительная определенность матрицы Гесса. Это означает: все главные миноры матрицы Гесса должны быть строго положительными.
Достаточным условие максимума функции является отрицательная определенность матрицы Гесса. Это означает: четные главные миноры матрицы Гесса должны быть положительными, а нечетные – отрицательные.
Если условия положительной и отрицательной определенности не выполняются, а все главные миноры отличны от нуля, то исследуемая функция не имеет экстремума.
2. Mathcad снабжен специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований.
Для символьных вычислений с помощью команд предназначено меню Symbolics (Символика), объединяющее математические операции, которые MathCAD умеет выполнять аналитически.
3. - Щелкнуть мышью там, где надо построить график.
- Выбрать из меню Graph панели инструментов “x-y Plot”. Появляется пустой график с шестью полями ввода.
- Пустое поле в середине горизонтальной оси предназначено для независимой переменной графика.
- Другие четыре пустых поля могут использоваться, чтобы отменить автоматический выбор границ на осях координат.
- Чтобы построить несколько независимых кривых на одном графике вводятся два и более выражения, отделяемые запятыми друг от друга
- В появившемся графике заполняем значение аргумента и функции щелкаем мышью на пустом месте. Появляется функция.
4. Можно. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент.
5. Проверку следует проводить для того, чтобы проверить правильность нахождения корней уравнения.






