Общие сведения
Сила резания может быть вычислена с помощью эмпирической зависимости
, (1.1)
где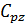 
- коэффициент учитывающий физико механические свойства материала; 
- глубина резания; 
– подача; 
- скорость главного движения резания; 
, 
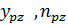– показатели степени.
Измерение силы резания
Для перевода показаний милливольтметра в единицы измерения силы, Н, необходимо произвести операцию его градуирования. Данные представлены в таблице 1.
Таблица 1
Данные градуирования динамометра
| Номер измерения | Показание динамометра, дел | Значение силы Рz | Показание милливольтметра n, дел |
| 5,6 | |||
| 6,3 | |||
| 7,2 | |||
| 8,0 | |||
| 8,8 | |||
| 9,4 | |||
| 10,0 | |||
| 9,4 | |||
| 8,8 | |||
| 8,0 | |||
| 7,2 | |||
| 6,3 | |||
| 5,6 |
Определение цены деления k производится в среде программы Mathcad.
|
|
|
|
|
Здесь x – столбец показаний кольцевого динамометра, дел; y – показание милливольтметра, дел; Z –коэффициент, показывающий сколько делений вольтметра соответствуют единице силы, Н/дел.
Рис.2.Градуировочный график
Экспериментальное нахождение зависимости силы резания
1)Для нахождения численных значений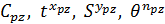 
проводят три опыта, в котором один из элементов режима резания (
) принимают за переменную, а два других – неизменны. Константу 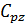удобно представить в виде еi, это удобно для логарифмирования о котором пойдёт речь далее.
В Mathcad это делается так:
Составим матрицу А, в которую запишем результаты экспериментов по определению сил резания:
N – номер измерения; Ср –константа; t - глубина резания, мм; S0 - подача, мм/об; n - скорость главного движения резания,об/мин; nдел - показание милливольтметра, дел
Удалим лишние столбцы и строки, перейдя к матрице АА:
Переведем столбец n из об/мин в рад/сек (AA<4:
2) Логарифмируя зависимость (1.1) в трёх случаях (
получаем три уравнения:
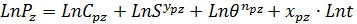
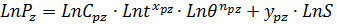
Эти уравнения представляют собой уравнения прямой линии (рис. 3 а,б,в).Представив 
в виде еi мы найдем степенной показатель i.
Из эксперимента мы знаем 
, , , , причем варьировались параметры элементов сил резания каждый по 5 раз. Таким образом имеем 15 уравнений и 4 неизвестных – i, , 
, 
.
В Mathcad это делается так:
Запишем матрицу АА, преобразуем ее в такой вид, что от каждого элемента
будет взят натуральный логарифм ln. Обозначим новую матрицу LnAA.
Преобразуем матрицу АА в ААА,убрав последний столбец, а также преобразуем ее в такой вид, что от каждого элемента будет взят натуральный логарифм ln. Обозначим новую матрицу LnAAА. Убраный столбец запишем отдельно. ln(AA<5>) - столбец натуральных логарифмов сил резания Pz
а)
б) в)
Рис.3.Графики зависимоcти в логарифмических координатах: а) Pz –t б)Pz -S0 в) Pz -n.
Рассчитаем значения степенных показаний. Для этого используем встроенную функцию lsolve
|
Столбец решений показывает значение i, xpz, ypz, npz соответственно.
Значение npz крайне мало, считаем, что npz = 0.
Подставляем значения в формулу (1.1)
Н
Вывод: В ходе работы было выявлено, что скорость главного движения резания не оказывает никакого влияния на главную составляющую силы резания . Важную роль играет подача S и глубина резания t, а сам материал определяется коэффициентом 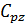, что непосредственно отражается на его обработке.
