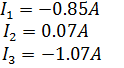Содержание
Введение
Курсовая работа посвящена изучению и использованию различных методик для анализа цепей постоянного и переменного тока, а также для расчета переходных процессов в цепях постоянного тока, содержащих индуктивности и емкости.
Данная курсовая работа включает в себя расчет цепи постоянного тока, расчет цепи переменного тока (четырехполюсник). В каждом разделе необходимо найти токи во всех ветвях схемы. Расчет токов производится различными методами. При постоянном токе это метод законов Кирхгофа, метод наложения источников, метод контурных токов, метод узловых напряжений и метод эквивалентного генератора (для расчета тока в одной ветви).
При переменном токе - это метод комплексных амплитуд, расчет параметров реактивных элементов. Значение тока в каждой ветви, рассчитанное тем или иным методом, не должно быть различным.
Правильность расчетов можно проверить с помощью баланса мощности.
И для каждого задания выполнить моделирование цепи постоянного и переменного тока в среде Multisim.
Техническое задание:
Задание 1.
Задана цепь постоянного тока (Рисунок 1)
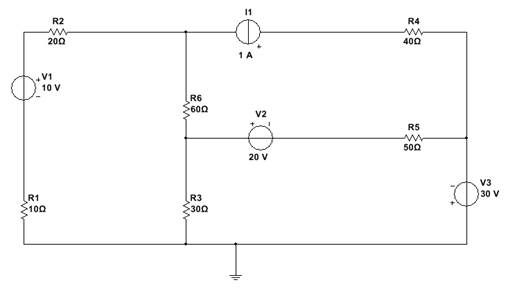
Рисунок 1. Исходная схема.
Параметры элементов:
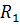= 10 Ом; 
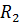= 20 Ом; 
= 30 Ом; 
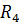= 40 Ом; 
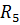= 50 Ом; 
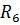= 60 Ом;
= 10 В; E2= 20 В; Е3= 30 В;
J1= 1 А
Необходимо:
1) Рассчитать токи во всех ветвях цепи, используя следующие методы:
а) метод законов Кирхгофа;
б) метод контурных токов;
в) метод узловых напряжений;
г) метод наложения источников
(На каждом этапе для нахождения токов ветвей применять эквивалентные преобразования);
2) Проверить выполнение условие баланса мощностей для цепи;
3) Найти напряжение на резисторе R6, используя методом эквивалентного генератора (источника);
4) Выполнить моделирование цепи в среде Multisim.
Задание 2.
Задан четырехполюсник (Рисунок 2)
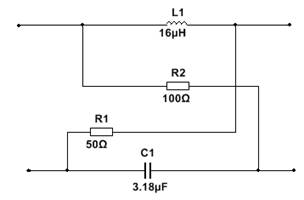
Рисунок 2. Исходная схема.
Сопротивление элементов:
R1 = 50 Ом; R2 = 100 Ом;
На частоте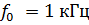 
: 
; 
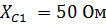
Необходимо:
1) Рассчитать параметры реактивных элементов.
2) Построить векторную диаграмму цепи на частоте .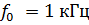
3) Рассчитать токи и напряжения в цепи (на частоте 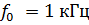) методом комплексных амплитуд.
4) Найти:
а) комплексную частотную характеристику передачи цепи по напряжению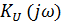 
;
б) амплитудно-частотную характеристику (АЧХ) цепи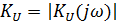 
и построить ее график;
в) фазо-частотную характеристику (ФЧХ) цепи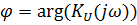 
построить ее график;
г) по графикам определить частоты характерных точек.
5) Выполнить моделирование цепи в среде Multisim.
Задана цепь постоянного тока
1.1. Рассчитать токи во всех ветвях цепи, используя следующие методы:
А Метод законов Кирхгофа
Рисунок 3. Схема для расчета методом законов Кирхгофа.
Метод законов Кирхгофа базируется на 1-ом и 2-ом законах Кирхгофа (ЗIК и ЗIIК).
Количество уравнений соответственно:
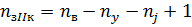
где 
- число узлов в схеме
- количество ветвей в схеме
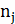- количество ветвей с источником тока
Расставляем произвольно направления токов в схеме
Определяем количество ветвей и количество узлов, а также количество ветвей с источником тока и определяем количество уравнений:
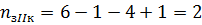
Составляем уравнения по ЗIК:
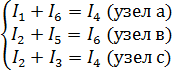
Составляем уравнения по ЗIIК:
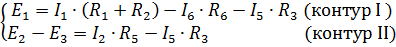
Из уравнения 5 выражаем 
:
; 
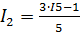
Подставляем в уравнение (2):
Выражаем 
:
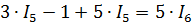
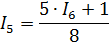
Подставляем и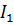 
в уравнение (4), и находим 
:
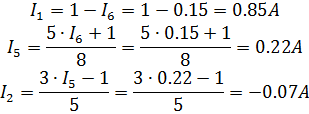
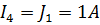
Полученные токи в ветвях:
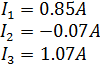
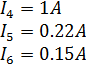
Б. Метод контурных токов
Обозначим контуры:
Рисунок 4. Схема для расчета методом контурных токов.
Метод контурных токов основан на втором законе Кирхгофа. Данный метод позволяет рассчитать схему без преобразований.
Алгоритм расчета:
· Расставляем произвольным образом направление токов в схеме.
· Определяем количество независимых контуров, задаем направление контурных токов.
· Определяем собственные и взаимные сопротивления каждого контура, а так же собственные ЭДС каждого контура.
Нужно составить
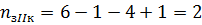уравнения по 2 закону Кирхгофа:
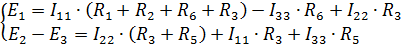
Ток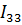 
равен току источника тока, т.е.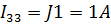 
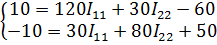
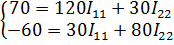
Вычтем из (1) уравнения (2):
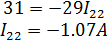
Выразим из (1)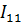 
:
Найдем токи в ветвях:
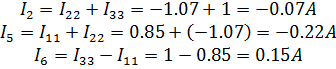
Полученные токи в ветвях:
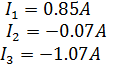
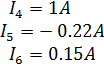
В. Метод узловых напряжений
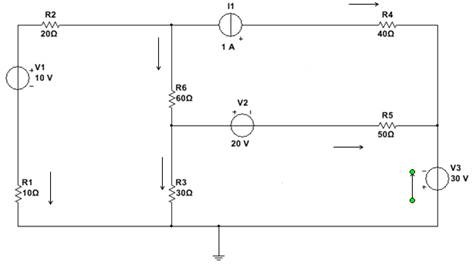
Рисунок 5. Схема для расчета методом узловых напряжений
Метод без преобразования схемы. Определение узловых потенциалов по уравнениям законов токов Кирхгофа. Определение токов в ветвях по закону Ома.
Алгоритм расчета:
) Обозначаем все токи и узлы в схеме
) Принимаем один из узлов за базисный (потенциал этого узла будет равен нулю)
Примем потенциал точки d равным нулю. 
.
Тогда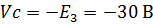 
Составим для узлов а и в уравнение по первому закону Кирхгофа:
Выгрузим токи через потенциал узлов:
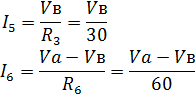
Подставим в систему:
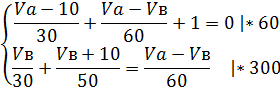
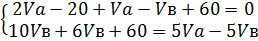
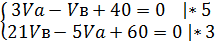
Сложим уравнения (1) и (2):
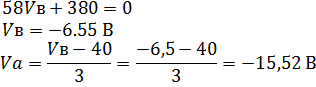
Подставим Vа и Vв в выражения для токов:
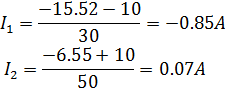
По первому закону Кирхгофа найдем 
:
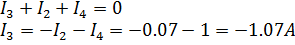
Полученные токи в ветвях:
