A.) По критерию Найквиста;

A.) По критерию Найквиста;

B.) По критерию Гурвица;

C.) По корням характеристического уравнения

Построить переходной процесс для замкнутой импульсной САУ.

Определить статическую и кинетическую ошибки замкнутой импульсной САУ.

Провести сравнение расчетных результатов с данными, полученными на основе пакета прикладных программ.

1 Преобразовать исходную структурную схему к типовому виду; определить непрерывную передаточную функцию приведенной непрерывной части разомкнутой импульсной системы ;

Исходная структурная схема импульсной САУ

Рис 1.

(время запаздывания);

;

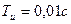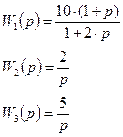
Преобразуем исходную структурную схему к типовому виду:

Преобразованная структурная схема

Рис 2.

Согласно Рис.2, выражение для непрерывной передаточной функции разомкнутой системы будет определяться следующим соотношением:

Т.к. ,

то

Определим весовую функцию для приведенной непрерывной части САУ . Для этого представим в виде суммы слагаемых:

Тогда

2 Нахождение дискретной передаточной функции разомкнутой импульсной системы по ;

Так как по условию расчетного задания в импульсной системе существует небольшое запаздывание (, но не равно нулю), то в выражении для дискретного преобразования Лапласа суммирование начинается не с нулевой дискреты (), а с первой дискреты (). Учитывая этот факт, получим передаточную функцию разомкнутой дискретной системы: где

Также передаточную функцию можно получить следующим способом:

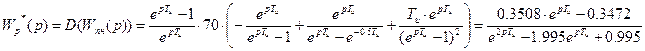
3 Построение годографа разомкнутой импульсной САУ:

a.) По выражению ;

Построим АФХ (годограф) разомкнутой импульсной САУ. Для этого запишем выражение для комплексного коэффициента усиления:

;

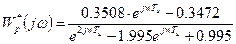Используя формулу Эйлера получим:

Выделим в выражении действительную (Re) и мнимую (Im) части. Для этого необходимо преобразовать знаменатель выражения ; умножить числитель и знаменатель на комплексно–сопряженное знаменателю число; и снова осуществить преобразование.

Значения и , полученные для разных , сведены в таблицу 1, а АФХ рассматриваемой импульсной САУ изображена на Рис.3.

АФХ импульсной САУ

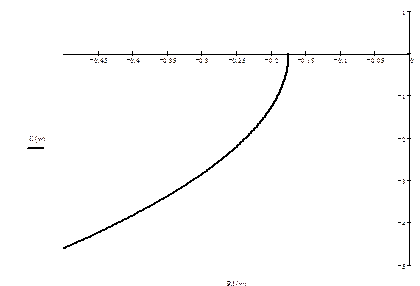
Рис.3.

b.) По годографу

Построение годографа по годографу производится согласно выражению:

В приближении:

где

Таблица 1.

	5⁰	10⁰	20⁰	45⁰	60⁰	90⁰	120⁰	150⁰
Точный метод
	-0,423	-0,237	-0,190	-0,178	-0,176	-0,175	-0,175	-0,175	-0,175
	-4,01	-1,996	-0,990	-0,421	-0,302	-0,174	-0,101	-0,047

Приближённый метод
	-0,404	-0,232	-0,188	-0,172	-0,167	-0,158	-0,15	-0,144	-0,142
	-4,01	-1,993	-0,984	-0,408	-0,287	-0,157	-0,086	-0,038

4 Оценка устойчивости замкнутой импульсной САУ и нахождение предельного коэффициента усиления:

a.) По критерию Найквиста;

Так как АФХ не охватывает точку с координатами (-1,j0),, то рассматриваемая САУ в замкнутом состоянии является устойчивой.

Предельный коэффициент можно определить согласно следующему соотношению:

где – коэффициент усиления разомкнутой САУ; – модуль комплексного коэффициента усиления при его аргументе равном -180⁰.

B.) По критерию Гурвица;

Запишем передаточную функцию дискретной САУ в замкнутом состоянии через Z–преобразование:

Введем подстановку . Тогда характеристическое уравнение принимает вид:

После преобразований, из последнего соотношения получим:

Так как характеристическое уравнение 2-го порядка имеет все положительные коэффициенты, то рассматриваемая система является устойчивой в замкнутом состоянии.

Определим . Для этого передаточную функцию разомкнутой импульсной САУ представим следующим образом:

Тогда соответствующая передаточная функция САУ в замкнутом состоянии примет вид:

Подставим в характеристическое уравнение соответствующее передаточной функции , . Тогда, после преобразований, получим:

Так как для САУ 2-го порядка условие устойчивости сводится к положительности коэффициентов характеристического уравнения, то из последнего уравнения

с.) По корням характеристического уравнения;

Возьмем и для этого коэффициента усиления разомкнутой системы определим устойчивость замкнутой системы на основе корней характеристического уравнения.

Для получим, что:

Откуда корни характеристического уравнения для замкнутой системы равны:

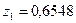т.е. – значит замкнутая САУ является устойчивой.

Предельный коэффициент усиления получаем из решения уравнения:

, откуда и, приравняв получим значение

5 Построение переходного процесса для замкнутой импульсной САУ при К=35

Для этого разделим числитель и знаменатель на .

Тогда

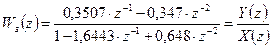
Переходной процесс можно построить по следующему разностному уравнению, полученному из выражения для :

Численные значения переходного процесса в определенные моменты времени замкнутой ИСАУ:

Номер шага	Момент времени	Значения переходного процесса
	0,01	0,351
	0,02	0,581
	0,03	0,732
	0,04	0,831
	0,05	0,896
	0,06	0,939
	0,07	0,967
	0,08	0,985
	0,09	0,997
	0,10	1,005
	0,11	1,01
	0,12	1,013
	0,13	1,015
	0,14	1,017
	0,15	1,018
	0,16	1,019
	0,17	1,02
	0,18	1,021
	0,19	1,022
	0,20	1,023
	0,21	1,024
	0,22	1,025
	0,23	1,026
	0,24	1,027
	0,25	1,028
	0,26	1,029

Вид переходного процесса при К=35