Оптические детали со сферическими поверхностями (линзы, зеркала) являются широко распространенными элементами оптических систем. Качество изображения, даваемого оптическими системами, во многом зависит от того, насколько точно соответствуют расчетным значениям радиусы кривизны сферических поверхностей, полученные при обработке деталей. Поэтому измерение радиусов сферических поверхностей является обязательной и весьма ответственной операцией, как при изготовлении, так и при приеме оптических деталей. Измерение выполняется с относительной погрешностью от 0,05 до 0,2 % от величины радиуса.
Для измерения радиусов кривизны линз используются визуальные и фотоэлектрические сферометры, однако первые имеют низкую производительность и содержат возможность появления грубых ошибок в процессе измерений.
Рассмотрим измерение радиуса кривизны сферической поверхности на кольцевом сферометре.
По способу получения результатов измерений рассматриваемый метод является
косвенными основан на вычислении радиуса кривизны r сферической поверхности 1 (рис. 1а), установленной на опорное кольцо 2 с известным радиусом rк по измеренной с помощью измерительного стержня 3 стрелки прогиба h.
а) б) 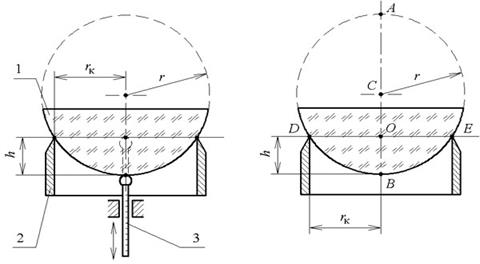
Рис. 1. Принцип работы кольцевого сферометра (а);
к выводу расчетной формулы сферометра (б)
Расчетная формула сферометра может быть выведена на основании рис. 1б.
 . Верно? (2)
. Верно? (2)
При измерении радиусов кривизны полированных поверхностей используют кольца, опорами в которых являются три шарика установленные под углом 120°.
На основании рис. 2 следует рассмотреть влияние радиусов шариков на результаты измерения. Несложно заметить, что при использовании колец с опорными шариками определяется радиус сферы проходящей через центры этих шариков. Следовательно, при вычислении по формуле (2) радиуса кривизны выпуклой измеряемой сферы (рис. 2а) из полученного результата необходимо вычесть значение радиуса опорного шарика, и прибавить его при вычислении радиуса кривизны вогнутой сферической поверхности (рис. 2б). В результате расчетная формула (2) примет вид
 , (3) , (3)
|
где- ρ – для выпуклой сферической поверхности; + ρ – для вогнутой сферической поверхности.
а) б)

Рис. 2. Влияние радиусов шариков опорного кольца на результат измерения:
а) выпуклой поверхности; б) вогнутой поверхности
В формуле (3) величины rк и ρ заранее измеряютс высокой точностью и записывают в аттестат прибора, а величину h измеряют в процессе контроля.
Для ее измерения используются визуальные методы, как, например, в сферометре ИЗС-7 [1] или фотоэлектрические, где отсчеты снимаются с помощью преобразователей линейных перемещений (фотоэлектрический стационарный сферометр ИЗС-11 [2]), схема которого приведена на рис. 3.

Рис. 3. Автоматизированный сферометр:
1 — измерительная пиноль; 2 — кольцо (сменное) с тремя сферическими
опорами (шарами); 3 — проверяемая деталь (пробное стекло); 4-8 — преобразователь линейных перемещений, состоящий из отражающей 4 и прозрачной 5 дифракционных решеток, блока 6 из отклоняющего клина и линз, фотоприемников 7 и светодиода 8; 9 — микропроцессор серии К 580; 10 — привод пиноли
Контроль радиуса сферы R поверяемой линзы производится путем измерения стрелки прогиба y поверхности измерительной пинолью с последующим вычислением величины радиуса микропроцессором по формуле

 , (4)
, (4)
где D — диаметр опорного кольца, rk — радиус сферы опоры — шара (для вогнутой поверхности знак плюс, выпуклой — минус), п — число электрических счетных пульсов, вырабатываемых преобразователем линейных перемещений, А — цена импульса (А = 0,1 мкм).
Технические данные сферометра
Контролируемый радиус, мм:
наименьший.................................................. 10,
наибольший................................................. ∞
Предел измерения стрелки прогиба, мм...........................................±15
Диаметр сменных колец, мм:
наименьший.................................................. 15
наибольший................................................. 120
Максимальная масса контролируемой детали, кг.............................. 3
Диапазон изменения значения измерительного усилия, Н................ 0,5 - 5
Предельное значение погрешности (по результатам испытания
опытного образца), %......................................................................... 0,012
В предлагаемой лабораторной работе представлен макет «накладного» (переносного) сферометра, основанного на базе фотоэлектрического преобразователя линейных перемещений ЛИР 14, изготовленного в СКБ ИС (г. С.-Петербург).
Устройство этого преобразователя приведено на рис. 4.

Рис. 4. Устройство фотоэлектрического преобразователя линейных перемещений ЛИР-14
Основные узлы фотоэлектрического преобразователя линейных перемещений (ПЛП):
-шток 1 с запрессованным на нем ограничителем 2 перемещается в подшипнике качения, наружная обойма 3 которого запрессована в корпусе 4;
растровая шкала 5 в оправе жестко связана через ограничитель со штоком;
- узел считывания в составе индикаторной пластины 6, платы осветителей 7 и платы фотоприемников 8, смонтированных на оправе 9, крепится к корпусу 4 через штифт 10, что позволяет создавать наклон индикаторной пластины относительно шкалы для обеспечения параллельности штрихов их растров.
Шток, ограничитель и шкала образуют подвижный модуль, способный совершать поступательные перемещения относительно индикаторной пластины в пределах хода штока. Параллельно перемещению штока в корпус установлена направляющая 11. Двумя винтами 12 выбирается зазор между ограничителем и направляющей, что исключает разворот подвижного модуля.
Усилие, обеспечивающее постоянный контакт наконечника 13 с поверхностью контролируемого объекта и возврат штока в исходное положение (при любой ориентации ПЛП в пространстве), создается работающей на растяжение цилиндрической пружиной 14. Один конец пружины закреплен на стойке 15 неподвижной части ПЛП, а другой - на ограничителе 2 подвижного модуля.
Со стойкой 15 жестко связан кронштейн 16 с закрепленным на нем нормирующем? преобразователем 17. Через отверстия в кронштейне пропущены провода от плат узла считывания к нормирующему преобразователю.
Кабель 18 обеспечивает питание ПЛП и его связь с устройством приема информации потребителя. В ПЛП моделей ЛИР-15, ЛИР-17 кабель вклеен в отверстие корпуса 4, к которому крепится кожух 19. В ПЛП модели ЛИР-14 положение кабеля фиксируется прижимом 20, что предохраняет распайку кабеля на плате нормирующего преобразователя. Выходящий из ПЛП конец кабеля проходит через ниппель 21, зафиксированный прижимом 22 на крышке 23 кожуха 24.
Принципиальная схема сферометра приведена на рис. 5.

| ? |
Рис. 5. Принципиальная схема сферометра на базе преобразователя ЛИР-14:
1- измерительный оптический растр; 2 - источник излучения;
3 - индикаторный оптический растр; 4 - фотоприёмники; 5 – измерительный шток; 6 –контролируемая линза; 7 – опорные шары; 8,9 - преобразователи сигналов U1 и U2 (усилители и формирователи импульсов); 10 – блок интерполирования; 11 - цифровой дисплей
Линейное перемещение штока 5 преобразуется с помощью измерительного 1 и индикаторного 3 оптических растров в изменение светового потока, падающего на фотоприёмники 4, которые вырабатывают пропорциональные? аналоговые электрические сигналы U1 и U2. Эти сигналы усиливаются, обрабатываются и из них формируются счётные электрические импульсы.
Функция, связывающая перемещение штока с числом n счётных импульсов, имеет вид
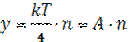 ,
,
где к - коэффициент деления интерполятора, Т - период деления растров, А - цена счетного импульса в линейной мере.
Вычисление радиуса R линзы производится по следующей формуле
,  , (4)
, (4)
, где D - диаметр опорного кольца, rk - радиус сферической опоры-шара (для вогнутой поверхности знак плюс, для выпуклой - минус), у – стрелка прогиба измеряемой линзы, n - число электрических счетных импульсов, вырабатываемых индикатором линейных перемещений, A - цена импульса.
Эта формула приведена выше
Основными погрешностями, влияющими на точность измерений в этом сферометре являются: погрешность диаметра опорного кольца (ΔRΔD), погрешность радиуса сферических опор (ΔRΔ r), контактная деформация линзы и опор, обусловленная весом линзы (Δfл); контактная деформация линзы и сферического наконечника штока под действием мерительного усилия (Δfн); погрешность измерения стрелки прогиба (ΔRΔy); влияние отклонение температуры от номинального значения (ΔRΔT), а так же погрешность измерения радиуса, возникающая из-за смещения штока относительно центра опорного кольца (несоосность) (ΔRΔx).
Эти погрешности оказывают существенное влияние на точность контроля радиусов сферических поверхностей, но могут быть скомпенсированы алгоритмически.
Аттестация сферометра может производиться различными методами, например, измеряя известные радиусы кривизны пробных (эталонных) стекол.
Макет устройства изображен на рис.6.
Сферометр состоит из корпуса, с тремя ножками-опорами 4 в верхней части которого крепится опорное кольцо 3. Это опорное кольцо может быть сменным 6 и в нем закреплены через 120о три опоры-шара 7 для установки и базирования контролируемой линзы. В нижней же части корпуса установлен преобразователь линейных перемещений 3 ЛИР 14, сигналы которого подаются на персональный компьютер 8, где по специальной программе вычисляется по формуле (3) радиус контролируемой линзы.

Рис.6. Внешний вид макета фотоэлектрического сферометра:
1 – эталон плоскости; 2 - опорное кольцо; 3 – фотоэлектрический преобразователь ЛИР-17; 4 – корпус сферометра; 5 – контролируемые линзы; 6 – сменное опорное кольцо; 7 – опоры-шары; 8 – персональный компьютер.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
5.1. Включить в сеть персональный компьютер 8 (рис. 6), дождаться загрузки операционной системы и запустить программу работы со сферометром, кликнув мышкой по пиктограмме с именем «Spherometer». Вид интерфейса программы приведен на рис. 7.
а) б)
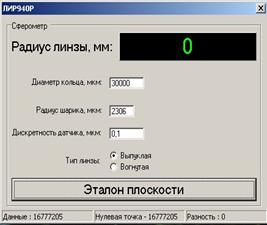

Рис. 7. Вид интерфейса программы:
а) – при нажатой кнопке «Эталон плоскости»; б)- при измерении радиуса кривизны линзы
5.2. Провести измерения радиусов кривизны линз (получить у преподавателя), вначале устанавливая на опорное кольцо 2 (рис.6) эталон плоскости 1 и нажимая соответствующую кнопку, а затем измеряемую линзу. Все измерения выполняются не менее 3-х раз.
5.3. Оценить точность контроля радиусов сферометром, измерив радиус кривизны пробного стекла, имеющегося в составе сферометра.
5.4. По результатам работы составить отчет, который должен содержать следующее: цель работы; сведения о назначении и устройстве сферометра; ПЛП, краткий принцип работы фотоэлектрического преобразователя; результаты измерений.
ВОПРОСЫ ДЛЯ ЗАЩИТЫ
1. Изложить порядок измерения радиуса кривизны отдельной сферической поверхности.
2.Вывести формулу для определения радиуса кривизны сферической поверхности.
3.Определить погрешности, оказывающие большее влияние на результат измерения радиуса кривизны сферической поверхности.
4. Оценить погрешность сферометра из-за влияния погрешности диаметра опорного кольца.
5. Оценить погрешность сферометра из-за влияния погрешности измерения стрелки прогиба.
6. Объяснить устройство сферометра и рассказать принцип его работы.
7. Перечислить основные погрешности рассмотренного устройства.
ЛАБОРАТОРНАЯРАБОТА 7






