С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров - давление, объем или температура - остаются неизменными. Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.
Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами (от греческого слова «изос» - равный). Правда, в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объема. Лишь в лабораторных условиях удается поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс - это идеализированная модель реального процесса, которая только приближенно отражает действительность.
Изотермический процесс. Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим. Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой - термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению состояния идеального газа (10.4) в любом состоянии с неизменной температурой произведение давления газа на его объем остается постоянным:

Для газа данной массы при постоянной температуре произведение давления газа на его объем постоянно.
Этот закон экспериментально был открыт английским ученым Р. Бойлем (1627-1691) и несколько позже французским ученым Э. Мариоттом (1620-1684). Поэтому он носит название закона Бойля - Мариотта.
Закон Бойля - Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха.
Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Зависимость давления газа от объема при постоянной температуре графически изображают кривой, которую называют изотермой. Изотерма газа изображает обратно пропорциональную зависимость между давлением и объемом. Кривую такого рода в математике называют гиперболой (рис.10.1).
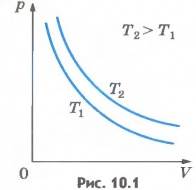
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V =const. Поэтому изотерма, соответствующая более высокой температуре T2, лежит выше изотермы, соответствующей более низкой температуре T1 (см. рис.10.1).
Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость молекул после ударов о поршень увеличивается, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.
Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всем сосуде. Если значения давления и температуры в различных точках объема разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние. Равновесное состояние - это состояние, при котором температура и давление во всех точках объема одинаковы. Параметры состояния газа могут быть определены, если он находится в равновесном состоянии. Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом. Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.
Изобарный процесс. Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным (от греческого слова «барос» - вес).
Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объема газа к его температуре остается постоянным:

Для газа данной массы при постоянном давлении отношение объема к температуре постоянно.
Этот закон был установлен экспериментально в 1802 г. французским ученым Ж. Гей-Люссаком (1778-1850) и носит название закона Гей-Люссака. Согласно уравнению (10.7) объем газа при постоянном давлении пропорционален температуре:

Эта зависимость графически изображается прямой, которая называется изобарой (рис.10.2). Разным давлениям соответствуют разные изобары. С ростом давления объем газа при постоянной температуре согласно закону Бойля - Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению p2, лежит ниже изобары, соответствующей более низкому давлению p1.
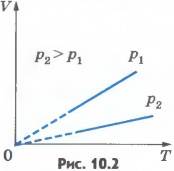
В области низких температур все изобары идеального газа сходятся в точке T =0. Но это не означает, что объем реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объема от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Постоянство давления в цилиндре обеспечивается атмосферным давлением на внешнюю поверхность поршня.
Изохорный процесс. Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным (от греческого слова «хорема» - вместимость).
Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объемом отношение давления газа к его температуре остается постоянным:

Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
Этот газовый закон был установлен в 1787 г. французским физиком Ж.Шарлем (1746-1823) и носит название закона Шарля. Согласно уравнению (10.9) давление газа при постоянном объеме пропорционально температуре:

Эта зависимость изображается прямой, называемой изохорой (рис.10.3). Разным объемам соответствуют разные изохоры. С ростом объема газа при постоянной температуре давление его согласно закону Бойля - Мариотта падает. Поэтому изохора, соответствующая большему объему V2, лежит ниже изохоры, соответствующей меньшему объему V1.
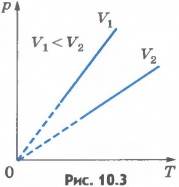
В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке T =0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объема.
Газовые законы - частный случай уравнения состояния идеального газа, один из параметров которого остается постоянным.
| Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). | |||
| Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул. | |||
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.
Мы знаем, что 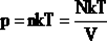 . Следовательно, . Следовательно,  . Учитывая, что . Учитывая, что 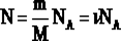 , получим: , получим:  . .
| |||
Произведение постоянных величин есть величина постоянная, следовательно:  - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). - универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
| 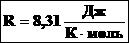
| ||
Таким образом, имеем:
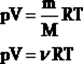 - уравнение состояния (уравнение Менделеева – Клапейрона). - уравнение состояния (уравнение Менделеева – Клапейрона).
| 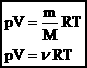
| ||
| Другие формы записи уравнения состояния идеального газа. | |||
1.Уравнение для 1 моля вещества.
Если n=1 моль, то, обозначив объем одного моля Vм, получим: 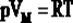 .
Для нормальных условий получим: .
Для нормальных условий получим: 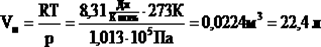
| 
| ||
2. Запись уравнения через плотность: 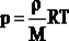 - плотность зависит от температуры и давления! - плотность зависит от температуры и давления!
| 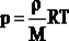
| ||
3. Уравнение Клапейрона.
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: 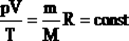
| |||
Эта запись означает, что для данной массы данного газа справедливо равенство: 
| |||
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: 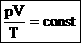 . .
| 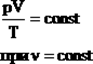
| ||
| Газовые законы. | |||
| 1. Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn; p1=p2=…=pn; T1=T2=…=Tn | |||
Доказательство: 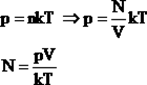 Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
| |||
2. Закон Дальтона.
Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.
Доказать: p=p1+p2+…+pn
Доказательство: 
| |||
| 3. Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения. | |||

Это задача на количество молекул некой порции вещества, и поэтому для её решения существует два пути: решение через количество вещества воды и решение через массу молекулы. Следует отметить, что конечную формулу в обоих случаях мы получим одну и ту же, просто придём к ней с разных сторон.
Наметим себе план решения задачи:
1 Способ:
Для решения задачи первым действием мы найдём количество вещества данной массы воды. И вторым действием, зная, сколько молекул помещается в 1 моле вещества (число Авогадро - 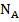 ) и, зная количество молей в нашей порции воды (количество вещества -
) и, зная количество молей в нашей порции воды (количество вещества - 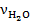 ), мы найдём количество молекул в 120 г воды.
), мы найдём количество молекул в 120 г воды.
2 Способ:
Теперь же первым действием мы найдём массу одной молекулы воды. А вторым действием, зная массу всей порции и массу одной молекулы, найдём опять-таки количество всех молекул.
Независимо от того, каким способом мы решили искать ответ к задаче, нам понадобится молярная масса воды - 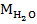 . Она нужна как для нахождения количества вещества:
. Она нужна как для нахождения количества вещества:
 ,
,
так и для нахождения массы одной молекулы
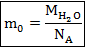
Найдём молярную массу воды. Молярная масса – аддитивная величина, то есть молярная масса сложного вещества – сумма молярных масс химических элементов, входящих в его состав. Не стоит также забывать, что в таблице Менделеева, а именно из нее мы берём значение молярных масс элементов, молярная масса подана в 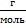 , так что нам нужно ещё перевести ее в СИ, то есть в
, так что нам нужно ещё перевести ее в СИ, то есть в 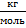 .
.

Теперь, когда мы нашли общую нужную величину для обоих способов решения, получим ответ. И точно также не забудем перевести г в кг, умножая на  .
.

Как и говорилось выше, оба способа решения отличаются лишь тем, как они начинаются. Стоит ещё заметить, что количество молекул, как и любое другое количество, – безразмерная величина.

Прежде чем начинать записывать какие либо формулы, нам нужно уяснить два момента, фигурирующие в условии задачи. Первое – это то, что мы считаем воздух, который является смесью газов, неким псевдогазом с собственными молекулами. И второе – это то, что условие здесь нам подаётся в виде словосочетания «нормальные условия». Значения величин, которые будут нужны нам для подсчётов, мы возьмём из табличных данных: давление при нормальных условиях равно атмосферному давлению и обозначается  , плотность воздуха при нормальных условиях
, плотность воздуха при нормальных условиях 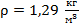 .
.
Эту задачу следует решать, используя основное уравнение МКТ:
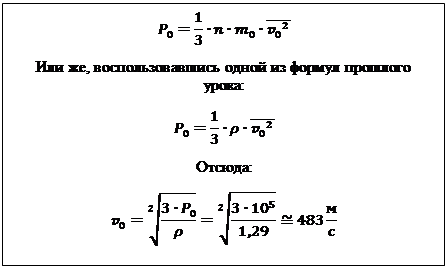
Перейдём к третьей задаче.
Эта задача также является задачей на основное уравнение МКТ, поэтому её решение начинается точно так же, как и решение предыдущей задачи:
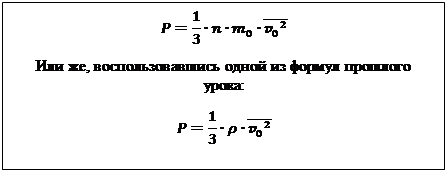
Однако теперь мы столкнулись с дополнительной сложностью, ведь мы не знаем, что за газ находится в сосуде, поэтому не можем воспользоваться табличными данными. Зато мы можем вспомнить определение плотности (масса единицы объёма) и в связи с этим записать

При подстановке данных мы не забыли перевести г в кг, а также л в  , учитывая что
, учитывая что 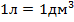 .
.
Домашнее задание:
1. Учить лекционный материал.
2. Ответить на вопросы:
1. Что называют уравнением состояния?
2. Какая форма уравнения состояния содержит больше информации: уравнение Клапейрона или уравнение Менделеева - Клапейрона?
3. Почему газовая постоянная R называется универсальной?
4. Как определяют шкалу температур по Цельсию?
5. Как можно осуществить изотермический, изобарный и изохорный процессы?
6. Какое состояние системы (газа) считается равновесным?
7. Как качественно объяснить газовые законы на основе молекулярно-кинетической теории?






