22.01.2015
Урок 36 (10 класс)
Тема. Относительность одновременности событий
Статья Альберта Эйнштейна «Электродинамика движущихся тел», посвященная СТО, была написана в 1905 году, а в 1907 году автор направил ее на конкурс в университет г. Берна. Один из профессоров вернул Эйнштейну его работу со словами: «Того, что вы написали здесь, я совершенно не понимаю». В 1916 году была написана работа по общей теории относительности. Вряд ли существовал другой такой ученый, личность которого была бы столь популярна среди населения всей планеты и вызывала всеобщий интерес.
С точки зрения СТО продолжительность событий, количество движения, масса тела не являются величинами абсолютными, они зависят от скорости движения наблюдаемых объектов относительно наблюдателя. Эффекты СТО начинают проявляться при скоростях, близких к скорости света, а при обычных, земных скоростях движение и характеристики объектов можно рассчитывать по хорошо знакомым классическим формулам. Теория относительности – дальнейшее обобщение, развитие физических законов движения. Она не отменяет, а включает в себя как необходимую составную часть всю классическую механику.
Рассмотрим некоторые следствия, вытекающие из СТО:
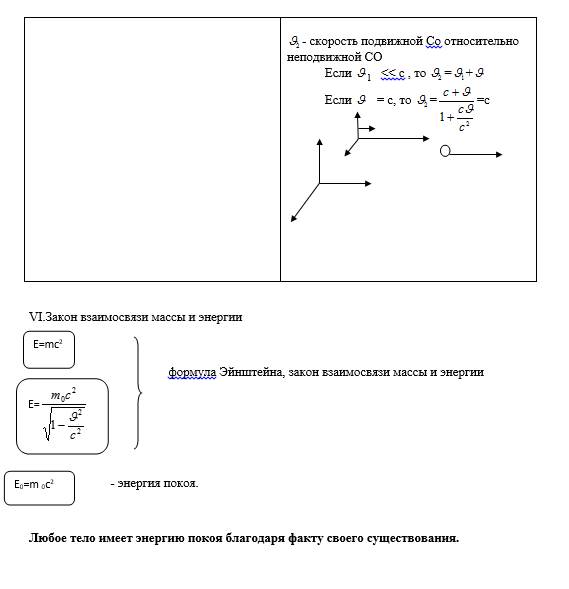
Релятивистский закон сложения скоростей.
Если тело движется со скоростью v в одной системе отсчета, то в другой системе отсчета, относительно которой первая система отсчета движется со скоростью v1 в том же направлении, скорость тела определяется выражением:
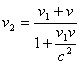
Из этой формулы:
- при v<<c и v1 <<c можно получить классический закон сложения скоростей v2 = v1 +v
Относительность одновременности событий
В механике Ньютона одновременность двух событий абсолютна и не зависит от системы отсчёта. Это значит, что если два события происходят в системе K в моменты времени t и t1, а в системе K’ соответственно в моменты времени t’ и t’1, то поскольку t=t’, промежуток времени между двумя событиями одинаков в обеих системах отсчёта
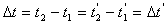
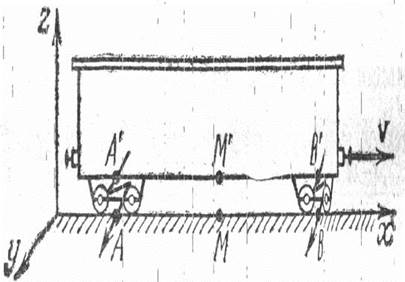
В отличие от классической механики, в специальной теории относительности одновременность двух событий, происходящих в разных точках пространства, относительна: события, одновременные в одной инерциальной системе отсчёта, не одновременны в других инерциальных системах, движущихся относительно первой. На рисунке расположена схема
эксперимента, который это иллюстрирует. Система отсчета K связана с Землёй, система K’ — с вагоном, движущимся относительно Земли прямолинейно и равномерно со скоростью v. На Земле и в вагоне отмечены точки А, М, В и соответственно А’, M’ и В’, причем АМ=МВ и А’M’=M’B’. В момент, когда указанные точки совпадают, в точках А и В происходят события — ударяют две молнии. В системе К сигналы от обоих вспышек придут в точку М одновременно, так как АМ=МВ, и скорость света
одинакова во всех направлениях. В системе К’, связанной с вагоном, сигнал из точки В’ придет в точку M’ раньше, чем из точки А’, ибо скорость света
одинакова во всех направлениях, но М’ движется навстречу сигналу пущенному из точки B’ и удаляется от сигнала, пущенного из точки А’. Значит, события в точках А’ и B’ не одновременны: события в точке B’ произошло раньше, чем в точке A’. Если бы вагон двигался в обратном направлении, то получился бы обратный результат.
|
Понятие одновременности пространственно разделенных событий относительно. Из постулатов теории относительности и существования конечной скорости распространения сигналов следует, что в разных инерциальных системах отсчёта время протекает по-разному.
Преобразования Лоренца
В соответствии с двумя постулатами специальной теории относительности междукоординатами и временем в двух инерциальных системах К и К' существуютотношения, которые называются преобразованиями Лоренца. В простейшем случае, когда система К’ движется относительно системы К соскоростью v так, как показано на рисунке (см ниже), преобразования Лоренцадля координат и времени имеют следующий вид:
, 
, 
, 
,
, 
, 
, 
.
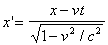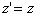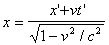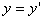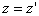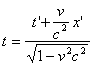Из преобразований Лоренца вытекает тесная связь между пространственными и временными координатами в теории относительности; не только пространственные координаты зависят от времени (как в кинематике), но и время в обеих системах отсчёта зависит от пространственных координат, а также от скорости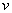 
движения системы отсчёта K’.
Формулы преобразований Лоренца переходят в формулы кинематики при v/c<<1.
В этом случае
, , , 
,
, , , 
.
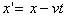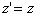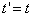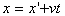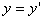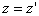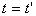Переход формул теории относительности в формулы кинематики при условии v/c<<1 является проверкой справедливости этих формул.
Домашнее задание:
1. Е.В. Коршак, А.И. Ляшенко, В.Ф. Савченко. Физика. 10 класс, «Генеза», 2010. Повторить §37 (с.127-129).
2. Учить лекционный материал.
3. Ответить на вопросы 1-3 устно с.129.
