Элементы линейной алгебры
1. Вычислить определитель квадратной матрицы 
, используя математическую функцию МОПРЕД. Для этого:
· Ввести исходную матрицу (каждый элемент матрицы занести в свою ячейку).
· Установить указатель мыши в свободную ячейку (для результата) и вызвать нужную функцию с помощью Мастера функций.
· В диалоговом окне ввести диапазон значений исходной матрицы.
2. Вычислить обратную матрицу квадратной матрицы, используя математическую функцию МОБР.
Для этого:
· Занести в таблицу исходную матрицу.
· В свободном месте таблицы выделить блок для обратной матрицы (размерность обратной матрицы совпадает с размерностью исходной матрицы).
· Вызвать Мастер функций, выбрать в классе математических и тригонометрических функций требуемую функцию.
· В диалоговом окне функции указать диапазон, в котором находится исходная матрица, нажать «OK». В выделенном под обратную матрицу блоке появится первый элемент вычисленной обратной матрицы.
· Поставить курсор в строку формул, выполнить комбинацию клавиш «Ctrl»+«Shift»+«Enter». В выделенном блоке появится вычисленная обратная матрица.
3. Вычислить произведение матриц 
, используя математическую функцию МУМНОЖ. Для этого выполнить действия аналогично предыдущему пункту.
4. Решить систему линейных уравнений
методом обратной матрицы.
Метод обратной матрицы заключается в следующем: пусть дана система линейных уравнений вида A*X=B, где A - матрица коэффициентов при неизвестных; X - вектор неизвестных; B - вектор свободных членов.
Тогда 
, где 
- обратная матрица матрицы A.
Для решения необходимо выполнить следующее:
· Занести в таблицу исходную матрицу коэффициентов при неизвестных.
· Занести в таблицу столбец свободных членов.
· Вычислить обратную матрицу матрицы коэффициентов при неизвестных.
· Выделить диапазон ячеек для столбца неизвестных.
· Умножить обратную матрицу на столбец свободных членов.
Сделать проверку (умножить исходную матрицу коэффициентов при неизвестных на полученный столбец значений неизвестных).
Работа с процедурой Подбор параметра
Подбор параметра - средство Exce l для анализа таблицы, при котором значения ячейки-параметра изменяются так, чтобы число в целевой ячейке стало равным заданному. С помощью этого средства возможен, например, поиск решения уравнения с одним неизвестным. Решение задачи производится через команду Подбор параметра меню Сервис. В диалоговом окне устанавливается адрес целевой ячейки, ее значение, адрес ячейки параметра.
Программа Подбор параметра доступна только в том случае, если она отмечена в диалоговом окне Надстройки, которое открывается с помощью команды Надстройки меню Сервис.
1. Решить уравнение 
, используя Подбор параметра. Для этого:
· В ячейку А1 ввести текст «х=».
· Ввести начальное значение переменной x в ячейку B1. Т.к. х – неизвестное, то начальное значение можно взять любое (например, ноль).
· В ячейку А3 ввести текст «Левая часть уравнения».
· В ячейку А4 ввести формулу =5*А1^2-2*A1+6.
· В ячейку D3 ввести текст «правая часть уравнения».
· В ячейку D4 ввести число 8.
· В ячейку C4 ввести текст «=».
· Выполнить команду Подбор параметра. Установить:
· адрес целевой ячейки – А4; значение целевой ячейки - 8; изменяя ячейку - B1. Таким образом, процедура Подбор параметра будет автоматически изменять значение в ячейке B1, то есть x, до тех пор, пока значение целевой функции в ячейке A4 не станет равным 8.
2. Решить уравнения, используя процедуру Подбор параметра:
а) 
;
б)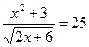 
;
в) 
1. Решить задачу: известен размер вклада, который будет помещен в банк на некоторый срок под определенный процент. Требуется рассчитать сумму возврата вклада в конце периода и определить условия помещения вклада, наиболее подходящие для его владельца.
· Создать таблицу:
Таблица 10. – Вклады
| Размер вклада, руб. | |
| Срок вклада, лет | |
| Процентная ставка | 5% |
| Коэффициент увеличения вклада | |
| Сумма возврата вклада, руб. |
Коэффициент увеличения вклада при начислении сложных процентов вычисляется по формуле: =(1+процентная ставка)^(срок возврата вклада).
Сумма возврата вклада вычисляется по формуле:
=(размер вклада)*(коэффициент увеличения вклада)
· Скопировать таблицу. В копии, используя Подбор параметра, рассчитайте процентную ставку, при которой сумма возврата вклада будет составлять 8000 рублей.
· Скопировать исходную таблицу. В копии, используя Подбор параметра, рассчитайте срок вклада, при котором сумма возврата вклада будет составлять 8000 рублей.
