ПРАКТИЧЕСКАЯ РАБОТА № 25
По дисциплине: МАТЕМАТИКА
Наименование работы: РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПРИ ПОМОЩИ ФОРМУЛ ЭЙЛЕРА.
Для специальностей 210705, 210709, 210723.
Составлена преподавателем Калмыковой О. И.
г. Смоленск
2011 г.
Практическая работа № 25.
для студентов 2 курса.
Вариант 1.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
 . .
| Вариант 2.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
 . .
|
Вариант 3.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
 . .
| Вариант 4.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
 . .
|
Вариант 5.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
 . .
| Вариант 6.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.

|
Вариант 7.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.

| Вариант 8.
Методом Эйлера постройте таблицу значений для заданного дифференциального уравнения с начальным условием y(0)=1. В таблице укажите значение решения на отрезке [0, 1] с шагом 0,1. По таблице постройте график решения.
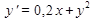
|
6. Порядок выполнения работы:
1.Требование к ТБ;
2. Ответьте на вопросы допуска к работе;
3. Выполните задание, соответствующее варианту.
4. Оформите отчёт;
5. Ответьте на контрольные вопросы.
7. Содержание отчёта:
1. Наименование и цель работы;
2. Результаты выполнения работы;
3. Анализ результатов и выводы.
4. Ответы на контрольные вопросы.
Контрольные вопросы.
1. Понятие дифференциального уравнения.
2. Алгоритм решения дифференциальных уравнений при помощи формул Эйлера.
Методические указания.
Приближенное решение дифференциальных уравнений
Рассмотрим приближенное решение задачи Коши:
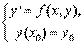 (1)
(1)
на отрезке  , полученное при помощи метода Эйлера. Для этого разобьем отрезок точками
, полученное при помощи метода Эйлера. Для этого разобьем отрезок точками  на
на  равных частей. Пусть
равных частей. Пусть  – длина каждого из полученных отрезков, тогда
– длина каждого из полученных отрезков, тогда  ,
,  . Приближенно найдем значения функции
. Приближенно найдем значения функции  в узловых точках,
в узловых точках,  .
.
Метод Эйлера основан на том, что из определения производной следует приближенное равенство:  , следовательно, дифференциальное уравнение
, следовательно, дифференциальное уравнение  можно заменить разностным уравнением:
можно заменить разностным уравнением:  , которое иначе записывается в виде
, которое иначе записывается в виде
 ,
,
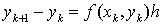 ,
,
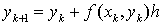 ,
,  . (2)
. (2)
Применяя формулу (2), можно вычислить сначала  по известным значениям
по известным значениям  и
и  , затем вычислить
, затем вычислить  и т.д.
и т.д.
С геометрической точки зрения, при вычислении по формуле (2) на каждом элементарном участке  график решения заменяется отрезком прямой с угловым коэффициентом
график решения заменяется отрезком прямой с угловым коэффициентом  . В результате получается ломаная, которая называется ломаной Эйлера.
. В результате получается ломаная, которая называется ломаной Эйлера.
Пример. Методом Эйлера для уравнения  найти
найти  , если
, если  ; выбрать
; выбрать  . Для расчетов по формуле (2) составим таблицу.
. Для расчетов по формуле (2) составим таблицу.

| 
| 
| 
|
| 0,1 | 1+0=1 | 0,020 | |
| 0,2 | 1+0,020=1,020 | 0,041 | |
| 0,3 | 1,020+0,041=1,061 | 0,064 | |
| 0,4 | 1,061+0,064=1,125 | 0,090 | |
| 0,5 | 1,125+0,090=1,215 | 0,121 | |
| 0,6 | 1,215+0,121=1,336 | 0,160 | |
| 0,7 | 1,336+0,160=1,496 | 0,209 | |
| 0,8 | 1,496+0,209=1,705 | 0,273 | |
| 0,9 | 1,705+0,273=1,978 | 0,357 | |
| 1,0 | 1,978+0,357=2,335 |
Итак,  . Найдем точное решение задачи и сравним полученные результаты:
. Найдем точное решение задачи и сравним полученные результаты:


решение задачи – функция  , получаем
, получаем  . Как видим, погрешность вычисления 2,718–2,335=0,383 довольно велика, но уменьшение величины
. Как видим, погрешность вычисления 2,718–2,335=0,383 довольно велика, но уменьшение величины  позволяет добиться лучших результатов.
позволяет добиться лучших результатов.
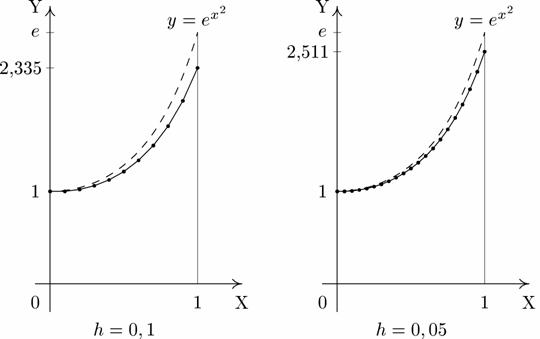
Для сравнения изобразим интегральную кривую и ломаные Эйлера для  и
и  (для наглядности выбраны разные масштабы по координатным осям).
(для наглядности выбраны разные масштабы по координатным осям).