Обработка данных при прямых измерениях с однократными наблюдениями

Современные методы обработки результатов наблюдений

При измерениях

При обработке результатов наблюдений, прежде всего, исполь­зуют основные уравнения измерений вида (1.1 – 1.4):

Прямые измерения Q=сХ, (1.1)

где с - заданный коэффициент.

Косвенные Величина Q является из­вестной функцией от непосредственно измеряемых аргументов Х₁, Х₂, …, Х_m: Q =f(Х₁, Х₂, …, Х_m) (1.2)

При совместных измерениях находят функциональную зависи­мость Y=f(X) между (переменными) физическими величинами X и Y, путем измерений ряда значений Х₁, …, Х_m и соответству­ющих им величин Y₁, …, Y_m:

Y_i=f(X_i) (1.3)

При совокупных измерениях значения набора одноименных ве­личин Q₁, …, Q_m находят, как правило, путем измерений сумм или разностей этих величин в различных сочетаниях. Уравнения измерений имеют вид:

(1.4)

где коэффициенты с_ij принимают значения ±1 или 0.

 

Однако, если попытаться непосредственно подставить полученные эксперимен­тальные данные в эти уравнения, то получится несовместная сис­тема. Это обусловлено тем, что уравнения измерений связывают истинные значения величин, а полученные результаты наблюдений неизбежно содержат погрешности. Поэтому для нахождения иско­мого результата измерения уравнения (1.1 -1.4) необходимо допол­нить выражениями для результатов наблюдений.

Например, при прямых измерениях с многократными наблюде­ниями (когда Q=X) результаты наблюдений х_1, …, х_n можно представить в виде:

х_i=Q+ζ(x_i), i=1…n, (1)

где ζ(x_i) - погрешности наблюдений.

По этим данным необходимо найти приближенное значение , близкое к истинному значению Q, и оценить его погрешность ζ()= -Q. В зависимости от предположений относительно пог­решностей и критерия качества оценки, могут быть использо­ваны различные оценки . В частности, если погрешности наблю­дений ζ(x_i) являются случайными, то задача сводится к классиче­ской задаче статистики — оценить среднее значение Q по выборке х₁, …, х_n вида (1). Как правило, присутствуют также системати­ческие погрешности, которые необходимо учитывать и оценивать.

Отметим, что из полученной системы (1) необходимо найти только результат измерения и оценить характеристики (напри­мер, СКО) его погрешности.

Аналогично формируются системы уравнений для других кате­горий измерений. При косвенных измерениях уравнение (1.2) следует дополнить выражениями для результатов наблюдений аргументов:

x_i=X_i+ζ(x_i) (2)

y_i=Y_i+ζ(y_i) (3)

При совокупных или совместных измерениях — к уравнениям (1.3) или (1.4) добавляют соотношения (3). Если также измеряют значе­ния X_i, то добавляют соотношения (2).

После того, как сформирована система уравнений, для опреде­ления результата измерения может быть использовано несколько алгоритмов вычислений, в зависимости от предположений относительно погрешностей наблюдений и критерия качества оценки . Алгоритм обработки данных представляет собой последователь­ность алгебраических и логических операций, в результате приме­нения которых к экспериментальным данным x_i, y_i,… будет по­лучен искомый результат измерения и характеристики его по­грешности.

Многочисленные и разнообразные алгоритмы обработки данных можно разделить на группы по нескольким признакам. Прежде всего, по виду исходной системы уравнений они делятся на группы, соответствующие прямым, косвенным, совместным и совокупным измерениям. Математическую основу для них составляют различ­ные статистические методы. В частности, при прямых измерениях используют методы оценивания среднего значения по выборке, а при косвенных — кроме того, методы приближения функций. При совместных и совокупных измерениях используют, прежде всего, метод наименьших квадратов.

Методы обработки данных также можно разделить согласно видам моделей, используемых для описания погрешностей. Наибо­лее многочисленными являются статистические методы, основан­ные на моделях погрешностей как случайных величин. Среди ста­тистических методов, в свою очередь, выделяются классические параметрические методы, непараметрические методы и современ­ные устойчивые методы.

Важным признаком классификации методов обработки является также критерий качества оценки и способ его использования при построении алгоритма. Прежде всего, выделяются методы, ко­торые оптимальны согласно определенному критерию в рамках точной математической модели данных. Однако для них требуется значительная априорная информация; например, что случайные погрешности имеют гауссовское распределение. Типичными являются алгоритм усреднения данных и метод наименьших квадратов. Если погрешности результатов наблюдений имеют гауссовские распределения, то эти методы являются оптимальными: первый - для прямых, второй - для совместных измерений. Их можно использовать и в более широком круге задач, не вводя требования гауссовского распределения. При этом они весьма удобны в вычислительном плане, хотя и не всегда высоко эффективны. К сожалению, формальное отбрасывание ограничений в оптимальном методе часто приводит к неустойчивости, мало эффективному методу. Целесообразно так модифицировать оптимальный метод, чтобы он оставался эффективным для широкого круга случаев; именно это достигается в современных устойчивых (робастных) методах.

Наконец, обширную группу образуют так называемые эвристи­ческие методы, которые не имеют формального обоснования. Обыч­но они просты и устойчивы по отношению к помехам и отклонениям от моделей; поэтому их часто используют на начальном этапе обработки, чтобы получить исходные приближения для примене­ния более сложных и точных методов. Однако они менее точны и для них труднее оценивать точность получаемых результатов.

Кроме статистических методов, при обработке данных исполь­зуют численные методы, необходимые для преоб­разований исходных соотношений, а также для численной реали­зации статистических методов.

 

Обработка данных при прямых измерениях с однократными наблюдениями

 

Прямые измерения с однократными наблюдениями являются наиболее распространенными на производстве и в научных иссле­дованиях. Если выполняется одно только наблюдение, то за ре­зультат измерения принимают единственное полученное значение. С целью дополнительного контроля отсутствия промахов и грубых погрешностей часто выполняют 2—3 наблюдения; тогда за резуль­тат измерения принимают среднее арифметическое их результатов. Таким образом, получение результата измерения в этом случае очевидно.

Обработка данных сводится, главным образом, к оцениванию погрешности измерения на основе априорной информации, роль ко­торой в этом случае особенно велика. Она существенно различается для трех групп измерений в соответствии со степенью полноты априорной информации.

Изложим более подробно оценивание погрешностей технических измерений. При этом погрешности оценивают априорно на основе нормативных данных о свойствах используемых средств измерений и с учетом возможных значений влияющих величин; для этого не­обходимо также определить диапазон возможных значений изме­ряемой величины.

Погрешность измерения представляется в виде суммы состав­ляющих (ζ(Q)= ζ_м + ζ_и + ζ_{л, (1.7)}

где ζ_м — методическая погрешность, ζ_и — инструментальная погреш­ность, ζ_л — личная погрешность); при этом каждая из них может содержать система­тические и случайные составляющие. Инструментальная погреш­ность ζ_и складывается из основных ζ_0i и дополнительных ζ_ij погрешностей используемых средств измерений (i=l,..., n — номера средств измерений, j — номера влияющих величин).

Характеристики основных погрешностей содержатся в техниче­ской документации на средства измерений. Дополнительные по­грешности оценивают на основе характеристик, приведенных в до­кументации, и заданных диапазонов возможных значений влия­ющих величин.

Кроме того, при выполнении измерений в динамическом режиме необходимо учитывать также динамические погрешности. Для их оценивания необходимо знать динамические характеристики средств измерений (которые должны быть указаны в технической документации), а также свойства (в простейшем случае — частот­ные) входных сигналов.

Анализ и оценивание методической погрешности ζ_м выполняется при разработке методики выполнения измерения.

После того, как получены границы для отдельных составля­ющих, необходимо выполнить их суммирование и найти границы общей погрешности.

Подчеркнем, что при априорном оценивании приходится рас­считывать погрешность в наименее благоприятной точке диапазона возможных значений измеряемой величины. При этом, если есть информация о возможном распределении измеряемых величин, можно ее использовать чтобы дать не столь завышенную оценку погрешности.

Наиболее тщательно, очевидно, выполняют оценивание погреш­ности при апостериорном оценивании с учетом индивидуальных свойств средств измерений и значений влияющих величин. Данный случай выделяется тем, что можно вычислить поправки на некоторые систематические погрешности и внести их в результат измерения (тем самым, повысив точность результата измерения). Здесь также используется исходное разложение (1.7); поэтому вносимая поправка имеет вид:

где - оценки систематических составляющих;

После введения поправки погрешность исправленного резуль­тата =х+с имеет вид

ξ= ξ_М + ξ_И + ξ_Л (8)

где ξ_М = ζ_М - ΰ_М - обусловлена неточностью оценивания методиче­ской погрешности; - обусловлена погрешностью поверки (аттестации) средства измерений, случайной составляющей основ­ной погрешности средства измерений, неточностью определения функций влияния и погрешностями измерений влияющих величин;

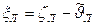- обусловлена неточностью оценивания личной по­грешности.

В выражении (8) каждое слагаемое состоит из ряда составля­ющих, при этом систематические составляющие обычно характе­ризуют границами, а случайные - СКО. В итоге основная задача сводится к суммированию составляющих и нахождению границ погрешности (8).

Измерения с приближенным апостериорным оцениванием по­грешностей составляют, в некотором смысле, промежуточную груп­пу в отношении оценивания погрешностей. Обработку данных вы­полняют на основе априорных сведений об условиях измерений и методических погрешностях, а также взятых из документации сведений о метрологических характеристиках средств измерений. Кроме того, иногда приближенно оценивают (но не измеряют) наиболее существенные влияющие величины. Отметим, что в данном случае нельзя внести поправку в результат измерения; можно лишь оценить его погрешность. Однако при апостериорном оценивании все же известен результат измерения, а также более определенные границы значений влияющих величин, поэтому можно получить уточненные оценки погрешностей (по сравнению с априорным оцениванием).

Пример. Выполнено однократное измерение напряжения U на участке электрической цепи сопротивлением R=(10±0,1) Ом с помощью вольтметра класса 0,5 по ГОСТ 8711—78 (верхний пре­дел диапазона 1,5 В, приведенная погрешность 0,5%). Показание вольтметра 0,975 В. Измерение выполнено при температуре при­мерно 25° С, при возможном магнитном поле, имеющем напряжен­ность до 300 А/м.

Методическая погрешность измерения определяется соотноше­нием между сопротивлением участка цепи R и сопротивлением вольтметра R_V = 900 Ом (которое известно с погрешностью 1%). Показание вольтметра свидетельствует о падении напряжения на вольтметре, определяемом как

U_V= UR_V / (R + R_V) ≈ 0,975 В;

поэтому методическая погрешность здесь равна

ζ_М = U_V - U = - UR/(R + R_V)≈ 0,011B

После введения поправки получим:

0,975+0,011 = 0,986 В.

Неисключенная методическая погрешность (т. е. погрешность опре­деления поправки) определяется погрешностями измерений сопро­тивлений цепи и вольтметра, которые имеют границы 1%. Поэтому погрешность поправки оценивается границами 0,04%, т. е. прене­брежимо мала.

Инструментальная составляющая погрешности определяется ос­новной и дополнительной погрешностями. Основная погрешность оценивается по приведенной погрешности и результату измерения:

Дополнительная погрешность от влияния магнитного поля ле­жит в границах θ_н=±0,5%. Дополнительная температурная по­грешность, обусловленная отклонением температуры на 5°С (от нормальной 20°С), лежит в границах θ_Т=±0,5%. Доверительные границы инструментальной погрешности (при Р=0,95) находят по формуле θ_о .

В абсо­лютной форме граница θ = 0,011 В. После округления результат принимает вид: U = (0,99±0,01) В; Р = 0,95.