Или в виде формулы для первого акционера: D3=C$8*B3–C3.
| A | B | C | D | E | F | G | |
| Коэф. | оплаты: | воскр.: | суббота: | 1,5 | |||
| ТАБЕЛЬ И ЗАРПЛАТА | |||||||
| Дата | День недели | Петр | Иван | Олег | Всего часов | Всего с коэфф. | |
| 10р/ч | 8р/ч | 6р/ч | |||||
| 1.окт | Вт | 9ч | 9ч | 9ч | |||
| 2.окт | Ср | 8ч | 2ч | 8ч | 18ч | 18ч | |
| 3.окт | Чт | ||||||
| 4.окт | Пт | 5ч | 6ч | 8ч | 19ч | 19ч | |
| 5.окт | Сб | 2ч | 10ч | 12ч | 18ч | ||
| 6.окт | Вс | 9ч | 5ч | 8ч | 22ч | 44ч | |
| 7.окт | Пн | 8ч | 6ч | 14ч | 14ч | ||
| 8.окт | Вт | 9ч | 7ч | 16ч | 16ч | ||
| Всего часов: | 41ч | 45ч | 24ч | 110ч | 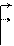 138ч 138ч
| ||
| Часов с коэф.: | 51ч | 55ч | 32ч | 138ч | |||
| Зарплата: | 510р | 440р | 192р | 1142р | |||
| Рис. | 5.7а | дол | жно с | овпасть |
В таблице некоторые значения получились со знаком минус (т.е. акционер, ранее внесший деньги, получит часть их обратно), другие – со знаком плюс (акционер заплатит деньги). Видим, что сумма всех последующих взносов (D8=СУММ(D3:D7)) равна нулю, т.е. наблюдается баланс выплат. Еще раз убедиться в правильности вычислений можно, определив процент окончательных взносов (столбец Е)
=(внесено_сразу+внесено_потом)/внесено_всего.
Или для первого акционера: E3=(C3+D3)/C$8. Видим, что относительные размеры окончательных выплат совпали с размерами относительной собственности каждого из акционеров.
Пример 5.7. Ведение табельной ведомости. Создать таблицу табельной ведомости (документа, фиксирующего число отработанных часов) работников подразделения с расчетом их ежедневной и месячной заработной платы. Считаем, что здесь принята почасовая оплата труда, а рабочий график индивидуальный. Тарифная часовая ставка оплаты установлена своя для каждого работника (ячейки С4, D4, E4). Кроме того, установлена повышенная оплата труда в субботние (с коэффициентом 1,5) и воскресные (с коэффициентом 2) дни. В будний день коэффициент считается равным 1. Пусть, нужно создать таблицу за октябрь месяц. Для быстрого ввода дат месяца воспользуемся механизмом автозаполнения. Внесем в клетку А5 значение 1.окт, а затем мышью скопируем его вниз до конца месяца. Excel расставит нужные последовательные даты месяца автоматически. В столбец День недели введем выражение,
формирующее название дня недели B5= ВЫБОР(ДЕНЬНЕД(A5;2);"Пн";"Вт";"Ср";"Чт";"Пт";"Сб";"Вс"), где номер дня недели (ДЕНЬНЕД(A5;2)) замещается на его имя Пн, Вт и т.д.
В столбце Всего часов определяется сумма астрономических рабочих часов сотрудника (F5=СУММ(C5:E5)) за день, а в столбце Всего с коэффициентом – число часов с учетом увеличивающих коэффициентов за работу в выходные дни (G5=ЕСЛИ(B5="Вс";D$1;ЕСЛИ(B5="Сб";F$1;1))*F5). Таким образом, увеличение оплаты за работу в выходные дни трансформируется в увеличение отработанных часов при их обычной оплате. В итоговой строке 35 введены очевидные формулы суммирования отработанных часов вида С35=СУММ(C5:C34).
В строке 36 – находятся эквивалентные рабочие часы каждого из сотрудников в зависимости от тарифной ставки и работы в выходные
часы_с_коэфф.=общее_число_часов+
воскресных_часов*разность_между_к-том_воскресенья_и_будним_днем+
субботних_часов*разность_между_к-том_субботы_и_будним_днем.
Так, Петром отработано 45 час, а с учетом выходных: 41час+9час(2–1)+2час(1,5–1)=51час.
Или в виде формулы:
C36=C35+СУММЕСЛИ($B5:$B34;"Вс";C5:C34)*($D1–1)+СУММЕСЛИ($B5:$B34;"Сб";C5:C34)*($F1–1).
В строке 37 вычисляется заработок
зарплата=тарифная_ставка * часы_с_коэффициентом.
Отсюда его зарплата (55час*10руб/час=510руб): C37=C$4*C6.
Все Часы с коэфф. для всех работников просуммированы в клетке G36. Видим, что эта сумма (138 час.) совпала с вертикальной суммой, полученной в G35, что показывает правильность расчета эквивалентных часов. Вообще, если имеется какая-либо возможность альтернативного вычисления тех же самых величин, следует это сделать чтобы проверить правильность построения таблицы.
| A | B | C | D | E | F | G | ||
| Коэф. оплаты: | Воскр.: | Суббота: | 1,5 | |||||
| ТАБЕЛЬ И ЗАРПЛАТА | ||||||||
| Дата | День недели | Петр | Олег | Всего часов | Всего с коэфф. | |||
| 10р/ч | 6р/ч | |||||||
| 1.окт | =ВЫБОР(ДЕНЬНЕД (A5;2);"Пн";"Вт";"Ср";"Чт";"Пт";"Сб";"Вс") | 2ч | 10ч | =СУММ (C5:E5) | =ЕСЛИ(B5="Вс"; D$1;ЕСЛИ(B5= "Сб";F$1;1))*F5 | |||
| 8.окт | =ВЫБОР(ДЕНЬНЕД (A12;2);"Пн";"Вт";"Ср";"Чт";"Пт";"Сб";"Вс") | 9ч | 7ч | =СУММ (C12:E12) | =ЕСЛИ(B12="Вс"; D$1;ЕСЛИ(B12= "Сб";F$1;1))*F12 | |||
| Всего часов: | =СУММ(C5:C34) | =СУММ(E5:E34) | =СУММ (F5:F34) | =СУММ(G5:G34) | ||||
| Часов с коэфф.: | =C35+СУММЕСЛИ($B5: $B34;"Вс";C5:C34)*($D1-1) +СУММЕСЛИ($B5:$B34; “Сб”;C5:C34)*($F1-1) | =E35+СУММЕСЛИ($B5: :$B34;"Вс";E5:E34)*($D1-1) +СУММЕСЛИ($B5:$B34; "Сб";E5:E34)*($F1-1) | =СУММ(C36:E36) | |||||
| Зарплата: | =C36*C$4 | =E36*E$4 | =СУММ( C37:E37) | Рис. 5.7б | ||||
К оформлению. Для ячеек С4:Е4 установлен пользовательский формат вида 0,0"р/ч", а для колонок F и G – формат [>0]#"ч";#. На рисунке табель показан по текущий день месяца (например, по 8 октября). Остальные пустые пока строки скрыты, с тем, чтобы не отвлекать внимание пользователя.
 Пример 5.8. Расчеты с вкладчиками банка. Построить таблицу вычисления годовой премии вкладчику банка. Здесь возможно несколько подходов:
Пример 5.8. Расчеты с вкладчиками банка. Построить таблицу вычисления годовой премии вкладчику банка. Здесь возможно несколько подходов:
1. Абсолютный размер премии исчисляется исходя из остатка на счету к концу года. Это самый простой и самый несправедливый способ. Если вкладчик 30 декабря снял крупную (или даже всю) сумму со счета, он получит маленькую премию (или не получит ничего) несмотря на то, что банк пользовался его деньгами весь год (пострадает клиент). Наоборот, если сумма была внесена на счет только 30 декабря, вкладчик получит большую премию за один день хранения, несмотря на то, что ранее на счету, возможно, не было ничего (пострадает банк). Учитывая, что в банке много клиентов, такие потери и приобретения банка, вероятнее всего будут взаимно скомпенсированы, однако этого не скажешь об отдельном вкладчике, особенно, если он понесет финансовый ущерб.
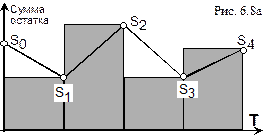
2. Премия исчисляется на основе значений остатков (S1, S2, S3, S4) на счету в каждом из четырех кварталов года. Здесь мы исходим из предположения, что в течение всего квартала на счету находилась именно эта величина. Это, конечно, не так, но лучше чем предыдущий подход. Тогда средний годовой остаток вычисляется как сумма всех этих остатков, деленная на число кварталов (S1+S2+S3+S4)/4. На рис. 5.8а искомое значение пропорционально сумме площадей прямоугольников с высотой Si. (закрашены), которую легко вычислить. Назовем поэтому этот метод методом прямоугольников. Ясно, что он имеет значительные погрешности, которые будут уменьшаться с уменьшением элементарных периодов расчета, например, до двух или одного месяцев и меньше.
3. Более точным будет исчисление среднего годового остатка как суммы среднеквартальных остатков (площадь под ломаной линией на рисунке), деленной на четыре.
средний_вклад_за_год=(ср._остаток_1_кв.+ср._остаток_2кв+ср._остаток 3кв+ср._остаток 4кв)/4
или [(S0+S1)/2+(S1+S2)/2+(S2+S3)/2+(S3+S4)/2]/4=[S0+S4+2(S1+S2+S3)]/8.
Назовем этот метод методом трапеций. В таблице на рис. 5.8б сделаны вычисления значения премий методами прямоугольников и трапеций. Для первого вкладчика это следующие формулы
G5=СУММ(C5:F5)/4*D$1, H5=(B5+F5+2*(C5+D5+E5))/8*D$1.
| A | B | C | D | E | F | G | H | G | H | ||
| Проце | нт прем | ии | 10% | ||||||||
| СЧЕТА КЛИЕНТОВ | |||||||||||
| Номер | Начало | Остатки по кварталам | Премия | Премия | Премия | Премия | |||||
| счета | года | I | II | III | IV | (прямоуг.) | (трапеции) | (прямоуг.) | (трапеции) | ||
| Счет1 | 9,0 | 6,50 | =СУММ(C5:F5)/4*D$1 | =(B5+F5+2*(C5+D5+E5))/8*D$1 | |||||||
| Счет2 | 5,5 | 6,25 | =СУММ(C6:F6)/4*D$1 | =(B6+F6+2*(C6+D6+E6))/8*D$1 | |||||||
| Счет3 | 18,8 | 21,88 | =СУММ(C7:F7)/4*D$1 | =(B7+F7+2*(C7+D7+E7))/8*D$1 | |||||||
| Сумма | 33,3 | 34,63 | =СУММ(G7:G7) | =СУММ(H7:H7) |
Рис. 5.8б
Заметим, что задача нахождения среднего вклада является задачей вычисления определенного интеграла в заданных пределах, и здесь фактически использованы известные методы ее решения (метод прямоугольников и метод трапеций).
4. Все перечисленные методы являются приближенными, поскольку предполагают довольно грубые допущения в отношении сумм на счетах в течение некоторого периода. Как уже указывалось, более точным будет подсчет среднего значения не по кварталам, а по меньшим периодам, но абсолютно точным был бы учет фактического времени нахождения средств клиента на счетах в каждый момент времени. Этот механизм может быть реализован только с привлечением средств программирования (языка VBA), имеющихся в Excel.
Пример 5.9. Продуктовый расчет. При планировании производственной программы, например, в пищевой промышленности, необходимо иметь полное представление об ожидаемых абсолютных потерях и объемном/весовом количестве продукта на каждом этапе обработки. Поскольку все пищевое производство (виноделие, консервирование, хлебобулочная промышленность) является многоступенчатым, контроль за этими параметрами здесь чрезвычайно актуален и осуществляется с помощью так называемого продуктового расчета.

|
|
|
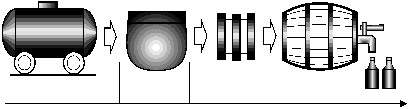
На рис. 5.9а, например, изображена типовая технологическая цепочка обработки виноматериалов. Относительные нормативные потери на каждом из этапов обработки известны из опытных данных и заданы директивно. Обозначим (рис. 5.9б): Пвх – количество продукта на входе всего процесса или его отдельного этапа, Пвых – количество продукта на выходе, К – коэффициент потерь на этапе обработки, D – объем потерь на этапе обработки в абсолютном исчислении. Отсюда можем записать рабочие формулы для каждого этапаПвых=Пвх– D, где D =К·Пвх.
Задача может быть поставлена как прямая (известен объем сырья, нужно найти объем продукта), так и как обратная (известен объем продукта, найти объем потребного для него сырья).
Прямая задача. Заданы: исходное количество продукта (сырья) на входе процесса к началу обработки Пвх, количество этапов обработки N и коэффициенты нормативных потерь на каждом i-ом этапе – Кi от поступившего на данный вид обработки объема продукта. Вычислить абсолютные величины потерь на каждом этапе обработки Di и итоговый выход продукта Пвых.
Обратная задача. Задано потребное количество готового продукта Пвых. Вычислить абсолютные величины потерь на каждом этапе обработки D i и необходимое количество исходного продукта Пвх.
Рабочие формулы для каждого этапа обратной задачи: D =Пвых·К/(1–К) и Пвх=Пвых+ D.
На основании простых рассуждений можно записать итоговые формулы расчета конечного/начального (Пвых/Пвх) продукта для прямой/обратной задачи для всего процесса в целом
Пвых=Пвх(1–К1)(1–К2)... (1–КN), Пвх=Пвых/((1–К1) (1–К2)... (1–КN)).
Решение задачи прямого продуктового расчета приведено в верхней части рис. 5.9в, а формулы рабочего листа на рис. 5.9г. Исходное количество сырья для наглядности взято равным 100. При трехэтапной обработке с относительными потерями в 0,05, 0,11 и 0,02 итоговый выход продукта составит 82,859.
Решение обратной задачи изображено на тех же рисунках в их нижней половине. В качестве выхода технологического процесса взято значение, ранее найденное в прямой задаче (82,859). Как видим, в результате расчетов для обратной задачи получено число 100, т.е. вычисления выполнены верно.
Если вспомнить задачу 5.2, можно заметить, что прямой продуктовый расчет очень похож на задачу определения вклада для сложных процентов. Только там происходит наращивание вклада, а здесь уменьшение продукта. Это обстоятельство можно учесть, изменив на минус знаки при всех коэффициентах потерь. Тогда объем продукта на выходе получим воспользовавшись функцией
=БЗРАСПИС(C2;{–0,05;–0,11;–0,02}) =82,859 или (введя выражение как массив) {=БЗРАСПИС(C2;–B4:B6)} =82,859.
Пример 5.10. Продуктовый расчет с дополнительным сырьем.
Продуктовый расчет, выполненный выше, предполагает, что перерабатывается только исходный продукт. На практике, часто в технологическом процессе предусмотрено внесение (или изъятие) на разных его этапах дополнительных компонентов. Объем вносимого элемента зависит от объема продукта, поступающего на обработку. Решим такую задачу. В таблицу продуктового расчета внесем новый столбец Дополнительное сырье, где разместим коэффициенты (проценты), связывающие объем дополнительного материала с объемом исходного для данного этапа.
Для первого этапа в таблице сформируем выражения:
объем_потерь=коэффициент_потерь*(исходный_объем+дополнительный_объем).
Для любого следующего этапа
объем_на_выходе=исходный_объем+дополнительное_сырье–объем_потерь.
Или в форме клеточных функций: D4=C4*(C2+C2*B4)=C4*C2*(1+B4), E4=C2+C2*B4–D4=C2*(1+B4)–D4.
| A | B | C | D | |
| ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача) | ||||
| Объем сырья: | ||||
| Этап | Коэфф. потерь | Объем потерь | Объем продукта на выходе | |
| 0,05 | 5,000 | 95,000 | ||
| 0,11 | 10,450 | 84,550 | ||
| 0,02 | 1,691 | 82,859 | ||
| ПРОДУКТОВЫЙ РАСЧЕТ (обратная задача) | ||||
| Объем продукта: | 82,859 | |||
| Этап | Коэфф. потерь | Объем потерь | Объем продукта на входе | |
| 0,02 | 1,691 | 84,550 | ||
| 0,11 | 10,450 | 95,000 | ||
| 0,05 | 5,000 | 100,000 |
| A | B | C | D | |
| ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача) | ||||
| Объем сырья: | ||||
| Этап | Коэфф. потерь | Объем потерь | Объем продукта на выходе | |
| 0,05 | =B4*C2 | =C2–C4 | ||
| 0,11 | =B5*D4 | =D4–C5 | ||
| 0,02 | =B6*D5 | =D5–C6 | ||
| ПРОДУКТОВЫЙ РАСЧЕТ (обратная задача) | ||||
| Объем продукта: | 82,859 | |||
| Этап | Коэфф. потерь | Объем потерь | Объем продукта на входе | |
| 0,02 | =C9*B11/(1–B11) | =C9+C11 | ||
| 0,11 | =D11*B12/(1–B12) | =D11+C12 | ||
| 0,05 | =D12*B13/(1–B13) | =D12+C13 |
Рис. 5.9в Рис. 5.9г
В случае, если речь идет об изъятии продукта, элементы в столбце В вводятся со знаком минус. Аналогичным образом строятся формулы для остальных этапов.
Хотя приведенный выше расчет рассматривался именно как продуктовый, очевидно, подобные же технологические (и не технологические) процессы существуют и в других отраслях производства и коммерческой деятельности.
| A | B | C | D | Е | D | Е | ||
| ПРОДУКТОВЫЙ РАСЧЕТ (прямая задача) | ||||||||
| Объем сырья: | ||||||||
| Этап | Доп. сырье | Коэф. потерь | Объем потерь | Объем на выходе | Объем потерь | Объем на выходе | ||
| 1% | 0,05 | 5,050 | 95,950 | =C4*C2*(1+B4) | =C2*(1+B4)–D4 | |||
| 30% | 0,11 | 13,721 | 111,014 | =C5*E4*(1+B5) | =E4*(1+B5)–D5 | |||
| 20% | 0,02 | 2,664 | 130,553 | Рис. 5.10 | =C6*E5*(1+B6) | =E5*(1+B6)–D6 |
| A | B | C | D | E | F | G | H | |
| Работники | Оценки | Всего КТУ | КТУ | КТУ1 | ||||
| Петр | 0,90 | 0,70 | 0,70 | 0,90 | 3,20 | 0,277 | 0,98 | |
| Иван | 0,60 | 0,55 | 0,60 | 0,40 | 2,15 | 0,186 | 0,66 | |
| Олег | 0,80 | 0,80 | 0,55 | 0,80 | 2,95 | 0,255 | 0,91 | |
| Вера | 0,90 | 0,90 | 0,45 | 1,00 | 3,25 | 0,281 | 1,00 | |
| Сумма | 11,55 | |||||||
| Рис. | 5.11 |
Пример 5.11. Определение коэффициента трудового участия (КТУ). На таком производстве, где невозможно оценить индивидуальное количество труда, принято по итогам месяца/недели оценивать его при помощи КТУ, которое в дальнейшем влияет на оплату. Чтобы исключить необъективность оценок, все члены бригады анонимно заполняет анкету, где выставляет КТУ (например, в диапазоне от 0 до 1) для каждого из своих коллег. Необходимо как-то обработать эти данные и сформировать обобщенные значения КТУ. На рисунке в колонках В:Е зафиксированы оценки для каждого из четырех членов бригады, в F они просуммированы, в G – вычисляется собственно КТУ
КТУ_работника=Всего_КТУ_работника/Сумма_КТУ_бригады.
Эти значения (в таблице колонка G) уже можно использовать для оценки результатов труда, однако более удобно, если они находятся в том же диапазоне, что и исходные оценки, т.е. в диапазоне от 0 до 1. Назовем его КТУ1 (столбец Н)
КТУ1_работника=КТУ_работника/МАКС(КТУ_всех_работников).
Рабочие формулы для первого работника приведены ниже
F2=СУММ(B2:E2), F6=СУММ(F2:F5), G2=F2/F$6, H2=G2/МАКС(G$2:G$5).
| A | B | C | D | E | F | |
| Весовые коэффициенты | ||||||
| Упаковка | Цвет | Консистенция | Вкус | |||
| 0,7 | 1,5 | |||||
| ЭКСПЕРТНЫЕ ОЦЕНКИ | ||||||
| Оценки | Упаковка | Цвет | Консистенция | Вкус | Итог | |
| Эксперт1 | ||||||
| Эксперт2 | ||||||
| Эксперт3 | ||||||
| Эксперт4 | ||||||
| Всего | 4,5 | 4,9 | 7,5 | 31,9 | ||
| Рис. | 5.12 |
Пример 5.12. Экспертная оценка качества. Похожая задача из совершенно иной сферы деятельности. Построим таблицу для экспертной оценки некоторого продукта. Рассматриваемый ниже подход используется в случае, когда нет четкого формального критерия анализа его качества (например качества вина). Здесь прибегают к услугам группы специалистов (экспертов), которые и оценивают продукт, исходя из своего опыта по нескольким параметрам. Для каждого из параметров они выставляют оценку по, например, десятибалльной шкале. При подведении итогов следует учесть разную значимость этих параметров. Очевидно, что значимость (весá) таких параметров, как вкус и цвет для пищевых продуктов существенно отличны (первый гораздо важнее). В виду этого для подсчета итоговой оценки вводится специальная нормативная таблица весовых коэффициентов (область В1:Е3) всех исследуемых параметров, которая также составляется экспертами для вин вообще. По каждому из параметров находится среднее арифметическое их оценок, причем, максимальная и минимальная оценки отбрасываются
B10=(СУММ(B6:B9)–МАКС(B6:B9)–МИН(B6:B9))*B3/2, C10=(СУММ(C6:C9)–МАКС(C6:C9)–МИН(C6:C9))*C3/2,
D10=(СУММ(D6:D9)–МАКС(D6:D9)–МИН(D6:D9))*D3/2, E10=(СУММ(E6:E9)–МАКС(E6:E9)–МИН(E6:E9))*E3/2.
Их сумма и даст интегральную оценку качества данного продукта, подвергшегося экспертизе (у нас 31,9 балла) F10=СУММ(B10:E10), на основании которой далее можно сравнивать между собой аналогичные продукты и принять решение об их дальнейшей коммерческой судьбе.
К оформлению таблицы. Здесь мы выделим жирным курсивным шрифтом для каждого из параметров оценки, не принимаемые в расчет (т.е. максимальные и минимальные значения). Для этого придется прибегнуть к условному форматированию клеток с оценками следующего вида (например для В6):
Условие 1 формула =ИЛИ(B6=МАКС(B$6:B$9);B6=МИН(B$6:B$9))
Пример 5.13. Расчет сдельной зарплаты. Построить таблицу вычисления сдельной (т.е. пропорциональной количеству произведенной продукции) зарплаты, а также налога и суммы на руки.
Зарплата работника определяется числом обработанных деталей, умноженным на стоимость обработки. Если работник допустил брак и испортил деталь, ее стоимость вычитается из заработка
зарплата=обработано_деталей*стоимость_работы – деталей_брака * стоимость_детали.
Таким образом, Зарплата Ивана будет определяться формулой D6=B6* C$2–C6*C$3. Полагаем, что налог исчисляется в зависимости от зарплаты: если она выше 5000 – налог составляет 20%, если нет – 13%.
Иными словами сумма_налога=зарплата*ЕСЛИ(зарплата >5000, то 13%, иначе 20%) или
E6=D6*ЕСЛИ(D6>=5000;F$1;C$1). Сумма на руки – F6=D6–E6. Итог по вертикали F9=СУММ(F6:F8).
| A | B | C | D | E | F | |
| Налог до: | 5000р | 13% | Налог от: | 5000р | 20% | |
| Стоимость | работы: | |||||
| Стоимость | детали: | |||||
| РАСЧЕТ ЗАРПЛАТЫ | ||||||
| Работник | Обработано деталей | Деталей брака | Зарплата | Сумма налога | Сумма на руки | |
| Петр | 1120,0 | 4480,0 | ||||
| Иван | 124,8 | 835,2 | ||||
| Олег | 540,8 | 3619,2 | ||||
| ВСЕГО | 2144,0 | 8934,4 | ||||
| Рис. | 5.13а |
Может случиться, что если брака окажется много, зарплата станет отрицательной (работник должен компенсировать нанесенный ущерб). В этом случае, конечно, никакой налог не удерживается и, следовательно, в формуле для налога следует предусмотреть выявление отрицательности заработка. С учетом вышесказанного уточним Е6






