Оценка запаса устойчивости может проводиться с помощью корневого и частотного показателей колебательности. Примем к рассмотрению способ оценки запаса устойчивости по распределению корней характеристического уравнения замкнутой системы, который позволяет легко и просто выполнить вычисления на ЭВМ, границы заданного запаса устойчивости в пространстве параметров настройки регулятора по соотношениям, получающиеся из условия:
(4.21)
где m — заданная степень колебательности;
При этом частота меняется в пределах от w =0 до w =p/Т, а из бесконечно большого числа решений уравнения выбирается только одно, соответствующее минимальному w. Подставив в выражение (4.21) формулы (4.20), (4.8) и с учетом (4.11), получим:
(4.22)
Введем обозначение: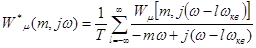 
. (4.23)
Тогда соотношение можно привести к виду:
. (4.24)
Комплексные функции переменной w в соотношении распишем в виде суммы действительной и мнимой частей:
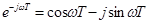(4.25)
; (4.26)
где: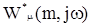 
, 
— модуль и фаза расширенной комплексной частотной характеристики эквивалентного дискретного объекта.
Записав полученное равенство в виде системы двух уравнений (одно — для действительной, другое — для мнимой части равенства), решим эту систему относительно параметров 
. Пространство параметров настройки цифрового ПИД‑регулятора четырехмерно. Задаваясь конкретными значениями параметров Т и 
, можно в плоскости параметров построить параметрическую кривую. Область, ограниченная этой кривой и прямыми 
и 
, является областью заданного запаса устойчивости для выбранных значений Т и .
Расчёт оптимальных настроек цифровых регуляторов осуществляется методом расширенных частотных характеристик и проводится в два этапа. На первом этапе производим расчёт и построение в плоскости параметров настроек регулятора линии равной степени колебательности (m=const), на втором этапе определяем в области заданного запаса устойчивости настройки регулятора, обеспечивающие наилучшее качество регулирования. Линия равной степени колебательности m=const строится в плоскости параметров определяемых по формулам:
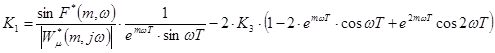(4.27)
(4.28)
3.4 Последовательность расчета оптимальных настроечных
параметров
Процесс расчета оптимальных настроечных параметров будет состоять из следующих этапов:
1. Задаемся значением периода квантования Т. Увеличение периода квантования ведет к ухудшению качества процесса регулирования. Однако, при очень малых Т улучшение качества достигается за счет существенного возрастания затрат на управление. Поэтому не следует выбирать период квантования слишком малым. Для нахождения приемлемого периода квантования можно использовать следующие рекомендации:
Т=0,01Т95¸0,1Т0, в нашем случае T=(0,039¸0,275) мин.
где Т95 ─ время достижения регулируемой координаты величины, равной 95% ее установившегося значения при действии на объект ступенчатого возмущения; Т0─ доминирующая постоянная времени объекта.
2. Задаемся значением параметра К3 = 0 и строим в плоскости параметров K1, К2 по уравнениям (33), (34) линию m = m3. При нахождении настроек примем m=0,366.
3. Примем в качестве оптимальных такие значения настроек ПИ- и ПИД‑регулятора, при которых система обладает запасом устойчивости не ниже заданного (m>mЗ) и коэффициент при интегральной составляющей в законе интегрирования имеет максимальную величину (
=max). Таким образом, для нахождения оптимальных настроек k1, k2, при заданных Т и достаточно определить точку максимума кривой равной степени колебательности m=mз.
4. По определённым оптимальным настройкам k1, k2 задаёмся значением параметра из диапазона: 
строим в плоскости параметров новую линию m=mЗ и определяем новые значения оптимальных настроечных параметров. Такой порядок нахождения значения коэффициента К3 связан с тем, что качество регулирования улучшается при увеличении К3 лишь до некоторого его критического значения. Дальнейшее увеличение К3 приводит к ухудшению качества регулирования.
5. Задаваясь рядом других значений периода квантования Т из диапазона Т=0,01Т95 ¸0,1Т0 определяем для них оптимальные настройки. Вычисление расширенной комплексной частотной характеристики эквивалентного объекта произведён по формуле:
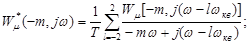(4.29)
Результаты расчета
Оптимальные настройки для каждого значения времени такта квантования выбирались на соответствующей линии m=0.221 и K2=max.
Рис.3.3 Области заданного запаса устойчивости при при Tkw=0,039 и различных значениях настроечного параметра К3
Рис.3.4 Области заданного запаса устойчивости при при Tkw=0,157 и различных значениях настроечного параметра К3
Рис. 3.6 Области заданного запаса устойчивости при при Tkw=0,275 и различных значениях настроечного параметра К3
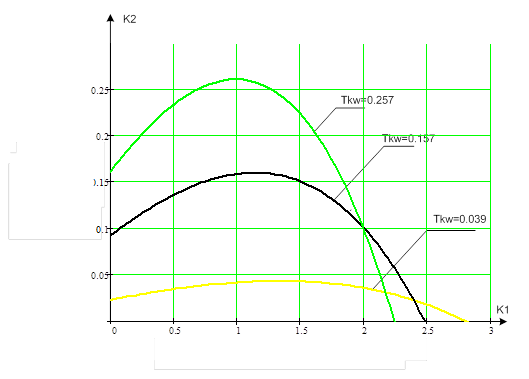
Рис. 3.5 Области заданного запаса устойчивости при K3=const и различных значениях времени такта квантования
4 Расчёт переходных процессов в цифровых АСР
Для синтеза АСР с заданными показателями качества работы необходимо построить переходные процессы для найденных параметров настройки регулятора и принять в качестве оптимальных те, при которых выполняются требования к качеству функционирования ЦАСР. Объект по каналу регулирования имеет передаточную функцию: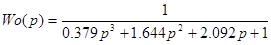 
.
По каналу возмущения передаточная функция объекта имеет вид:
.
Построим графики переходных процессов, которые будут происходить в системе, при различных возмущающих воздействиях: при изменении задания регулятора температуры на 0,5кг/см2, при изменении хода регулирующего органа на 20%. При построении графиков используем найденные настройки регулятора при различных значениях такта квантования.
Рис.4.1Переходный процесс при времени квантования Tkw=0,0143, разных К3 и изменении задания регулятору
Рис.4.2Переходный процесс при времени такта квантования Tkw=0,0143, разных К3 и изменении воздействия по каналу возмущения на 20%
Рис.4.3 Переходный процесс при времени квантования Tkw=0,0827, разных К3 и изменении задания регулятора
Рис.4.4Переходный процесс при времени такта квантования Tkw=0,0827, разных К3 и изменении воздействия по каналу возмущения на 20%
Рис.4.5 Переходный процесс при времени квантования Tkw=0,151, разных К3 и изменении задания регулятора.
Рис.4.6 Переходный процесс при времени такта квантования Tkw=0,151, разных К3 и изменении воздействия по каналу возмущения на 20%.
Результаты анализа переходных процессов в системе регулирования температуры сведем в таблицу 2.
Таблица 2 - Сводные данные по расчёту
| Настройки регулятора | Воздействия | ||||||||
| Tkw | к1 | к2 | к3 | U = 1 | FW = 20 | ||||
| Δθmах | Y | Тр | Δθmах | Y | Тр | ||||
| 0,0143 | 0,19 | 0,0044 | 0,46 | 0,33 | 0,57 | 0,8 | |||
| 0,234 | 0,0054 | 2,116 | 0,44 | 0,31 | 12,5 | 0,545 | 0,333 | ||
| 0,288 | 0,0065 | 4,232 | 0,42 | 0,29 | 0,525 | 0,2 | |||
| 0,0827 | 0,178 | 0,0243 | 0,45 | 0,33 | 0,573 | 1,12 | |||
| 0,215 | 0,029 | 0,325 | 0,42 | 0,29 | 0,55 | 0,62 | |||
| 0,233 | 0,0346 | 0,65 | 0,41 | 0,28 | 0,535 | 0,22 | |||
| 0,151 | 0,156 | 0,043 | 0,4 | 0,296 | 14,5 | 0,545 | 1,096 | ||
| 0,184 | 0,0487 | 0,1287 | 0,4 | 0,308 | 0,56 | 0,867 | |||
| 0,205 | 0,055 | 0,257 | 0,4 | 0,321 | 0,575 | 0,691 |
Выводы
Проанализировав результаты, приведенные в таблице 2, можно сделать следующий вывод:
За оптимальные настройки регулятора принимаем те настройки, которые обеспечивают заданное качество регулирования при возможно большем значении времени такта квантования TKw т.е. при наименьших затратах на управление.
Следовательно, в качестве оптимальных выбираем следующие значения настроенных параметров: K1 = 0,19; К2 = 0,0044; К3 = 0; Tkw=0,0143 мин. При этом динамическая ошибка регулирования Δθ mах =0,46, время регулирования Трег = 12. Степень затухания переходных процессов: по каналу управления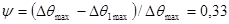 
, по каналу возмущения 
.
Остаточное отклонение регулируемого параметра, т.е. величина статической ошибки Δθ ст = 0. Итак, рассчитанная АСР удовлетворяет требуемым показателям качества работы: динамическая ошибка и время регулирования не превышает заданных (допустимых) значений. Степень затухания Yпереходных процессов близка к расчетной. Статическая ошибка регулирования при использовании ПИД - регулятора равна нулю.
Список литературы
1. Дудников Е.Г. Автоматическое управление в химической промышленности: Учебник для ВУЗов. – М.: Химия, 1987.
2. Ф.Шински. Системы автоматического регулирования химико-технологических процессов. Пер. с англ. М., “Химия”, 1974
3. Цифровая АСР. Пример выполнения расчета в дипломных проектах и методические указания. КГТУ, 2004.
4. Федоров Ю.Н. Основы построения АСУТП взрывоопасных производств. В 2-х томах. Т.1 «Методология». – М.: СИНТЕГ, 2006. – 720с.
