Свойства функции
- Постройте график функции. Укажите промежутки возрастания и убывания, а также точки экстремумов функции. а)
 ; б)
; б) 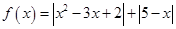 ; в)
; в) 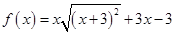 .
. - Исследовать свойства функции: а) Определите, является функция четной, нечетной или функцией общего вида 1)
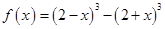 ; 2)
; 2) 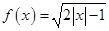 .
.
Б) Найти наибольшее и наименьшее значении функции: 1) 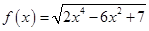 ; 2)
; 2)  , если
, если  .
.
Прогрессии
3. а) Сколько членов содержится в возрастающей арифметической прогрессии с положительными членами, е которой сумма членов с нечетными номерами относиться к сумме членов с четными номерами, как 7:6.
б) В геометрической прогрессии сумма первых трех членов равна 21, а сумма их квадратов – 169. Найдите первый член и знаменатель прогрессии.
В) Произведение пяти последовательных членов геометрической прогрессии равно 243. Найдите третий член прогрессии.
Г)Сумма первого, третьего и пятого членов убывающей арифметической прогрессии равна (-12), а их произведение равно 80. Найдите первый член и разность прогрессии.
Д)Найти первый член геометрической прогрессии, если известно, что ее знаменатель равен 3, а сумма шести первых членов равна 1820.
Е) Найти четыре числа, образующих знакочередующуюся геометрическую прогрессию, у которой второй член меньше первого на 35, а третий больше четвертого на 560.
Ж) Найти первый член и знаменатель бесконечной геометрической прогрессии, сумма которой равна 6, а сумма пяти первых членов равна (93/16).
З) Найдите первый член арифметической прогрессии, если ее разность равна 8, а сумма первых двадцати членов равна сумма следующих за ними десяти членов этой прогрессии.
И) В арифметической прогрессии 20 членов. Сумма членов, стоящих на четных местах, равна 250, а сумма членов, стоящих на нечетных местах, равна 220. Найти первый член и разность прогрессии.
К) Найти сумму шести членов ГП, если сумма первого и четвертого членов равна 35, а сумма второго и третьего членов равна 30. Известно, что прогрессия возрастающая.
Л) Найдите разность АП, если первый ее член равен 69, а сумма первых десяти членов равна сумме следующих за ними двадцати членов этой прогрессии.
М) В АП, состоящей из двадцати членов, сумма членов с четными номерами на 80 больше, чем сумма членов с нечетными номерами. Найдите разность прогрессии.
Н) В ГП, состоящей из тридцати членов, сумма членов с нечетными номерами в три раза меньше, чем сумма всех членов прогрессии. Найдите знаменатель прогрессии
Метод интервалов
4. Решите систему неравенств:
а) 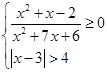 ; б)
; б)  ;
;
в)  ; г)
; г) 
Задачи с параметром
5. Решите уравнение: а)  ; б)
; б) 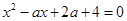 .
.
6. При каких значениях параметра а, сумма квадратов корней уравнения 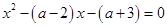 равна 9.
равна 9.
- Найдите все значения параметра с, при которых уравнение не имеет действительных корней
1) 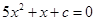 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
- Найдите все значения параметра а, при которых уравнение имеет два различных действительных корня:
1)  ; 2)
; 2) 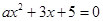 ; 3)
; 3)  ; 4)
; 4) 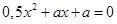 .
.
- При каких значениях параметра уравнение имеет равные корни?
1)  ; 2)
; 2) 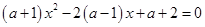 ; 3)
; 3)  ; 4)
; 4)  .\
.\
- Найдите все значения параметра, при которых оба корня уравнения лежат в промежутке (1;4).
- Найдите все значения параметра а, при которых 4 разделяет корни уравнения.






