1. Изобразить годограф вектор-функции r = cos t i + j + sin t к.
2. Найти производную функции z = x3 – 3x2y + 3xy2 + 1 в точке М1(3;1) в направлении, идущем от этой точки к точке М2(6;5).
3. Найти угол между градиентами функции z = (x2 + y2)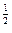 
в точках А(3;4) и (6;8).
4.Найти наибольшую крутизну подъёма поверхности z = ln(x2 + 4y2) точке Р(6;4;ln100).
5. Вычислить поверхностный интеграл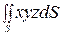 
, где x2 + y2 + z2 = R2/
6.Вычислить координаты центра тяжести части плоскости z = x, ограниченной плоскостями x + y = 1, y = 0 и x = 0, если поверхностная плотность F в каждой точке равна 1.
7.Найти поток векторного поля F = (2z – x) i +(x +2z) j +3z k через сторону треугольника S, вырезанного из плоскости x + 4y + z – 4 = 0 координатными плоскостями в том направлении нормали к плоскости, которая образует с осью Oz острый угол.
8.Найти циркуляцию вектора F = y i - x j + а k по окружности x = a cos t, y = a sin t, z = 0в положительном направлении.
9. Найти потенциал ньютоновского поля притяжения, если F = 
.
10. Тело вращается вокруг оси с постоянной угловой скоростью w. Найти вихрь скорости в произвольной точке тела.
11.Записать число z= 1+ 
i в тригонометрической форме.
12. На комплексной плоскости изобразить множество точек, задаваемое уравнением
z(t) = 
+ ti.
13. На комплексной плоскости задана прямая Im z= с, где с = const. Какое множество точек является её образом в отображении функцией w = z2?
14. Показать, что функция f(z) = z Re z дифференцируема во всех точках комплексной плоскости, но не является аналитической ни в одной точке этой плоскости.
15. Найти аналитическую функцию, у которой действительная часть равна
u(x,y) = ln(x2 + y2).
16. Вычислить интеграл 
, где L – отрезок прямой от т.Z1=0 до т.Z2= i.
17. Вычислить интеграл типа Коши
18. Разложить в ряд Тейлора функцию f(z) = sin z2 в окрестности точки z= 0.
19. Разложить в ряд Лорана функцию w = 
в кольце 1< 
< 2.
20. Вычислить: а) Ln(-1+3i); б) sin(1-2i); в) e -2 + i.
1. Записать число z= 1–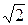 
i в тригонометрической форме.
2. На комплексной плоскости изобразить множество точек, задаваемое уравнением
z = 1 + i sin t, где 
.
3. На комплексной плоскости задана окружность =r, где r > 0. Какое множество точек является её образом в отображении функцией w =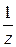 
?
4. Является ли функция f(z) = x 3+ y 3аналитической в каких-нибудь точках комплексной плоскости?
5. Найти аналитическую функцию, у которой действительная часть равна
u (x,y) = x 3 – 3 xy 2 + 2 xy.
6. Вычислить интеграл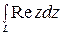 
, где L – отрезок прямой, соединяющий точки z1 = –1 + 2i и z2 = 0.
7. Вычислить интеграл типа Коши
8. Разложить в ряд Тейлора функцию f(z) = sin3 z в окрестности точки z = i.
9. Разложить в ряд Лорана функцию w = 
по степеням z -1.
10. Вычислить: а) 31+I; б) cos(1 + 2i); в) i Ln i.
11. Изобразить годограф вектор-функции: r = a cos t i + a sin t j + ct к.
12. Найти производную функции z = x2y2 – xy3 – 3y – 1 в точке М(2;1) в направлении, идущем от этой точки к началу координат.
13. Найти угол между градиентами функций z = (x2 + y2) 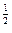и z = x –3y + 
в точке А(3;4).
14. Найти направление наибольшего возрастания функции z = ln(x2 + 4y2) в т. Р(6;4).
15. Вычислить поверхностный интеграл 
, где S – часть конической поверхности x2 + y2 = z2, заключённый между плоскостями z = 0 и z = 1.
16. Найти координаты центра тяжести чаcти поверхности z = 2 – x2 + y2 / 2, расположенной над плоскостью xOy, если поверхностная плотность равна 1.
17. Найти поток радиуса-вектора r = x i + y j + z k через замкнутую поверхность
z = 1 – (x2 + y2) 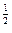, z = 0 (0 
.
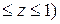18.Найти циркуляцию векторного поля F = (x + 3y + 2z) i + (2x +z) j + (x – y) k по контурутреугольника с вершинами в точках M(2; 0; 0), N(0; 3; 0), P(0; 0; 1).
19. Найти вихрь векторного поля, заданного вектором r = y2 i – x2 j + xz2 k.
20. Показать, что поле F = (2xy + 3y2 + 9y) i + (x2 + 6xy + 9x) j является потенциальным, и найти потенциал этого поля.
